提示

同学们，我们今天需要讲得极快.

旋度

$$\operatorname{curl}(P,Q,R)=\det\begin{pmatrix} \hat{i}&\hat{j}&\hat{k}\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ P&Q&R \end{pmatrix}=\nabla\times\vec{F}$$

我们可以把矢量场 $\vec{F}$ 看作一个风速场，问：绕某个轴 $\hat{n}$，旋转的快慢？

这时我们取一个平面垂直于 $\hat{n}$，轴与平面的交点记为中心点 $P$，可以计算某个探测质点在一圈之中受到风的做功：

$$\int_{\partial S}\vec{F}\cdot\text{d}\vec{r}\overset{\text{Stokes}}{=}\iint_S(\nabla\times\vec{F})\cdot\text{d}\vec{S}=\iint_S(\nabla\times\vec{F})\cdot\hat{n}\text{d}S$$

因为想要探测这一点处的旋转快慢，所以取积分区域趋于这一点的极限，这样 “测量” 得更加准确. 于是有

$$\begin{aligned} \lim_{r\to0}\frac{1}{\text{area}(S)}\int_{\partial S}\vec{F}\cdot\text{d}\vec{r}&=\lim_{r\to0}\frac{1}{\text{area}(S)}\iint_S(\text{curl}(\vec{F})\cdot\hat{n})\text{d}S\\\\ &=\lim_{r\to0}\text{curl}(\vec{F})_{Q}\cdot\hat{n}\\\\ &=(\operatorname{curl}\vec{F})(\vec{P})\cdot\hat{n} \end{aligned}$$

这说明，某点处的旋转快慢程度可以用该点处旋度向旋转轴的的投影来描述.

总结一下我们目前的场论知识：

$$\{\text{scalar field }A\}\overset{\text{grad}}{\longrightarrow}\{\text{vector field }\mathscr{X}\}\overset{\text{curl}}{\longrightarrow}\{\text{vector field}\}\overset{\text{div}}{\longrightarrow}\{\text{scalar field}\}\\\newline \Omega^0(\R^3)\overset{\text{d}}{\longrightarrow}\Omega^1(\R^3)\overset{\text{d}}{\longrightarrow}\Omega^2(\R^3)\overset{\text{d}}{\longrightarrow}\Omega^3(\R^3)$$

物理上有一些常用的命题：就是上述任意两步连续进行都会变成 $0$.

/Claim/

$$\operatorname{curl}(\operatorname{grad}\varphi)=0\,,\quad\operatorname{div}(\operatorname{curl}v)=0$$

梯度场无旋，旋度场无散.

上述图表是交换的，如下：

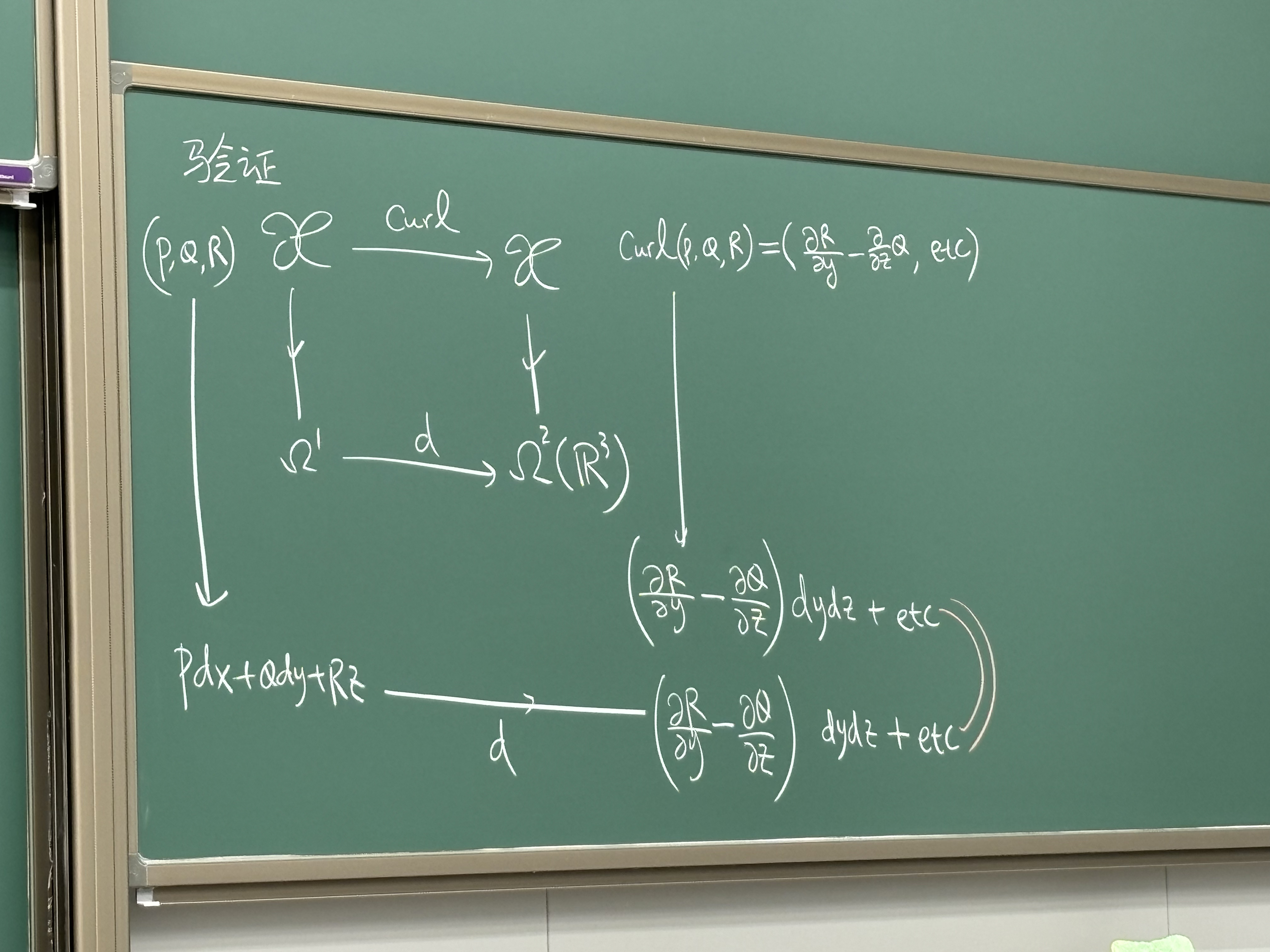
/Claim/

$\text{d}\circ\text{d}$ 恒为零.

/Proof/

$$\begin{aligned} &\text{d}\circ\text{d}(f\text{d}x_{i_1}\cdots\text{d}x_{i_k})\\\\ &=\text{d}\left(\sum_{j}\frac{\partial f}{\partial x_j}\text{d}x_j\text{d}x_{i_1}\cdots\text{d}x_{i_k}\right)\\\\ &=\sum_j\sum_t\frac{\partial}{\partial x_t}\left(\frac{\partial f}{\partial x_j}\right)\text{d}x_t\text{d}x_j\text{d}x_{i_1}\cdots\text{d}x_{i_k} \end{aligned}$$

计算 $\text{d}x_p\text{d}x_q\text{d}x_{i_1}\cdots\text{d}x_{i_k}$ 项的系数：

$$\frac{\partial}{\partial x_p}\left(\frac{\partial f}{\partial x_q}\right)-\frac{\partial}{\partial x_q}\left(\frac{\partial f}{\partial x_p}\right)=0$$

所以上式恒为零.

改述命题为：若 $\alpha=\text{d}\omega$，则 $\text{d}\alpha=0$. 我们想要问这个条件是否是充要条件，也就是是否有：若 $\text{d}\alpha=0$，则 $\alpha=\text{d}\omega$？

/Lemma/ (Poincare 引理)

在 $\R^n$ 上成立，设 $\alpha\in\Omega^k(\R^n)$ 满足 $\text{d}\alpha=0$，则 $\exist\,\,\omega\in\Omega^{k-1}(\R^n)$ 使得 $\alpha=\text{d}\omega$.

$n=3$ 时，物理上我们有这样的说法：

• $k=1$，$\R^3$ 上的无旋场一定有势 (若 $\nabla\times\vec{A}=0\Longrightarrow\exist\,\,\vec{A}=\nabla\varphi$)；
• $k=2$，$\R^3$ 上的无散场来自旋度场 (若 $\nabla\cdot\vec{B}=0\Longrightarrow\exist\,\,\vec{A}$ 使得 $\vec{B}=\nabla\times\vec{A}$).

我们不仔细证明这一结论，因为一般情况比我们想象中要难证明很多. 但是可以先尝试证明 $n=3$，$k=1$ 的情况：

/Proof/

设 $\vec{A}$ 无旋，来定义势能 $\varphi$. 定义：

$$\varphi(\vec{u})-\varphi(\vec{u}_0)=\int_{\vec{L}}\vec{A}\cdot\text{d}\vec{r}$$

验证定义与 $\vec{L}$ 无关：取简单闭曲线 $C=\vec{L}-\vec{L}'$ (不妨假设 $L$ & $L'$ 无自交点)

由 topology，可以证明任意简单闭曲线都能表示为某个曲面的边界. 则有

$$\int_C\vec{A}\cdot\text{d}\vec{r}=\iint_S(\nabla\times\vec{A})\cdot\text{d}\vec{S}=0$$

($\vec{A}$ 无旋) 所以

$$\int_{\vec{L}}\vec{A}\cdot\text{d}\vec{r}-\int_{\vec{L}'}\vec{A}\cdot\text{d}\vec{r}=0$$

得证.

对于 $k=2$ 的部分，Poincare 手动构造出了旋度场使得 $\nabla\times\vec{A}=\vec{B}$：

/Proof/

如下构造：

$$\begin{aligned} A_1(x,y,z)&=\int_0^1[zB_2(tx,ty,tz)-yB_3(tx,ty,tz)]t\text{d}t\\ A_2(x,y,z)&=\int_0^1[xB_3(tx,ty,tz)-zB_1(tx,ty,tz)]t\text{d}t\\ A_3(x,y,z)&=\int_0^1[yB_1(tx,ty,tz)-xB_2(tx,ty,tz)]t\text{d}t \end{aligned}$$

只需要证明 $\nabla\times\vec{A}=\vec{B}$. 我们只证明如下式子：

$$B_1(x,y,z)=\frac{\partial}{\partial y}A_3-\frac{\partial}{\partial z}A_2$$

我们在这里需要知道含参积分的求导：

对于含参积分

$$F(x)=\int_c^df(x,y)\text{d}y$$

/Theorem/

若 $f$ 是连续二元函数 $\Longrightarrow$ $F$ 连续.

进一步，若 $\frac{\partial f}{\partial x}$ 也连续，则

$$F'(x)=\int_c^d\frac{\partial f}{\partial x}(x,y)\text{d}y$$

提示

也就是 “积分里面求微分”.

Feynman 声称他在中学时知道了这个 “积分里求微分” 的方法，并且他吹嘘说这个方法让他得了 Nobel Prize，因为在做 QED 的路径积分时要非常经常地使用这一方法.

$$\begin{aligned} &\frac{\partial A_3}{\partial y}\\&=\frac{\partial}{\partial y}\int_0^1(yB_1-xB_2)t\text{d}t\\\\ &=\int_0^1\left[B_1(tx,ty,tz)+t\frac{\partial B_1}{\partial y}(tx,ty,tz)t-x\frac{\partial B_2}{\partial y}(tx,ty,tz)t\right]t\text{d}t \end{aligned}$$

另一项同理，相减得到

$$\begin{aligned} &\frac{\partial A_3}{\partial y}-\frac{\partial A_2}{\partial z}\\ &=\int_0^1\left[B_1+y\frac{\partial B_1}{\partial y}t-x\frac{\partial B_2}{\partial y}t-x\frac{\partial B_1}{\partial z}t+B_1+z\frac{\partial B_1}{\partial z}t\right]t\text{d}t\\\\ &=\int_0^1\left[2B_1+y\frac{\partial B_1}{\partial y}t+x\frac{\partial B_1}{\partial x}t+z\frac{\partial B_1}{\partial z}t\right]t\text{d}t\\\\ &=\int_0^1\left[2B_1(tx,ty,tz)t\text{d}t+\left(\frac{\text{d}B_1(tx,ty,tz)}{\text{d}t}\right)t^2\text{d}t\right]\\\\ &=\int_0^12B_1(tx,ty,tz)t\text{d}t+B_1(tx,ty,tz)t^2|^1_0-\int_0^1B_1(tx,ty,tz)\cdot2t\text{d}t\\\\ &=B_1(x,y,z) \end{aligned}$$

得证.

/Remark/

这是如何构造出来的？

相当于构造 $\Phi:\R^n\times[0,1]\to\R^n$，得到 $\Phi(x_1,\cdots,x_n,t)=(tx_1,\cdots,tx_n)$.

Poincare 令：

$$\int_0^1(\Phi^*\alpha)=\omega$$

则 $\omega\in\Omega^{k-1}(\R^n)$，容易验证 $\text{d}\omega=\alpha$.

Poincare 引理只在 $\R^n$ 上成立，对于一般的流形 $X$，

$$\Omega^0(X)\overset{\text{d}}{\longrightarrow}\Omega^1(X)\overset{\text{d}}{\longrightarrow}\Omega^2(X)\overset{\text{d}}{\longrightarrow}\cdots$$

问：还有没有 Poincare 引理成立？

我们已经证明 $\{\alpha=\text{d}\omega\}\subseteq\{\text{d}\alpha=0\}$，定义：

$$H^k(X)=\frac{\{\text{d}\alpha=0\,,\,\alpha\in\Omega^k(X)\}}{\{\alpha=\text{d}\omega\,,\,\alpha\in\Omega^{k-1}(X)\}}$$

来描述两个集合的差异. 这就是 $X$ 的 $k$ 维上同调 (de Rham cohomology)

$H^1(X)=\{X$ 上的无旋场$\}/\{$有势场$\}$.

$H^2(X)=\{X$ 上的无散场$\}/\{$旋度场$\}$.

提示

推荐大家在暑假看一本书 From Calculus to Cohomology. 这是我们课程最好的一本后续读物.

ODE

Ordinary Differential Equation.

求解 ODE 实际上就是求 (所有) 的 $y=y(x)$ 使之满足一个有关 $y$ 和 $y$ 的高阶导数的方程.

$$F(y(x),y^{(1)}(x),\cdots,y^{(n)}(x))=0\,,\quad\forall x\in I$$

在 $I$ 上求 ODE 的所有解 / 通解.

方法或者目的是：去掉求导符号，积分 / 做 $n$ 次积分.

同学们大多数是物理背景，在物理中，我们会更关心演化的过程，一般而言我们得到的条件是

$$\begin{cases} F(y,y^{(1)},\cdots,y^{(n)})=0\\\\ y(x_0)=y_0\\\\ y^{(1)}(x_0)=y_1\\ \vdots\\ y^{(n-1)}(x_0)=y_{n-1} \end{cases}$$

这类问题被称为 Cauchy 问题 / ODE 初值问题.

初等方法

分离变量法解一阶 ODE：

一般而言，一阶 ODE 是形如 $F(x,y(x),y'(x))=0$ 的方程. 可分离变量的一阶 ODE 是其中可以改写为 $y'(x)=f(x)g(y)$ 的一类.

这一类方程可以写成：

$$\frac{\text{d}y}{\text{d}x}=f(x)g(y)\Longrightarrow \frac{\text{d}y}{g(y)}=f(x)\text{d}x$$

1. 若可以找出 $1/g(y)$ 的原函数 $G(y)$，有

   $$G(y)=\int\frac{\text{d}y}{g(y)}$$

2. 由链式法则，得到 $G(y(x))=f(x)$ 的原函数，所以

   $$G(y(x))=\int f(x)\text{d}x$$

上述说法太过于麻烦，形式化的改写是直接两边不定积分：

$$\int\frac{\text{d}y}{g(y)}=\int f(x)\text{d}x$$

对于 Cauchy 问题中的可分离变量一阶 ODE，多一个条件 $y(x_0)=y_0$，这时严格的解法是

$$\int_{y_0}^{y(x)}\frac{\text{d}y}{g(y)}\overset{y(x)=y}{=}\int_{x_0}^x\frac{y'(x)\text{d}x}{g(y(x))}=\int_{x_0}^xf(x)\text{d}x$$

更加形式化的改写是直接分离变量，然后两边定积分：

$$\int_{y_0}^{y(x)}\frac{\text{d}y}{g(y)}=\int_{x_0}^xf(x)\text{d}x$$

一阶线性 ODE

线性 ODE $\longleftrightarrow$ 方程关于 $y,y',\cdots,y^{(n)}$ 的线性式子.

一阶线性 ODE $\longleftrightarrow$ $y'(x)+P(x)y(x)=Q(x)$.

齐次线性 ODE $\longleftrightarrow$ $Q(x)=0$；反之则为非齐次的.

解法是：

(1) 解齐次 ODE：$y'+P(x)y=0$. 显然可以分离变量，得到\

$$\frac{\text{d}y}{y}=-P(x)\text{d}x$$

提示

同学们，我们休息一会.

一阵骚动

同学们，要不这样，我们不休息了.

上述分离变量积分得到

$$y=Ce^{-\int_{x_0}^xP(t)\text{d}t}$$

(2) 对于一般的一阶线性 ODE：

将齐次的解中的 $C$ 从数变为函数 —— 常数变易法

考虑：

$$y(x)=C(x)e^{-\int_{x_0}^xP(t)\text{d}t}$$

代入，得到

$$C'(x)e^{-\int_{x_0}^xP}+C(x)e^{-\int_{x_0}^xP}(-P)+PCe^{-\int_{x_0}^x}=Q$$

后面两项抵消.

提示

“抵消” 的 “抵” 字下面有没有这一点？

最终得到公式：

$$y(x)=\left(\int Q(x)e^{\int P(t)\text{d}t}\text{d}x+C\right)e^{-\int P(t)\text{d}t}$$

这个公式 / 方法将作为基石，之后用到：

Bernoulli 方程、全微分方程 (积分因子法)、可降阶的 ODE、二阶 ODE (不显含 $y$ / 不显含 $x$)…

不显含时间的二阶微分方程

形如如下的方程：

$$\begin{cases} y''=H(y,y')\\\\ y(x_0)=y_0\\\\ y'(x_0)=y_1 \end{cases}$$

不显含 $x$. 求解的方法是做如下的映射：

$$\R\overset{y^{-1}}{\longrightarrow}I\overset{y'}{\longrightarrow}\R$$

其中 $I$ 是 $x$ 的定义域.

为了确认反函数的存在，要使用反函数定理，若 $y'(x_0)=y_1\neq0$，则在 $x_0$ 附近有反函数 $y^{-1}$. 因为我们觉得 "$y$" 既代表点又代表函数，容易引起歧义，所以将函数写成 $\varphi(x)$.

令 $P(y)=\varphi'(\varphi^{-1}(y))$

现在的问题是：$\varphi''(\varphi^{-1}(y))=?$

链式法则，得到

$$\frac{\text{d}P}{\text{d}y}=\frac{\varphi''(\varphi^{-1}(y))}{\varphi'(\varphi^{-1}(y))}$$

所以

$$\varphi''(\varphi^{-1}(y))=\varphi'(\varphi^{-1}(y))\frac{\text{d}P}{\text{d}y}=P(y)\frac{\text{d}P}{\text{d}y}$$

于是可以求解方程，原来的方程写为

$$P(y)\frac{\text{d}P}{\text{d}y}=H(y,P(y))$$

是一个关于 $P(y)$ 的一阶 ODE.

总结解法：

令 $P(y)=y'\circ y^{-1}$，则

$$y''=P(y)\frac{\text{d}P}{\text{d}y}$$

从而方程 $y''=H(y,y')$ 变为：

$$\begin{cases} P(y)\frac{\text{d}P}{\text{d}y}=H(y,P(y))\\\\ P(y_0)=y_1 \end{cases}$$

一阶 ODE 短期解

一阶 ODE 初值问题的短期解是存在且唯一的.

$$\begin{cases} y'=f(x,y)\\\\ y(x_0)=y_0 \end{cases}\quad\overset{\text{integral}}{\Longleftrightarrow}\quad\int_{x_0}^xy'(x)\text{d}x=\int_{x_0}^xf(x,y(x))\text{d}x$$

变为一个这样的积分方程：

$$y(x)=y_0+\int_{x_0}^xf(t,y(t))\text{d}t$$

求解函数空间 $M=C([a,b])$ 上的解，积分方程 RHS 是 $M$ 上的一个算子 $\text{T}:M\to M$，$\forall\varphi\in M$ 定义 $\operatorname{T}\varphi\in M$ 为

$$(\operatorname{T}\varphi)(x)=y_0+\int_{x_0}^xf(t,\varphi(t))\text{d}t\,,\quad\forall x\in[a,b]$$

所以求解这个积分方程等价于找到 $\varphi(x)\in M$ 使得 $\varphi(x)=(\operatorname{T}\varphi)(x)$，也就是找到 $\operatorname{T}$ 这个映射的不动点.

用压缩映像定理：

• $M$ 上的度量写成：

  $$d(h,g)=\max_{x\in[a,b]}|h(x)-g(x)|\,,\quad\forall h,g\in M$$

  易证这个度量完备.

• $\operatorname{T}$ 是否压缩？

  $$\begin{aligned} &d(\operatorname{T}\varphi,\operatorname{T}\psi)\\\\ &=\max_{x}|\operatorname{T}\varphi(x)-\operatorname{T}\psi(x)|\\\\ &=\left|\int_{x_0}^x(f(t,\varphi(t))\text{d}t-f(t,\psi(t))\text{d}t)\right|\\\\ &\leq\int_{x_0}^x|f(t,\varphi(t))\text{d}t-f(t,\psi(t))|\text{d}t \end{aligned}$$

  这里用到所谓 Lipshitz 条件：

  /Definition/

  称 $f$ 在 $[a,b]\times[c,d]=I$ 上是 Lipshitz 的，若 $\exist$ 常数 $L$ 使得

  $$|f(x,y_1)-f(x,y_2)|\leq L|y_1-y_2|\,,\quad\forall(x,y_1),(x,y_2)\in I$$

  /Theorem/ (Picard - Lindelof 定理)

  设 $f$ 是连续的且 Lipshitz，则 $\exist\,\,h>0$ (可能很小)，使得

  $$\begin{cases} y'=f(x,y)\\\\ y(x_0)=y_0 \end{cases}$$

  在 $[x_0-h,x_0+h]$ 上有唯一解 (短期解).

高阶线性 ODE

形如下面的 ODE：

$$y^{(n)}+a_{n-1}(x)y^{(n-1)}+\cdots+a_0(x)y(x)=b(x)\tag{*}$$

/Theorem/ (线性 ODE 有唯一长期解)

设 $a_i(x)\in C([a,b])$，$\forall i$.

则 Cauchy 问题：

$$\begin{cases} (*)\\\\ y(x_0)=y_0\\ \vdots\\ y^{(n-1)}(x_0)=y_{n-1} \end{cases}$$

有唯一解.

其理由是线性的一阶 ODE 就已经可以写下唯一的长期解 (常数变易法).

高阶线性 ODE $\longleftrightarrow$ 一阶线性 ODE 的矢量值版本. 引入：

$$v_1(x)=y(x)\,,\quad v_2(x)=y'(x)\,,\quad\cdots\,,\quad v_n(x)=y^{(n-1)}(x)$$

得到

$$\begin{pmatrix} v_1\\\vdots\\v_n \end{pmatrix}'=\begin{pmatrix} 0&1&\cdots\\ 0&0&1&\cdots\\ \vdots\\ 0&\cdots&&0&1\\ -a_0&-a_1&\cdots&&-a_n \end{pmatrix}+\begin{pmatrix} 0\\\vdots\\0\\v(x) \end{pmatrix}$$

常系数高阶线性 ODE

/Theorem/

齐次线性常系数方程：

$$y^{(n)}+a_{n-1}y^{(n-1)}+\cdots+a_0y=0$$

的全体解可由 $n$ 个线性无关解 (基本解生成).

提示

实际上这个时候已经下课了.

/Claim/

非齐次方程：

$$y^{(n)}+a_{n-1}y^{(n-1)}+\cdots+a_0y=b$$

的全体解 $=$ 自身特解 + 齐次方程通解.

我们的任务是证明：

• 齐次方程，求解 $n$ 个线性无关解；
• 非齐次方程的特解.

(1) 对于二阶齐次线性方程：

$$y''+py'+q=0$$

古人试出来：$y(x)=e^{\lambda t}$，代入得到特征方程 $\lambda^2+p\lambda+q=0$，特征根是 $\lambda=\alpha,\beta$. 所以这时候的解是

$$\phi_1(x)=e^{\alpha x}\,,\quad\phi_2(x)=e^{\beta x}$$

如果 $\alpha=\beta$ 的特殊情况，则通解为 (由 L'Hopital 法则给出) $xe^{\alpha x}$.

此时这两个解的线性组合生成全部的解，所以是通解.

(2) 对于二阶非齐次线性方程：

$$y''+py'+q=b$$

要找到一个特解，我们使用常数变易法，将 $c_1\phi_1(x)+c_2\phi_2(x)$ 中的两个常数 $c_1,c_2$ 变为函数 $c_1(x),c_2(x)$，但是这样会使得求导之后的项数越来越多，所以我们预先规定：

$c_1'\phi_1+c_2'\phi_2=0$. 同时要求 $c_1'\phi_1'+c_2'\phi_2'=b(x)$.

也就得到线性的方程组：

$$\begin{pmatrix} \phi_1&\phi_2\\\phi_1'&\phi_2' \end{pmatrix}\begin{pmatrix} c_1'\\c_2' \end{pmatrix}=\begin{pmatrix} 0\\b(x) \end{pmatrix}$$

特解将得到：

$$\begin{pmatrix} c_1'\\c_2' \end{pmatrix}=\frac{1}{\phi_1\phi_2'-\phi_2\phi_1'}\begin{pmatrix} \phi_2'&-\phi_2\\-\phi_1'&\phi_1 \end{pmatrix}\begin{pmatrix} 0\\b(x) \end{pmatrix}$$

更新日志

2025/10/9 02:50

查看所有更新日志

• f85b5-build(theme): update theme to rc-168于 2025/10/9
• e4956-fix(knowledge): add image于 2025/6/6
• 36aa0-feat(note): add integral note lesson-61于 2025/6/6

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)

贡献者: physnya

上一页Lesson 60 微分形式 & 场论