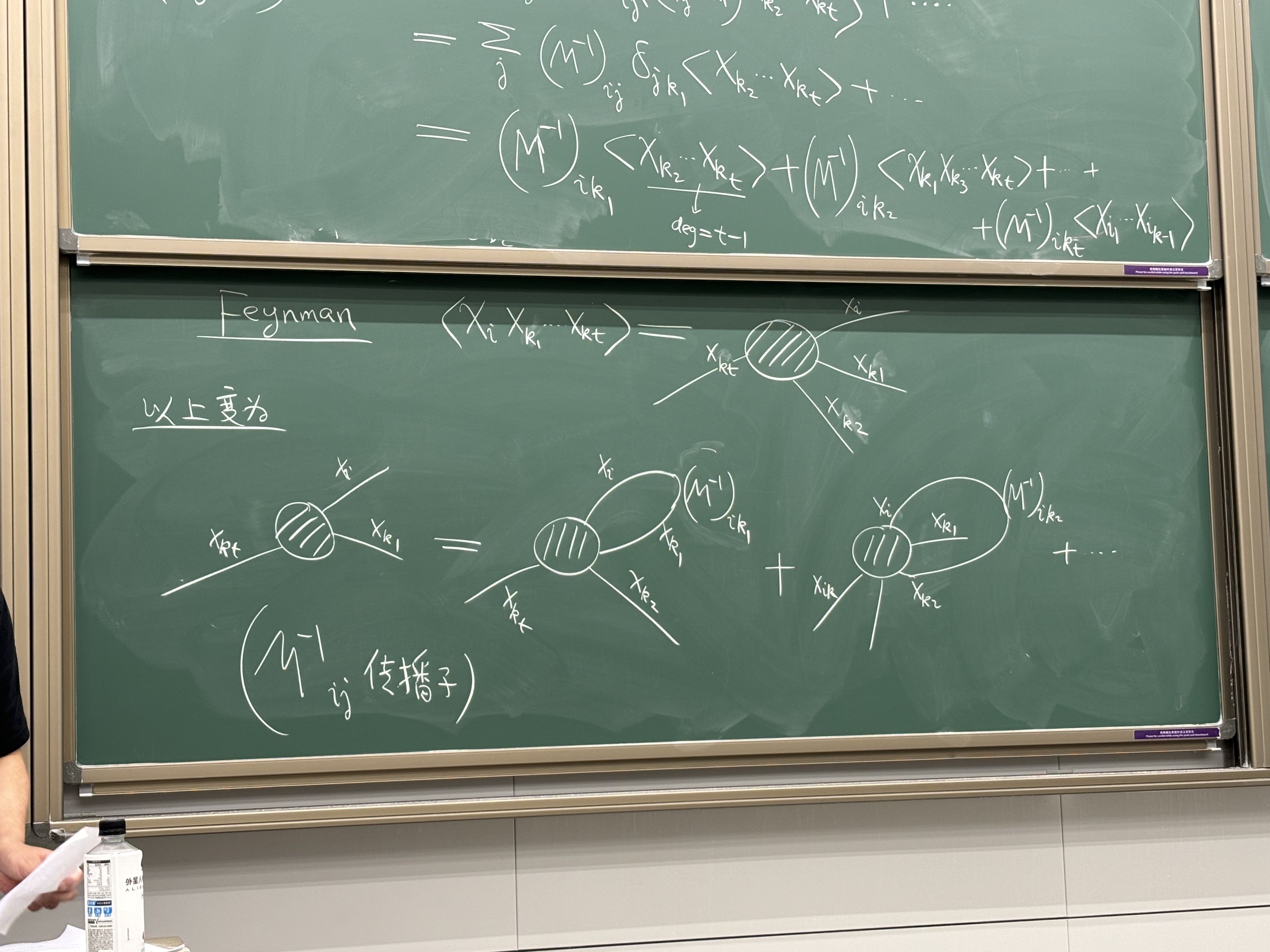Green 公式的应用

比如复变函数中的 Cauchy 积分公式 & 留数定理.

往年我们时间充裕的话会证明这一结论 (那你今年时间不充裕，就连微分方程都不讲了吗？！)

我们下面来证明这样的定理：

/Theorem/ (Brouwer 不动点定理)

设 $f:D\to D$ ($D=\{x^2+y^2\leq1\}$，也就是 $D=\{z\in\mathbb{C},|z|\leq1\}$) 是 $C^2$ 光滑的，则 $f$ 必有不动点.

/Proof/

反证法，设 $\forall z\in D$，$f(z)\neq z$. (衡量 $f(z)$ 与 $z$ 的差异，在一元情况下我们引入一个差函数，在高维情况可以引入一个差向量).

定义：$g(z)=($射线 $\overrightarrow{f(z)\to z}$ 与 $\partial D$ 的唯一交点$)$. 由 $f(z)\in C^2$，可知 $g(z)\in C^2$，得到 $g:D\to\partial D$ 是 $C^2$ 的，且 $\forall z\in\partial D$ 有 $g(z)=z$.

若 $g(z)$ 存在，则记 $g(x,y)=(u(x,y),v(x,y))\in S^1$，回忆 Gauss 曲线积分：

$$\int_C\frac{-v\text{d}u+u\text{d}v}{u^2+v^2}=\left\{\begin{array}{ll} 0&(0,0)\text{ in }C\\\\ 2\pi&(0,0)\text{ out of }C \end{array}\right.$$

(这个积分可以用来让人工智能判断复杂曲线和原点的位置关系)

把 $(u,v)$ 平面的 1 - form：

$$\omega=\frac{-v\text{d}u+u\text{d}v}{u^2+v^2}$$

通过 $g$ 拉回 (pull back) $x$ - $y$ 平面，得到 $g^*\omega$，再对其在 $\partial D$ 上积分.

/Definition/

$$\begin{aligned} g^*(\text{d}u)&=\frac{\partial u}{\partial x}\text{d}x+\frac{\partial u}{\partial y}\text{d}y\\ g^*(\text{d}v)&=\frac{\partial v}{\partial x}\text{d}x+\frac{\partial v}{\partial y}\text{d}y \end{aligned}$$

按照上述定义进行计算，得到拉回：

$$g^*(\omega)=\frac{-v(u_x\text{d}x+u_y\text{d}y)+u(v_x\text{d}x+v_y\text{d}y)}{u^2+v^2}$$

所以原来的 Gauss 积分为

$$\begin{aligned} I&=\int_{\partial D^+}g^*(\omega)\\\\ &=\int_{\partial D^+}\frac{(-vu_x+uv_x)\text{d}x+(-vu_y+uv_y)\text{d}y}{u^2+v^2}\\\\ &\overset{\text{Green}}{=}\iint_D\left[\frac{\partial}{\partial x}\left(\frac{-vu_y+uv_y}{u^2+v^2}\right)-\frac{\partial}{\partial y}\left(\frac{-vu_x+uv_x}{u^2+v^2}\right)\right] \end{aligned}$$

易证恒为零.

/Remark/

补充对 pull back 积分的一些说明：这其实是第二型曲线积分的换元公式.

设 $g:C_1\to C_2$ 是 $C^1$ 的双射，$C_1$ 已经定向，取一个符合 $C_1$ 定向的参数化，由 $g$ 映射到 $C_2$，得到对应的一个参数化，则这个参数化所确定的 $C_2$ 定向是等价于原来的 $C_1$ 定向的.

对于任何 $\omega=P\text{d}u+Q\text{d}v$ 有

$$A=\int_{C_2^+}g^*(\omega)=\int_{C_1^+}\omega$$

但是在未拉回的原来空间，计算

$$I'=\int\frac{-v\text{d}u+u\text{d}v}{u^2+v^2}=2\pi$$

我们知道 $I$ 和 $I'$ 等价，但是这里出现了矛盾，所以原假设不成立. 证毕.

/Example/

提示

我们上学期曾经吹嘘过，这学期我们将能够证明 “人为什么有发旋”.

/Definition/ (发旋)

头皮上的某处无法长出头皮切方向的头发，否则会违背和其他头发的连续性. 当然，可以长出沿头皮法方向的头发.

反证法，设无发旋. 因为我们的定义只和切向有关，所以我们只考虑切向的问题.

定义：$g(\vec{x})=\vec{x}$ 处头发向量向 $\text{T}_xB$ 的投影 ($\forall\vec{x}\in B$). 注意到 $B$ 和闭圆盘 $D=\{|z|\leq1\}$ 是微分同胚的，我们的假设可以翻译为：不存在 $g(\vec{x})$ 为零的点.

可以将 $g$ 视为 $g:D\to\R^2|\vec{0}$. 如果再做一次归一化，就会得到这个命题和上面我们刚刚证明的结论等价，即 $\exist g(z)$，$\forall z\in\partial D$，$g(z)=z$. 这样的 $g$ 是不存在的，所以 “人必须有发旋”.

Gauss 公式

Green 公式是

$$\int_{\partial D}P\text{d}x+Q\text{d}y=\iint_D\Box$$

是将 1 维变成 2 维. Gauss 公式则是

$$\iint_{\partial Q}P\text{d}y\text{d}z+Q\text{d}z\text{d}x+R\text{d}x\text{d}y=\iiint_Q\Box$$

是将 2 维变成 3 维.

对于 Gauss 公式，我们也要给出 local model，考虑一个上下底面为曲面的曲边柱体，定义指向柱体外部为定向.

计算：

$$\begin{aligned} &\iint_{\partial V}R\text{d}x\text{d}y\\\\ &=\iint_{S_1}+\iint_{S_2}+\iint_{S_3}\\\\ &=-\iint_DR(x,y,z_1(x,y))\text{d}x\text{d}y+\iint_DR(x,y,z_2(x,y))\text{d}x\text{d}y+0 \end{aligned}$$

其中侧面 $S_3$ 的积分是为零的. 接下来得到

$$\begin{aligned} &=\iint_D(R(x,y,z_2(x,y))-R(x,y,z_1(x,y)))\text{d}x\text{d}y\\\\ &=\iint\text{d}x\text{d}y\left(\int_{z_1(x,y)}^{z_2(x,y)}\frac{\partial R}{\partial z}(x,y,z)\text{d}z\right)\,,\quad\text{need }\frac{\partial R}{\partial z}\in C(V)\\\\ &\overset{\text{Fubini}}{=}\iiint_V\frac{\partial R}{\partial z}\text{d}(\mathcal{Vol}) \end{aligned}$$

对于一般的三维区域，可以分割成多个 local model，得到 $\Omega=\underset{i}{\bigcup}V_i$，有

$$\iint_{\partial\Omega^+}R\text{d}x\text{d}y=\sum_{i}\iint_{\partial\Omega_i^+}R\text{d}x\text{d}y=\sum_i\iiint_{\Omega_i}\frac{\partial R}{\partial z}\text{d}\Omega=\iiint_{\Omega}\frac{\partial R}{\partial z}\text{d}\Omega$$

对于另外两个方向，也是使用 local model 并推广，最终得到 Gauss 公式：

/Theorem/

(和 Green 公式一样，我们希望加强这个定理的条件以满足对称性，所以本来的 $\partial P/\partial x$，$\partial Q/\partial y$，$\partial R/\partial z\in C(\Omega)$ 修改为下述条件)

设 $P,Q,R\in C^1(\Omega)$，则有

$$\iint_{\partial\Omega}P\text{d}y\text{d}z+Q\text{d}z\text{d}x+R\text{d}x\text{d}y=\iiint_\Omega\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)\text{d}\Omega$$

/Example/ (Gauss 静电场定理)

原点处点电荷产生的静电场可以写为

$$\vec{E}=\frac{1}{r^2}\frac{\vec{r}}{r}$$

分类讨论：

(1) 若 $\vec{0}\notin\Omega$，则

$$P=\frac{x}{(x^2+y^2+z^2)^{3/2}}\in C^1(\Omega)$$

其他分量同理. 所以可以计算

$$\begin{aligned} I&=\iiint_\Omega\frac{\partial}{\partial x}\left(\frac{x}{r^3}\right)+\frac{\partial}{\partial y}\left(\frac{y}{r^3}\right)+\frac{\partial}{\partial z}\left(\frac{z}{r^3}\right)\\\\ &=\iiint_\Omega\frac{3r^3-3r(x^2+y^2+z^2)}{r^6} \end{aligned}$$

(2) 若 $\vec{0}\in\Omega$，则在 $\Omega$ 中减去一个 $0$ 的邻域，然后分别计算内外两个面积分即可.

综上所述：

$$I=\left\{\begin{array}{ll} 0&\vec{0}\notin\Omega\\\\ 4\pi&\vec{0}\in\Omega \end{array}\right.$$

/Example/ (Gauss 积分)

如下积分：

$$\iiint_{\R^3}e^{-S(x,y,z)}\text{d}x\text{d}y\text{d}z$$

其中，

$$S(x,y,z)=\frac{1}{2}\sum_i\sum_jM_{ij}x_ix_j$$

($M$ 为正定矩阵)

我们的目标是求出某个观测量的平均值，也就是：

$$\braket{f}=\iiint_{\R^3}f\cdot e^{-S(x,y,z)}\text{d}x\text{d}y\text{d}z$$

---

对于无穷积分，要先截断再取极限. 有：

$$\begin{aligned} \lim_{R\to\infty}\iint_{S}fe^{-S}\text{d}S&=\lim\iiint_V\frac{\partial}{\partial x_i}(fe^{-S})\text{d}V\\\\ &=\iiint\left(\frac{\partial f}{\partial x_i}e^{-S}+fe^{-S}\left(-\frac{\partial S}{\partial x_i}\right)\right)\text{d}V\\\\ &=\braket{\frac{\partial f}{\partial x}}-\braket{f\frac{\partial S}{\partial x}} \end{aligned}$$

但是 LHS 是零，所以得到均值的一种计算：

$$\begin{aligned} \braket{\frac{\partial f}{\partial x_i}}&=\braket{f\frac{\partial S}{\partial x_i}}\\ &=\braket{f\sum_iM_{ij}x_j}\\ &=\sum_jM_{ij}\braket{fx_j} \end{aligned}$$

所以得到

$$\begin{pmatrix} \braket{\frac{\partial f}{\partial x_1}}\\ \vdots\\ \braket{\frac{\partial f}{\partial x_n}} \end{pmatrix}=(M)\begin{pmatrix} \braket{fx_1}\\ \vdots\\ \braket{fx_n} \end{pmatrix}$$

也就是所谓的 Wick Lemma：

$$\braket{x_if}=\sum_{j=1}^nM_{ij}^{-1}\braket{\frac{\partial f}{\partial x_j}}$$

其特例是若 $f=$ 单项式 $x_{k_1}\cdots x_{k_t}$，代入左边，得到

$$\begin{aligned} \braket{x_i\cdot x_{k_1}\cdots x_{k_t}}&=\sum_j(M^{-1})_{ij}\braket{\frac{\partial}{\partial x_j}(x_{k_1}\cdot x_{k_2}\cdots x_{k_t})}\\ &=\sum_j(M^{-1})_{ij}\delta_{jk_1}\braket{x_{k_2}\cdots x_{k_t}}+\cdots \end{aligned}$$

也就是变成少两个变量的所有平均值之和.

---

Feynman 图：

Stokes 公式

Green 公式是在一个二维空间中的曲面，如果在三维空间中的一个曲面，它上面的积分和边界上的积分有何关系？

进行一个参数化 $\Phi(u,v)=(x(u,v),y(u,v),z(u,v))$. 用这样的一个参数化将曲面 $D$ 映射到平面 $S$ 上.

先确定定向：对于 $\partial D$ 取一个参数化 $\Phi(\gamma(t))$，这是由 $\partial S$ 的参数化 $\gamma(t)$ 诱导的. 两个参数化所导致的定向是等价的. 下面计算某分量：

$$\begin{aligned} &\int_{\partial S}P\text{d}x\\\\ &=\int_{\partial D}Px_u\text{d}u+Px_v\text{d}v\\\\ &=\iint_D\Big[\left(\frac{\partial P}{\partial x}x_u+\frac{\partial P}{\partial y}y_u+\frac{\partial P}{\partial z}z_u\right)x_v+Px_{vu}\\ &\quad-\left(\frac{\partial P}{\partial x}x_v+\frac{\partial P}{\partial y}y_v+\frac{\partial P}{\partial z}z_v\right)x_u-Px_{uv}\Big]\text{d}u\text{d}v\\\\ &=\iint_D\left[\frac{\partial P}{\partial y}(-x_uy_v+x_vy_u)+\frac{\partial P}{\partial z}(z_ux_v-z_vx_u)\right]\text{d}u\text{d}v\\\\ &=\iint_D\det\begin{pmatrix} 0&\frac{\partial P}{\partial z}&-\frac{\partial P}{\partial y}\\ x_u&y_u&z_u\\ x_v&y_v&z_v \end{pmatrix}\text{d}u\text{d}v\\\\ &=\iint_S\frac{\partial P}{\partial z}\text{d}z\text{d}x-\frac{\partial P}{\partial y}\text{d}x\text{d}y \end{aligned}$$

另外的两个式子可以由轮换性 ($x,y,z$ 轮换，$P,Q,R$ 轮换) 得证.

/Theorem/ (Stokes 公式)

设 $P,Q,R\in C^1(S)$，则

$$\int_{\partial S}P\text{d}x+Q\text{d}y+R\text{d}z=\iint_S\det\begin{pmatrix} \text{d}y\text{d}z&\text{d}z\text{d}x&\text{d}x\text{d}y\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ P&Q&R \end{pmatrix}$$

对于这个积分的定向问题，我们理应再给出一个 30 min 的推导，但是时间似乎不够了. 简单说一下结论，就是右手螺旋法则.

---

警告

我们还差一点点没有讲，也就是 ODE. 下一次课我们可能会采用 PPT 的方式，请大家提前看完群里的去年讲课录像.

?????????

更新日志

2025/5/30 04:19

查看所有更新日志

• a6392-feat(note): add integral note于 2025/5/30

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)