菲兹克斯喵

外观

Lesson 58 Green 公式

约 1776 字大约 6 分钟

2025-5-28

Green 公式

local model：

∫∂DP(x,y)dx=∫abP(x,ϕ1(x))dx−∫abP(x,ϕ2(x))dx=−∫ab(P(x,ϕ2(x))−P(x,ϕ1(x)))dx=−∫ab(∫ϕ1(x)ϕ2(x)∂P∂y(x,y)dy)dx ,need ∂P∂y continuous=−∬D∂P∂ydA\begin{aligned} \int_{\partial D}P(x,y)\text{d}x&=\int_a^bP(x,\phi_1(x))\text{d}x-\int_a^bP(x,\phi_2(x))\text{d}x\\ &=-\int_a^b(P(x,\phi_2(x))-P(x,\phi_1(x)))\text{d}x\\ &=-\int_a^b\left(\int_{\phi_1(x)}^{\phi_2(x)}\frac{\partial P}{\partial y}(x,y)\text{d}y\right)\text{d}x\,,\quad\text{need }\frac{\partial P}{\partial y}\text{ continuous}\\ &=-\iint_D\frac{\partial P}{\partial y}\text{d}A \end{aligned}

也就是将一个两边为直线段的曲边四边形上的线积分化为另一个函数的面积分. 我们自然要问，能不能对任意的闭曲线、任意的平面区域 EE 做这样的变换？

/Definition/ (简单闭曲线)

Simple Closed Curve，无自交点的闭合连续曲线.

/Theorem/ (Jordan 曲线定理)

设 Γ\Gamma 是平面上的简单闭曲线，则 R2∣Γ\R^2|\Gamma 分成两个两个道路连通分支，其中一个分支是无边界的，称为外部，另一个分支是有边界的，称为内部.

进一步地，上述曲线 Γ\Gamma 的内部区域 DD 同胚于开圆盘 BB.

这个定理的证明是复杂的，要使用比较复杂的 topology.

称 (Γ(\Gamma 的内部 D)∪ΓD)\cup\Gamma 同胚于闭圆盘，为 Γ\Gamma 所围成的 (界定的) “拓扑圆盘” / 带边区域.

如果在 C0C_0 围成的拓扑圆盘 D0D_0 内，再在 D0D_0 内部画简单闭合曲线 C1,⋯ ,CnC_1,\cdots,C_n 得到一个新的区域：E=D0∣(⋃ni=1(CiE=D_0|(\underset{i=1}{\overset{n}{\bigcup}}(C_i 的内部))))，称为带了 nn 个洞的拓扑圆盘.

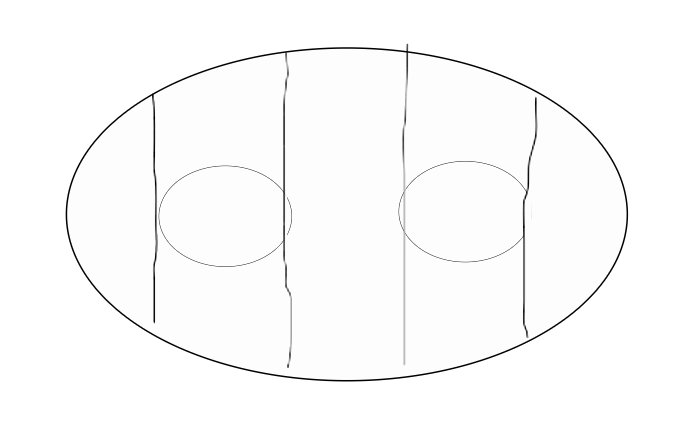
(第一次用 Inkscape 画得超级抽象请见谅)

推广公式到区域 EE：我们用竖直的线来分割这个区域，有时候穿过内部的 “洞”，就会导致交线出现突变点，将每一块加起来得到：

∑l∫EPdx=∑i∬Ei−∂P∂ydA\begin{aligned} \sum_l\int_EP\text{d}x&=\sum_i\iint_{E_i}-\frac{\partial P}{\partial y}\text{d}A \end{aligned}

对于每一块 EiE_i，其边界 ∂Ei\partial E_i 来源于本身的边界和我们所设定的直线段切痕，且积分方向均为逆时针绕转，那么我们可以将这些积分合成为外圈的一个大积分，和内部 “洞” 边界上的反向积分.

/Theorem/ (Green 公式)

设 EE 是任意的带 nn 个孔的拓扑圆盘，且 ∂P∂y\frac{\partial P}{\partial y} 在 EE 上连续，则

∫C0,+Pdx+∑i=1n∫Ci,−Pdx=−∬E∂P∂ydA\int_{C_0,+}P\text{d}x+\sum_{i=1}^n\int_{C_i,-}P\text{d}x=-\iint_E\frac{\partial P}{\partial y}\text{d}A

其中 "++" 为逆时针方向，"−-" 为顺时针方向.

/Definition/

对于 ∂E\partial E 定义 EE 的边界的正定向为：在边界上沿着定向方向运动时，EE 的总在左边.

也就是：EE 的最大边界为逆时针定向，各个 “洞” 的边界为顺时针定向.

在定义了如上的定向之后，我们的 Green 公式可以被改写成下述更加简洁的形式：

∫∂E+Pdx=−∬E∂P∂ydA\int_{\partial E^+}P\text{d}x=-\iint_E\frac{\partial P}{\partial y}\text{d}A

这时有同学会问，第二型积分中还有 QdyQ\text{d}y 项，在这样的时候 Green 公式怎么表达？我们限于时间不作重复的分割区间的工作，仅满足于计算一下 local model.

对于上下两边为直线段的曲边四边形，可以写出：

∫∂DQdy=∫cdQ(ϕ2(y),y)dy−∫cdQ(ϕ1(y),y)dy=∫cd(Q(ϕ2(y),y)−Q(ϕ1(y),y))dy=Newton - Leibniz∫cd(∫ϕ1(y)ϕ2(y)∂Q∂x(x,y)dx)dy=∬D∂Q∂xdA\begin{aligned} \int_{\partial D}Q\text{d}y&=\int_c^dQ(\phi_2(y),y)\text{d}y-\int_c^dQ(\phi_1(y),y)\text{d}y\\ &=\int_c^d(Q(\phi_2(y),y)-Q(\phi_1(y),y))\text{d}y\\ &\overset{\text{Newton - Leibniz}}{=}\int_c^d\left(\int_{\phi_1(y)}^{\phi_2(y)}\frac{\partial Q}{\partial x}(x,y)\text{d}x\right)\text{d}y\\ &=\iint_D\frac{\partial Q}{\partial x}\text{d}A \end{aligned}

如果和上面的条件写在一起，我们要求 ∂P∂y\frac{\partial P}{\partial y} 和 ∂Q∂x\frac{\partial Q}{\partial x} 连续，这在坐标的变换下并不是很对称，所以我们宁愿把定理放弱，加上一个更强的条件 P,Q∈C1(E)P,Q\in C^1(E). 可以写出如下的定理：

/Theorem/ (Green 公式)

设 P,Q∈C1(E)P,Q\in C^1(E)，则有

∫∂E+(Pdx+Qdy)=∬E(−∂P∂y+∂Q∂x)dxdy\int_{\partial E^+}(P\text{d}x+Q\text{d}y)=\iint_E\left(-\frac{\partial P}{\partial y}+\frac{\partial Q}{\partial x}\right)\text{d}x\text{d}y

有些人觉得这个公式不好记忆，那么我们用 Newton - Leibniz 公式形式化的写出：

∫∂E(Pdx+Qdy)=∫Ed(Pdx+Qdx)\int_{\partial E}(P\text{d}x+Q\text{d}y)=\int_E\text{d}(P\text{d}x+Q\text{d}x)

所以可以写出：

∂P∂xdxdx+∂P∂ydydx+∂Q∂xdxdy+∂Q∂ydydy=(−∂P∂y+∂Q∂x)dxdy\frac{\partial P}{\partial x}\text{d}x\text{d}x+\frac{\partial P}{\partial y}\text{d}y\text{d}x+\frac{\partial Q}{\partial x}\text{d}x\text{d}y+\frac{\partial Q}{\partial y}\text{d}y\text{d}y=\left(-\frac{\partial P}{\partial y}+\frac{\partial Q}{\partial x}\right)\text{d}x\text{d}y

这样可以写成所谓的微分形式：

{dxdx=dydy=0dxdy=−dydx\left\{\begin{array}{ll} \text{d}x\text{d}x=\text{d}y\text{d}y=0\\ \text{d}x\text{d}y=-\text{d}y\text{d}x \end{array}\right.

(？？？微分形式竟然是这样来的？)

/Example/ (面积)

可以用 Green 公式给出一种计算面积的方法：

area(D)=∬Edxdy\text{area}(D)=\iint_E\text{d}x\text{d}y

只要构造 −∂P∂y+∂Q∂x=1-\frac{\partial P}{\partial y}+\frac{\partial Q}{\partial x}=1 就能够将这个积分转化为曲线积分，可行的构造有：

Q=x ,P=0Q=0 ,P=−yQ=x2 ,P=−y2Q=x\,,\quad P=0\\ Q=0\,,\quad P=-y\\ Q=\frac{x}{2}\,,\quad P=-\frac{y}{2}

等等.

为什么要这么干呢？

有一个 “等周不等式”，就是在周长相等的时候围成最大的面积，这时就需要用边界来表示面积.

/Example/ (Green 对平面流体流量的公式)

二维流体，点 (x,y)(x,y) 处的流速 v⃗(x,y)=(v1,v2)\vec{v}(x,y)=(v_1,v_2).

单位时间内流出 CC 的流量 I=I= ？

显然这个流量可以定义为如下积分：

I=∫C(v⃗(x,y)⋅n^(x,y))dlI=\int_C(\vec{v}(x,y)\cdot\hat{n}(x,y))\text{d}l

考虑将 n^\hat{n} 逆时针转 90°90\degree，可以得到切矢量，经过计算得到

I=∫C(v1,v2)⋅(e2,−e1)dl=∫C(−v2dx+v1dy)\begin{aligned} I&=\int_C(v_1,v_2)\cdot(e_2,-e_1)\text{d}l\\ &=\int_C(-v_2\text{d}x+v_1\text{d}y) \end{aligned}

/Claim/

设 v⃗=(v1,v2)∈C1(D)\vec{v}=(v_1,v_2)\in C^1(D)，DD 是 CC 围成的区域，则

∫Cv⃗⋅n^dl=∬D(∂v1∂x+∂v2∂y)dxdy\int_C\vec{v}\cdot\hat{n}\text{d}l=\iint_D\left(\frac{\partial v_1}{\partial x}+\frac{\partial v_2}{\partial y}\right)\text{d}x\text{d}y

/Proof/

∫Cv⃗⋅n^dl=∫C(−v2dx+v1dy)=∬D(∂v1∂x+∂v2∂y)dxdy\begin{aligned} \int_C\vec{v}\cdot\hat{n}\text{d}l&=\int_C(-v_2\text{d}x+v_1\text{d}y)\\ &=\iint_D\left(\frac{\partial v_1}{\partial x}+\frac{\partial v_2}{\partial y}\right)\text{d}x\text{d}y \end{aligned}

(更快的方法是：

I=∫Cv⃗⋅n^dl=∫CR(v⃗)⋅R(n^)dl=∫C(−v2,v1)⋅e^dl=∫C(−v2dx+v1dy)\begin{aligned} I&=\int_C\vec{v}\cdot\hat{n}\text{d}l\\ &=\int_CR(\vec{v})\cdot R(\hat{n})\text{d}l\\ &=\int_C(-v_2,v_1)\cdot\hat{e}\text{d}l\\ &=\int_C(-v_2\text{d}x+v_1\text{d}y) \end{aligned}

其中 RR 是旋转 90°90\degree 的变换.

如果取 v⃗=∇u\vec{v}=\nabla u (是势能的 gradient)，则上述命题给出：

∫C∂u∂n^dl=∬D∇2udxdy\int_C\frac{\partial u}{\partial\hat{n}}\text{d}l=\iint_D\nabla^2u\text{d}x\text{d}y

如果觉得上述例子不够生动，我们还有 Gauss 计算无限长直导线产生的磁场的例子：

/Example/ (直导线磁场)

积分为

I=∫C−ydx+xdyx2+y2I=\int_C\frac{-y\text{d}x+x\text{d}y}{x^2+y^2}

其中 CC 为任意的一个闭合曲线.

I=∬D(∂∂y(yx2+y2)+∂∂x(xx2+y2))dxdy=0\begin{aligned} I&=\iint_D\left(\frac{\partial}{\partial y}\left(\frac{y}{x^2+y^2}\right)+\frac{\partial}{\partial x}\left(\frac{x}{x^2+y^2}\right)\right)\text{d}x\text{d}y=0 \end{aligned}

这和我们之前的结果不一样！

这是因为奇点在我们的区域内，这时不能使用 Green 公式.

更新日志

2025/5/28 07:12
查看所有更新日志
  • e4414-feat(note): add integral note于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)