Lesson 21 能带理论

约 660 字大约 2 分钟

2025-12-03

Bloch 定理：周期性波函数满足

\psi(x+a)=e^{\text{i}Ka}\psi(x)

其中这里的 $K$ 并不对应动能，而是晶格所代表的空间周期的体现.

证明是考虑 $Df(x)=f(x+a)$ ，利用势能的周期性 $V(x)=V(x+a)$ 来计算.

如果移动了 $n$ 个单元，那么 $\psi(x+Na)=e^{\text{i}K\cdot Na}\psi(x)$ ，周期性边界条件要求 $K\cdot Na=2\pi$ ，就能确定

K=\frac{2\pi n}{Na},\quad n\in\mathbb{Z}

在经典的极限下， $N\to\infty$ ，整个固体是连续的.

Dirac Comb (梳子)：考虑势能是在整点出现的 $\delta$ 函数，其他地方为零.

V(x)=\alpha\sum_{j=0}^N\delta(x-ja)

在每一个势阱位置， $\psi(x)=A\sin kx+B\cos kx$ ， $k=\sqrt{2mE/\hbar^2}$ . 连接点的条件是波函数连续、一阶导数相差一个特定值：

\psi(0^+)=\psi(0^-),\quad \psi'(0^+)-\psi'(0^-)=\frac{2m\alpha}{\hbar^2}\psi(0)

化简为 —— 色散关系：

\cos Ka=\cos ka+\frac{m\alpha}{\hbar^2k}\sin ka

定义两个无量纲参数，

z\equiv ka,\quad \beta\equiv\frac{m\alpha a}{\hbar^2}\Longrightarrow\cos Ka=f(z)=\cos z+\beta\frac{\sin z}{z}

方程如图所示，

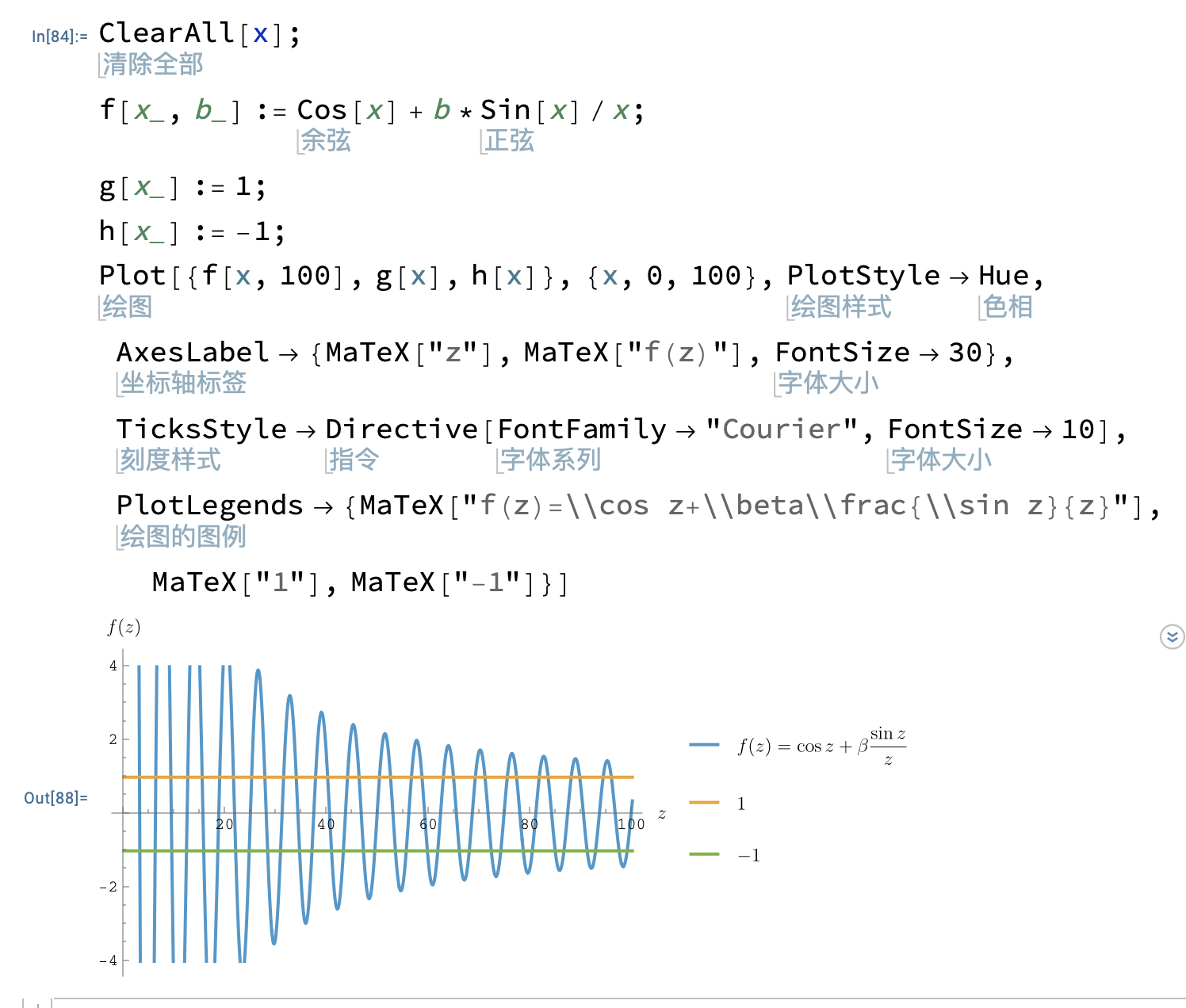
只有在某些区间才存在解，这些区间就是「能带」. 如果能带之间相互导通，那么就是导体；反之为半导体或者绝缘体.

Nondegenerative Perturbation

认为 Hamiltonian 写作 $H=H_0+\lambda H'$ ，这里的 $\lambda H'$ 是微扰的部分，展开各种量：

E_n=E_n^0+\lambda E_n^1+\lambda^2E_n^2+\cdots,\quad \psi_n=\psi_n^0+\lambda\psi_n^1+\lambda^2\psi_n^2+\cdots

方程 $H\psi_n=E_n\psi_n$ 中， $\lambda$ 同幂次的项系数必须相等，比如一阶

H_0\psi_n^1+H'\psi_n^0=E_n^0\psi_n^1+E_n^1\psi_n^0

两边同时作用一个 $\langle\psi_n^0|$ ，则

\braket{\psi_n^0|H_0\psi_n^1}+\braket{\psi_n^0|H'\psi_n^0}=E_n^0\braket{\psi_n^0|\psi_n^1}+E_n^1\braket{\psi_n^0|\psi_n^0}

而 $H_0$ 是一个 Hermite 的算符，可以作用在前后，两者等价，

\braket{\psi_n^0|H_0\psi_n^1}=\braket{H_0\psi_n^0|\psi_n^1}=E_n^0\braket{\psi_n^0|\psi_n^1}

和 RHS 的第一项相消，也就有

E_n^1=\braket{\psi_n^0|H'|\psi_n^0}

所以我们可以完全由零阶的波函数确定微扰产生的能量.

另一个式子是

(E_n^0-H_n^0)\psi_n^1=-(E_n^1-H')\psi_n^0

可以得到

\sum_{m\neq n}(E_n^0-H_n^0)c_{mn}\psi_m^0=(E_n^1-H')\psi_n^0

系数为

c_{mn}=\frac{\braket{\psi_m^0|H'|\psi_n^0}}{E_n^0-E_m^0}

同理，可以计算二阶能量的修正，为

E_n^2=\sum_{m\neq n}\frac{|\braket{\psi_m^0|H'|\psi_n^0}|^2}{E_n^0-E_m^0}

2025/12/3 08:11

查看所有更新日志

版权归属：physnya