菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 4 宇宙中的距离

复制页面

约 2019 字大约 7 分钟

2025-03-10

宇宙的几何

先简单地回顾一下上周讲到的三种膨胀宇宙度规：

ds2=−c2dt2+a2(t)[dx⃗2+k(x⃗⋅dx⃗)21−k∣x⃗∣2]\text{d}s^2=-c^2\text{d}t^2+a^2(t)\left[\text{d}\vec{x}^2+\frac{k(\vec{x}\cdot\text{d}\vec{x})^2}{1-k|\vec{x}|^2}\right]

当然还有球坐标形式：

ds2=−c2dt2+a2(t)[dr21−kr2−r2dΩ2]\text{d}s^2=-c^2\text{d}t^2+a^2(t)\left[\frac{\text{d}r^2}{1-kr^2}-r^2\text{d}\Omega^2\right]

  1. if k=0k=0，平直的 Euclidean 空间；

    ⟶\longrightarrow 零曲率，无限无边.

  2. if k=1k=1，三维的“球面”嵌在四维的 Euclidean 空间中；

    ⟶\longrightarrow 这是一个“有限无边”的宇宙，正曲率.

  3. if k=−1k=-1，三维的“超球面”嵌在四维的 pseudo-Euclidean 空间中.

    ⟶\longrightarrow 负曲率，无限无边.

上面的度规都是某一个 tt 时刻的，但是如果把时间回溯，宇宙总会有一个原初的状态 (虽然 t=0t=0 这个状态在物理上没有定义)：若是正曲率宇宙，宇宙最开始是一个点，是我们直观理解的宇宙大爆炸；但是另外两种模型在无限小的时间 tt 时，实际上仍然是无限大，或者是有限大的，这并不妨碍大爆炸的存在，是一个常见的误区.

19 世纪时，对于哲学家来说，讨论宇宙是否有限是一件重要的事情. 到了现代，我们已经将宇宙是否有限与宇宙的曲率联系在一起了，因此这个哲学问题已经变为一个观测的问题.

这正是科学的魅力：shut up, and calculate! 对于天文，我们当然可以说 shut up, and observe.

-

科学研究就像破案，当你排除掉了所有可能的解释，最后留下的那个解释不管多么反直觉，它都是对的 —— 除非你漏掉了一种更加简单的可能.

如果我们想要构造一个零曲率，但是“有限无边”的宇宙，它的几何结构如何？

一个自然的想法是，在三个维度上都是周期性的边界条件，像是将三个维度均“卷”起来一样.

这时候宇宙就像一个立方体一样，体积能用三重积表示：V=a3L⃗1⋅(L⃗2×L⃗3)V=a^3\vec{L}_1\cdot(\vec{L}_2\times\vec{L}_3).

假如我们看到的 CMB 是有周期性质的，那我们可能能够说我们的宇宙正是这一种模式.

Alas, there is no sign of repetition in CMB or galaxy surveys. 现有的观测证明，暂时不存在这样的周期边界，即使有，其下限也是 ∣L⃗i∣>1010 lyr.|\vec{L}_i|>10^{10}\text{ lyr.}.

-

上面的“Alas”表达的是一种遗憾的语气. 毕竟宇宙学发展了这么多年，似乎越来越无聊了. 当年 LHC 建立时，人们不仅期待它发现 Higgs 粒子，还想要找到一些超出标准模型之外的粒子物理. 但是最大的灾难不在于没找到 Higgs 粒子，而在于只找到了 Higgs 粒子.

宇宙学更甚，现在的研究结果越来越证明，宇宙是平直的，而且越来越发现它很平直. 所以我们现在说，“Alas”.

在下节课上课之前，我们想一个思考题：有没有这样的观测者，使得它观测到的宇宙完全是各向同性的？同时，地球是不是这样的观测者？如何找到这样的参考系呢？

单单从宇宙学原理的角度来讲，不应该有什么差别.

但是地球正在运动，四面八方来的光强度不同，所以我们观测到的 CMB 实际上可能会受到这个效应的影响.

我们之前说过，CMB 的涨落量级是 δTT∼10−4,10−5\frac{\delta T}{T}\sim10^{-4},10^{-5}，而光强的效应强度是 δTT∼(vc)\frac{\delta T}{T}\sim\left(\frac{v}{c}\right).

  • 地球绕日约 30km/s30\text{km/s}，大约 10−410^{-4} 级别的影响；
  • 太阳绕银河系中心约 215km/s215\text{km/s}，10−310^{-3} 级别影响；
  • 银河系绕本星系团 (local group) 中心约 600km/s600\text{km/s}；
  • 本星系团相对“CMB frame”约 627km/s627\text{km/s}.

当然上述几个速度不是同向叠加，所以最终的速度大约是 370km/s370\text{km/s} 左右.

最后一个 CMB frame 实际上是我们反推出来的，因为这个速度影响的量级已经远大于 CMB 涨落了，所以可以分开这两种效应，进而反推出这个完美的观测者的速度.

宇宙中的距离

我们用什么方法测量宇宙中的距离？

三角视差法：测量秒差距，因为已经确定了我们与太阳的距离.

标准烛光：Ia\text{I}a 型超新星的光变周期，能够测量视场中的亮度，和恒定的光变周期进行对比. 典型的天体是造父变星.

标准尺：用一个标准长度作为基准，计算角直径距离.

当然，标准尺方法对应的是一个静止的宇宙，我们测量的是物理距离. 在膨胀宇宙中，我们可能可以看到现在到达我们眼睛的光，但是这时候宇宙已经膨胀了一段时间，所以要乘上尺度因子 —— 但是所有距离均膨胀，所以图形完全相似，最终的张角不变.

angular distance 是

dA=(a(t)a0)a0rd_A=\left(\frac{a(t)}{a_0}\right)a_0r

光度距离 (luminosity distance)：标准烛光测量，我们假定选定的烛光在所有情况下的光度一样，

亮度：

L=ΔEΔtL=\frac{\Delta E}{\Delta t}

流量：

F=ΔEΔtΔA=L4πr2F=\frac{\Delta E}{\Delta t\Delta A}=\frac{L}{4\pi r^2}

所以

dL=L4πF=rd_L=\sqrt{\frac{L}{4\pi F}}=r

这就是静止宇宙下测量的公式.

对于膨胀的宇宙，我们仍然沿用原来的公式的话，会得到

dL=L4πFobsd_L=\sqrt{\frac{L}{4\pi F_{\text{obs}}}}

但是这里我们不知道要不要乘因子. 为简单，考虑单频率光，则我们能够写出流量：

Fobs=ΔEobsΔtobs4π(a0r)2=hνobsΔNobsΔtobsF_\text{obs}=\frac{\Delta E_{\text{obs}}}{\Delta t_\text{obs}4\pi (a_0r)^2}=\frac{h\nu_\text{obs}\Delta N_\text{obs}}{\Delta t_\text{obs}}

但是，

λobs=λem(a0a(t)) ,νobs=νem(a(t)a0)ΔNobs=ΔNem ,Aobs=4π(a0r)2\lambda_\text{obs}=\lambda_\text{em}(\frac{a_0}{a(t)})\,,\quad\nu_\text{obs}=\nu_\text{em}(\frac{a(t)}{a_0})\\\\ \Delta N_\text{obs}=\Delta N_\text{em}\,,\quad A_\text{obs}=4\pi(a_0r)^2

接收面积会变大、光子频率减少，将这些因素考虑到一起，我们应该得到

dL=(a0a(t))a0rd_L=\left(\frac{a_0}{a(t)}\right)a_0r

我们怎么记忆两种方法下的公式呢？

事实上，角距离在光发出的时刻位形就已经确定，于是我们得到的距离就是当时 (光发出时) 的距离，因此为 a(t)ra(t)r.

我们刚刚讲到的都是平直宇宙. 如果现在我们考虑正曲率的一个宇宙呢？

公式肯定是不变的，重要的是 rr 应该是什么：坐标距离 or 投影到 x⃗\vec{x} 的距离. 或者是 ψcom\psi_\text{com} (comoving)，为发光体与观测者在共同时刻的径向距离？

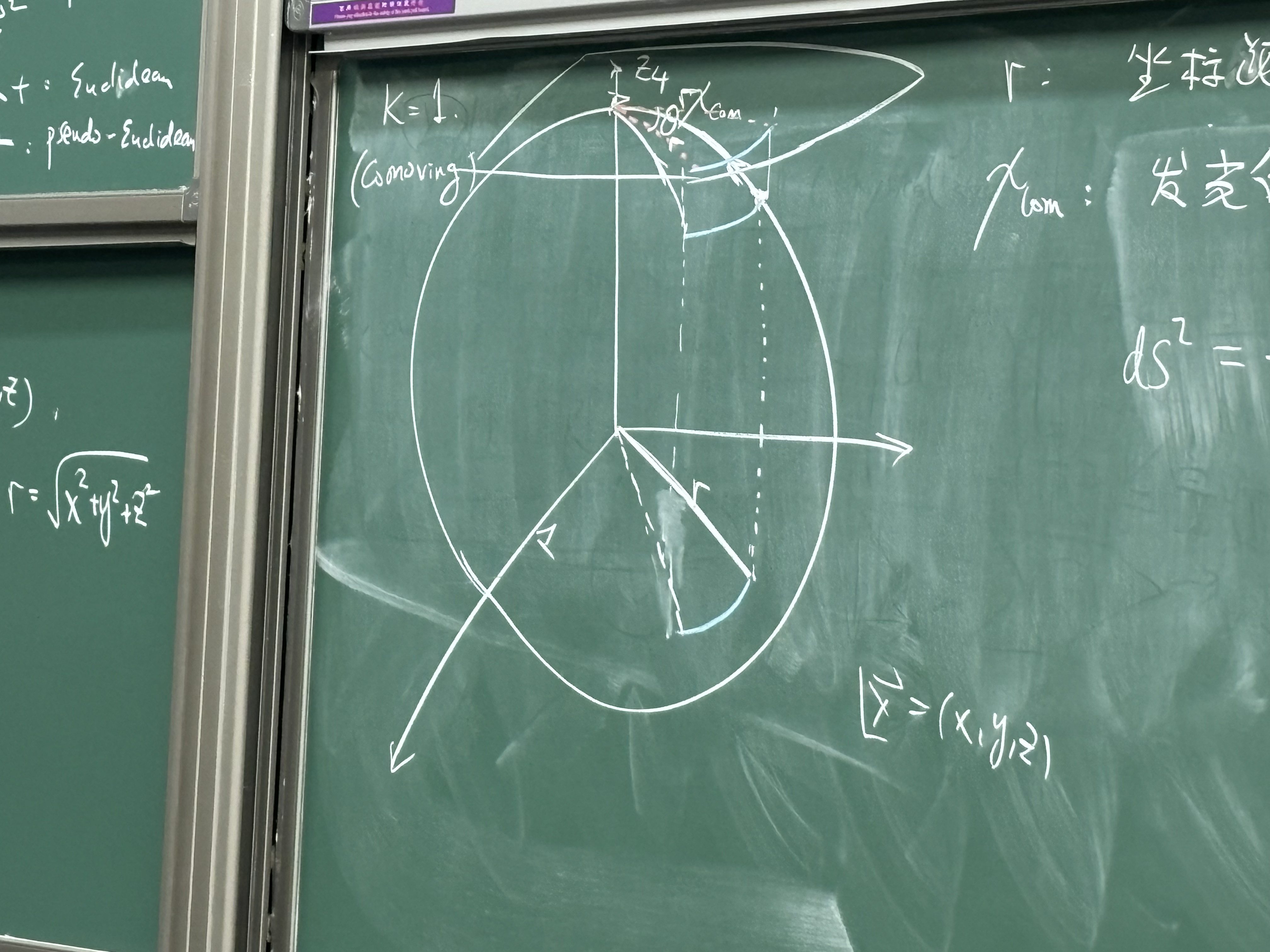
答案其实就是 rr (坐标距离). 原因在于，发出的光在切空间的张角和实际上的张角相同，同时和投影在坐标面上的张角也相同，所以

ds2=−c2dt2+a2(t)[dr21−kr2+r2dθ2+r2sin⁡2θdϕ2]\text{d}s^2=-c^2\text{d}t^2+a^2(t)\left[\frac{\text{d}r^2}{1-kr^2}+r^2\text{d}\theta^2+r^2\sin^2\theta\text{d}\phi^2\right]

在共动时刻，dt=0\text{d}t=0，dr=0\text{d}r=0，dϕ=0\text{d}\phi=0，dθ=Δθ\text{d}\theta=\Delta\theta，所以

dA=lΔθ=a(t)rd_A=\frac{l}{\Delta\theta}=a(t)r

而对于光度距离，图上的这个 ring 实际上是一个二维球面，光沿径向射出，切向的这部分永远不会改变，最后还是在投影空间中计算二维球面的面积，还是 4πr24\pi r^2. 所以最终

ds2=a2(t)r2dΩ2⟹dL=(a(t)a0)a(t)r\text{d}s^2=a^2(t)r^2\text{d}\Omega^2\Longrightarrow d_L=\left(\frac{a(t)}{a_0}\right)a(t)r

更新日志

2026/9/9 05:47
查看所有更新日志
  • d6df0-build(theme): theme update于
  • c3099-build(theme): update theme于
  • f85b5-build(theme): update theme to rc-168于
  • 535f6-fix: some knowledge-based error于
  • 769f2-feat: add cosmos lesson-4 & weekly-18于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)