菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 14 非线性涨落理论

复制页面

约 2726 字大约 9 分钟

2025-5-19

回顾上节课的图像：

在图像以下，重子物质以声学波 (acoustic waves) 的形式传播；同时由于光子与重子的耦合，还有一个 silk damping 效应，来自于光子和重子之间的散射，它抹平了微扰涨落的增长. 总体而言，涨落一般要达到星系团的量级才能呈现增长的态势.

这种结果是不合理的，因此宇宙中不可能只有重子物质，我们现在必须要一种新的物质来支持“现在的涨落尺度”这样的结论.

Dark Matter

暗物质指的是不与重子物质和光发生比较强的相互作用的粒子.

  • 冷暗物质 (Cold Dark Matter, CDM)：自己之间的相互作用也非常微弱，比如 WIMP (Weakly Interacting Massive Particles).

    WIMP 在上世纪 80 年代开始就非常火，因为如果一些理论模型成立，就可以从理论上导出一种物质完美的符合这种特性.

    但是大家利用核反冲等方式来探测 WIMP，这么多年一直都没有得到什么特别的成果，不仅是因为 WIMP 的探测可能会受到各种因素的影响 (比如太阳中微子、超新星爆炸等等)，也有可能是理论上的困难.

  • 热暗物质 (Hot Dark Matter, HDM)：退耦之后的中微子.

    显然这一种观点很早就被排除掉了.

  • 温暗物质 (Warm Dark Matter, WDM)：目前算是一种唯象的模型. 现在的观点差不多是 mDM≳10 keVm_{\text{DM}}\gtrsim10\text{ keV}.

  • 类轴子粒子 (Axion-like Particle)：与 WIMP 相对，这种模型是质量非常小的版本. 但是它们可以通过类似 Bose-Einstein Condensation 的方式，在大尺度上表现得像 WIMP 一样.

    a.k.a fuzzy dark matter, ultra-light particle dark matter, ma∼10−24∼10−1 eVm_a\sim10^{-24}\sim10^{-1}\text{ eV}.

  • 剩下的是一些比较奇怪的模型，比如拓扑缺陷 (Topological defects)：磁单极子、宇宙弦 (Cosmic Strings, 不是弦论中的那种弦，而是宇宙相变过程中遗留的一些缺陷).

    这两种模型的性质我们还算了解得比较多，它们的一些性质确实与暗物质不太一样，所以基本上不太会算进暗物质模型里.

  • 原初黑洞 (Primordial Black Holes)：比较小型的黑洞，产生的效应和我们正常情况下理解的暗物质类似.

我们以冷暗物质为蓝本来研究暗物质的性质.

冷暗物质是“无碰撞”的粒子，原则上来说我们不能使用流体力学的方程. 我们只能写出如下的有效理论：

  1. 连续性方程：

    ∂δ∂t+1a∇⋅[(1+δ)v⃗]=0\frac{\partial\delta}{\partial t}+\frac{1}{a}\nabla\cdot[(1+\delta)\vec{v}]=0

  2. Jeans 方程 (类比 Euler 方程)：

    ∂v⃗∂t+a˙av⃗+1a(v⃗⋅∇)v⃗=−∇Φa−σ2a∇δ1+δ\frac{\partial\vec{v}}{\partial t}+\frac{\dot{a}}{a}\vec{v}+\frac{1}{a}(\vec{v}\cdot\nabla)\vec{v}=-\frac{\nabla\Phi}{a}-\frac{\sigma^2}{a}\frac{\nabla\delta}{1+\delta}

    这里定义速度色散：

    σij≡⟨vivj⟩−⟨vi⟩⟨vj⟩\sigma_{ij}\equiv\braket{v_iv_j}-\braket{v_i}\braket{v_j}

    如果假设各向同性，就得到 σij=σ2δij\sigma_{ij}=\sigma^2\delta_{ij}，再结合均匀性就得到 σ=⟨vi2⟩\sigma=\sqrt{\braket{v_i^2}}.

类似重子流体中做过的分析，可以定义 Jeans 尺度：

λJprop=a(t)λJcom=a(t)⋅2πkJ=σπGρˉ\lambda_J^{\text{prop}}=a(t)\lambda_J^{\text{com}}=a(t)\cdot\frac{2\pi}{k_J}=\sigma\sqrt{\frac{\pi}{G\bar\rho}}

在 λ>λJcom\lambda>\lambda_J^{\text{com}} 时涨落增长. 反之，小于 Jeans 尺度时，无碰撞的暗物质粒子涨落会被抹掉 (free streaming damping).

这样，上面那张图片中可以加入一些新的内容：

一个更加复杂的因素是：因为暗物质和其他物质脱耦的时间在 teqt_{\text{eq}} 之前，所以有一些额外的效果. 在辐射为主的时期，

dδk⃗dt+2a˙adδk⃗dt=4πG(ρˉm+ρˉr)δk⃗\frac{\text{d}\delta_{\vec{k}}}{\text{d}t}+\frac{2\dot{a}}{a}\frac{\text{d}\delta_{\vec{k}}}{\text{d}t}=4\pi G(\bar\rho_m+\bar\rho_r)\delta_{\vec{k}}

可以得到在尺度“大于暗物质决定的 Jeans 长度、小于辐射决定的 Jeans 长度”的这段区域，会出现涨落的停滞.

但是在中微子脱耦之后，暗物质的 Jeans length 比较小，涨落可以增长，暗物质先产生多级结构，暗物质晕开始吸引重子物质，逐渐产生星系.

上面的结构都是线性的 —— δ≪1\delta\ll 1，涨落都是比较小的. 但是实际上涨落增长到一定程度之后，结构已经变得非线性，这时要更换处理方法.

非线性结构

δ≳1\delta\gtrsim1，非线性结构的处理方式有以下几种：

  • 数值模拟：难点在于解读获得的结果，不是很物理.
  • quasi-linear：用高阶的微扰理论，(人 (特指研究生和博士生) 是非常 cheap 的.jpg)，我们得到的结论比较物理.
  • (over-simplified) analytical model：显然不够准确，但是我们会获得一些 insight.

这门课我们主要了解 toy model，如果大家想要了解别的非线性处理方法，可以找鲜于他们.

比较经典的一个 toy model: Spherical Collapse (SC) Model.

在初始时刻，我们研究一个球状的高密度区的膨胀行为，半径 rir_i，over-density is δi\delta_i，宇宙的平均密度是 ρˉi\bar\rho_i.

球体边缘的一个质点 (可以代表整个球边界的演化情况)，受到的引力来自球体 M=M(r<ri)=43πri3ρˉi[1+δi]M=M(r<r_i)=\frac{4}{3}\pi r_i^3\bar\rho_i[1+\delta_i]，随着时间膨胀过程中：

M=43πr3(t)ρˉ(t)[1+δ(t)]M=\frac{4}{3}\pi r^3(t)\bar\rho(t)[1+\delta(t)]

质点所具有的能量的变化：

E=12r˙2−GMr={>0escape=0critical point<0cannot escapeE=\frac{1}{2}\dot{r}^2-\frac{GM}{r}=\left\{\begin{array}{ll} >0&\text{escape}\\ =0&\text{critical point}\\ <0&\text{cannot escape} \end{array}\right.

逃逸情况球体会无限膨胀、无法逃逸的情况球体会先膨胀后收缩.

在 E=0E=0 的临界情况，r(t)∝t2/3r(t)\propto t^{2/3}. 但是宇宙本身也随着 a∝t2/3a\propto t^{2/3} 膨胀 (物质为主的宇宙)，这两个膨胀的速度是同步的，也就是涨落在 comoving 的坐标下，大小是不变的.

如果真的要使得涨落出现有效的增长，我们要求 E<0E<0. 因为如果 E>0E>0，边缘质点会逃逸出去，稀释的速度反而比宇宙膨胀的速度还要快，所以涨落的净增长来自于 E<0E<0 的情况.

现在细致地解决初始能量为负的可能：Ei=Ki+Wi=12vi2−GMri=−KiδiE_i=K_i+W_i=\frac{1}{2}v_i^2-\frac{GM}{r_i}=-K_i\delta_i. 若 δi>0\delta_i>0，则 Ei<0E_i<0，高密度区的 δ(t)\delta(t) 是增长的. 方程的解实际上是一个摆线：

{r=A(1−cos⁡θ)t=B(θ−sin⁡θ) ,0≤θ≤2π\begin{cases} r=A(1-\cos\theta)\\ t=B(\theta-\sin\theta) \end{cases}\,,\quad0\leq\theta\leq2\pi

其中，

A=GM2∣E∣ ,B=GM(2∣E∣)3/2A=\frac{GM}{2|E|}\,,\quad B=\frac{GM}{(2|E|)^{3/2}}

整个高密度球在 t=πBt=\pi B 时达到最高点，之后出现 collapse，塌缩所用时长 tcollapse=2ttat_\text{collapse}=2t_{\text{ta}}，恰好是增长时间的两倍.

在最大半径处：

Eta=−GMrmax⁡=−Hi2ri3(1+δi)2rmax⁡ ,Ei=−Kiδi=−12Hi2ri2δiE_\text{ta}=-\frac{GM}{r_{\max}}=-\frac{H_i^2r_i^3(1+\delta_i)}{2r_{\max}}\,,\quad E_i=-K_i\delta_i=-\frac{1}{2}H_i^2r_i^2\delta_i

两者相等，得到 rmax⁡≈ri/δir_{\max}\approx r_i/\delta_i，只和 over-density 有关系.

同时可以计算 over-density 的变化：

ρ=M43πr3=3M4πA3(1−cos⁡θ)−3ρˉ=16πGt2=16πGB2(θ−sin⁡θ)−21+ε(t)=ρρˉ=92(θ−sin⁡θ)2(1−cos⁡θ)3\begin{aligned} \rho&=\frac{M}{\frac{4}{3}\pi r^3}=\frac{3M}{4\pi A^3}(1-\cos\theta)^{-3}\\ \bar\rho&=\frac{1}{6\pi Gt^2}=\frac{1}{6\pi GB^2}(\theta-\sin\theta)^{-2}\\\\ 1+\varepsilon(t)&=\frac{\rho}{\bar\rho}=\frac{9}{2}\frac{(\theta-\sin\theta)^2}{(1-\cos\theta)^3} \end{aligned}

over-densityturn-aroundcollapse
SC model1+δ(tta)=9π2/161+\delta(t_{\text{ta}})=9\pi^2/16δ(tcollapse)=∞\delta(t_\text{collapse})=\infty
linear modelδ(tta)=3(6π)2/3/20\delta(t_\text{ta})=3(6\pi)^{2/3}/20δ(tcollapse)=3(12π)2/3/20\delta(t_{\text{collapse}})=3(12\pi)^{2/3}/20

其中都用到 tcollapse=2ttat_\text{collapse}=2t_\text{ta}. 对比之下发现线性理论的增长速度明显慢于我们的 toy model (SC). 而且，线性理论的 δ\delta 实际上已经是 ∼1\sim1 量级，不能再适用了.

至此可以得到下面的图像：

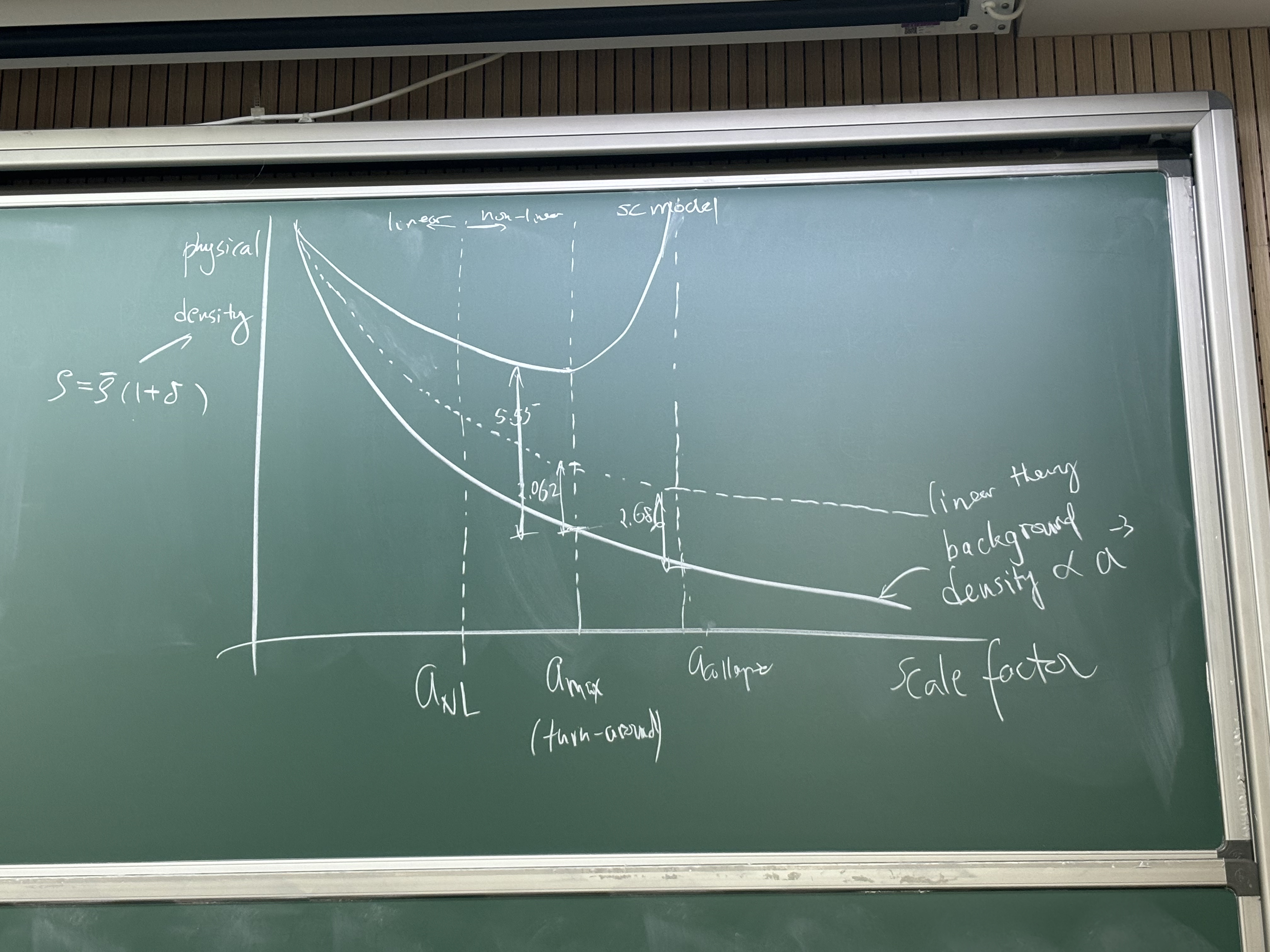
我们这里把线性模型 (外推版) 和宇宙本底的膨胀同时画在一张图像中. 可以发现在膨胀过程中 SC model 的描述比较物理，但是到了收缩阶段，SC model 预言高密度球会收缩成一个奇点，这是非常不合理的. 因此在收缩阶段，我们考察系统达到 virialized (位力化) 的时间：

2Kf+Wf=0 ,Eta=Wta=−GMrtarvir=12rta ,ρvir=8ρta\begin{aligned} 2K_f+W_f&=0\,,\quad E_\text{ta}=W_{\text{ta}}=-\frac{GM}{r_{\text{ta}}}\\ r_{\text{vir}}&=\frac{1}{2}r_{\text{ta}}\,,\quad\rho_{\text{vir}}=8\rho_{\text{ta}} \end{aligned}

得到 virialized 的 over-density：

1+Δvir=1+δ(tcollapse)=ρ(tcollapse)ρˉ(tcollapse)=32(1+δ(tta))=18π21+\Delta_{\text{vir}}=1+\delta(t_\text{collapse})=\frac{\rho(t_{\text{collapse}})}{\bar\rho(t_\text{collapse})}=32(1+\delta(t_\text{ta}))=18\pi^2

修正之后的 SC model 图像，在收缩阶段出现一个振荡，最终形成 bound halo (束缚态的暗物质晕)：

外推的线性模型有什么作用？

我们知道它一定是错的，但是可以当一个“字典”来使用，当我们在 linear theory 中计算出 1.6861.686 的值时，我们就知道 SC model 大概已经进入了 virialized 的阶段. 这里的 1.6861.686 又被称作临界 over-density，表征暗物质晕形成的条件.

同时，当某一区域的暗物质晕密度达到 1+δ≈178(≈18π2)1+\delta\approx178(\approx18\pi^2) 时，我们称之为一个 SC model 的 dark matter halo.

另外，还有一种计算暗物质晕的临界判据是 FoF (friend of friend) 判据，来自暗物质粒子的相互作用范围.

上面我们一直在说球形的初始状态，但是如果初始是椭球，我们可以合理想象这一块暗物质会一开始沿着更短的一条轴塌缩 —— 因为短距离引力更大 (想象一下：星系都是扁平的. 当然，星系是有角动量的，塌缩一个轴之后不会再变化了).

虽然一开始是这么塌缩，最终我们还是会得到一个非常小的球形，形成 halo.

最后简单说一些暗物质晕结构有关的内容：暗物质晕内部的物质分布也不是均匀的，而是符合一种 power law：

ρ(r)=ρ0(rr0)−γ\rho(r)=\rho_0\left(\frac{r}{r_0}\right)^{-\gamma}

在 r0r_0 内部计算体积，会发现若 γ≤3\gamma\leq3，在 r→∞r\to\infty 处 M→∞M\to\infty；反之，在 r→0r\to0 处 M→∞M\to\infty.

提示

如果有什么事情是一个 power law 解决不了的，那么就来两个.

physnya 评：上面这句话简直是至理名言.

double power law 写成：

ρ(r)=ρ0(r/rs)γ[1+(r/rs)α](β−γ)/α={∝r−γr≪rs∝r−βr≫rs\rho(r)=\frac{\rho_0}{(r/r_s)^\gamma[1+(r/r_s)^\alpha]^{(\beta-\gamma)/\alpha}}=\left\{\begin{array}{ll} \propto r^{-\gamma}&r\ll r_s\\ \propto r^{-\beta}&r\gg r_s \end{array}\right.

这是所谓的 NFW profile.

目前没有解决的问题是：暗物质晕中心的部分并不是按照这样的规律变化，而是有一个平缓的区域，这对冷暗物质模型是一个挑战.

更新日志

2025/10/9 02:50
查看所有更新日志
  • f85b5-build(theme): update theme to rc-168于
  • c5098-fix(display): KaTeX于
  • 94854-feat(note): add cosmos note于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)