菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 13 线性微扰理论

复制页面

约 3061 字大约 10 分钟

2025-5-10

从这节课开始讲星系，理论推导会变得稍微少一点.

如果对于星系比较感兴趣，可以学习几门研究生课程，比如 CGM (星际介质)、星系动力学等等.

线性微扰理论

大爆炸后 38 万年，宇宙产生原初涨落.

物理上的方程，在一阶的近似下都是线性的，所以我们一开始要来讲线性的微扰理论. 对于宇宙的物质结构，显然在今天我们能够把大尺度范围的宇宙物质分布看成一个连续场. 现在我们把宇宙物质分布处理为一个连续的流体：

提示

夏天，北极熊站在海边，等着三文鱼从水中跳出来，就可以很容易地抓到鱼；这时，北极熊是一个 observer，它关注的是“三文鱼”流体的密度 ρ(r⃗,t)\rho(\vec{r},t)、速度 u⃗(r⃗,t)\vec{u}(\vec{r},t)、压强 P(r⃗,t)P(\vec{r},t) (决定了鱼出来的“强度”).

这里，r⃗\vec{r} 是物理坐标，tt 是时间.

描述流体的方程有以下几个：

  • 连续性方程：

    DρDt+ρ∇r⃗⋅u⃗=0\frac{\text{D}\rho}{\text{D}t}+\rho\nabla_{\vec{r}}\cdot\vec{u}=0

    这里，D\text{D} 是 Lagrangian derivative，指的是

    DDt:=∂∂t∣r⃗Eulerian derivative+u⃗⋅∇r⃗due to the streaming\frac{\text{D}}{\text{D}t}:=\underset{\text{Eulerian derivative}}{\left.\frac{\partial}{\partial t}\right|_{\vec{r}}}+\underset{\text{due to the streaming}}{\vec{u}\cdot\nabla_{\vec{r}}}

  • Euler 方程：

    Du⃗Dt=−∇r⃗Pρ−∇r⃗ ϕ\frac{\text{D}\vec{u}}{\text{D}t}=-\frac{\nabla_{\vec{r}}P}{\rho}-\nabla_{\vec{r}}\,\phi

    其中 ϕ=ϕ(r⃗,t)\phi=\phi(\vec{r},t) 为势能.

  • Poisson 方程：

    ∇r⃗2 ϕ=4πGρ\nabla^2_{\vec{r}}\,\phi=4\pi G\rho

    (这个方程仅仅对引力势成立，来源于 Newton 的引力公式)

  • 到这里为止我们还差一个方程，因此对于特定的流体，还要引入物态方程：P=P(ρ)P=P(\rho).

在一个膨胀的宇宙中，某点物理坐标 r⃗\vec{r} 不是一个常数，所以我们在研究这类问题时必须换成共动坐标 x⃗\vec{x}. 已经知道，r⃗=a(t)x⃗\vec{r}=a(t)\vec{x}，对于 u⃗\vec{u}，应该改写成：

u⃗=a˙(t)x⃗Hubble flow+v⃗\vec{u}=\underset{\text{Hubble flow}}{\dot{a}(t)\vec{x}}+\vec{v}

其他的改写：

∇r⃗=1a(t)∇x⃗∂∂t∣r⃗=∂∂t∣x⃗−a˙ax⃗⋅∇x⃗\begin{aligned} \nabla_{\vec{r}}&=\frac{1}{a(t)}\nabla_{\vec{x}}\\\\ \left.\frac{\partial}{\partial t}\right|_{\vec{r}}&=\left.\frac{\partial}{\partial t}\right|_{\vec{x}}-\frac{\dot{a}}{a}\vec{x}\cdot\nabla_{\vec{x}} \end{aligned}

以下省略下标 x⃗\vec{x}.

引入线性微扰：ρ(x⃗,t)=ρ(t)[1+δ(x⃗,t)]\rho(\vec{x},t)=\rho(t)[1+\delta(\vec{x},t)]，上面的流体力学方程改写为：

  • 连续性方程：

    ∂δ∂t+1a∇⋅(1+δ)v⃗=0\frac{\partial\delta}{\partial t}+\frac{1}{a}\nabla\cdot(1+\delta)\vec{v}=0

  • Euler 方程：

    ∂v⃗∂t+a˙av⃗+1a(v⃗⋅∇)v⃗=−∇Paρˉ(1+δ)−∇Φa\frac{\partial\vec{v}}{\partial t}+\frac{\dot{a}}{a}\vec{v}+\frac{1}{a}(\vec{v}\cdot\nabla)\vec{v}=-\frac{\nabla P}{a\bar\rho(1+\delta)}-\frac{\nabla\Phi}{a}

  • Poisson 方程：

    ∇2Φ=4πGρˉa2δ\nabla^2\Phi=4\pi G\bar\rho a^2\delta

修正的引力势是：

Φ(x⃗,t)=ϕ+12aa¨∣x⃗∣2\Phi(\vec{x},t)=\phi+\frac{1}{2}a\ddot{a}|\vec{x}|^2

提示

值得注意的是，v⃗=a(t)x⃗˙\vec{v}=a(t)\dot{\vec{x}} 不是共动坐标中的速度，而是一个物理上的速度.

对于理想气体，有物态方程：

P=nkBT=ρμmpkBTP=nk_BT=\frac{\rho}{\mu m_p}k_BT

(μ\mu 是平均分子量)

比内能：

ϵ=1γ−1kBTμmp\epsilon = \frac{1}{\gamma-1}\frac{k_BT}{\mu m_p}

若是单原子分子气体，γ=5/3\gamma=5/3，于是比内能是 ϵ=3P/2ρ\epsilon=3P/2\rho，代入热力学基本方程：

d(Pρ)=23dϵ=23[TdS−Pd(1ρ)]⟹dPρ=2μmp3kBdS+53dln⁡ρ⟹P(ρ,S)∝ρ5/3exp⁡(2μmp3kBS)⟹∇Pρˉ=1ρˉ[(∂P∂ρ)S∇ρ+(∂P∂S)ρ∇S]=cS2∇δ+23T(1+δ)∇S\begin{aligned} \text{d}\left(\frac{P}{\rho}\right)&=\frac{2}{3}\text{d}\epsilon=\frac{2}{3}\left[T\text{d}S-P\text{d}\left(\frac{1}{\rho}\right)\right]\\\\ \Longrightarrow\frac{\text{d}P}{\rho}&=\frac{2\mu m_p}{3k_B}\text{d}S+\frac{5}{3}\text{d}\ln\rho\\\\ \Longrightarrow P(\rho,S)&\propto\rho^{5/3}\exp\left(\frac{2\mu m_p}{3k_B}S\right)\\\\ \Longrightarrow\frac{\nabla P}{\bar\rho}&=\frac{1}{\bar\rho}\left[\left(\frac{\partial P}{\partial\rho}\right)_S\nabla\rho+\left(\frac{\partial P}{\partial S}\right)_\rho\nabla S\right]\\\\ &=c_S^2\nabla\delta+\frac{2}{3}T(1+\delta)\nabla S \end{aligned}

其中 cSc_S 是声速. 这样就把 Euler 方程的 RHS\text{RHS} 更换为上面的一个量. 到目前为止，未知量有 δ(x⃗,t)\delta(\vec{x},t)，v⃗(x⃗,t)\vec{v}(\vec{x},t) (本动速度)，Φ(x⃗,t)\Phi(\vec{x},t) 和 S(x⃗,t)S(\vec{x},t) 五个，方程则有：连续性方程、Euler 方程的三个分量方程和 Poisson 方程，恰好可以解出答案.

现在，为了解决这几个方程，我们需要进行线性化：思路是，涨落 δ≪1\delta\ll 1. 而本动速度 v⃗=a(t)x⃗˙\vec{v}=a(t)\dot{\vec{x}} 完全是由涨落引起的，因此也是一个小量；同理，∇S\nabla S 和 Φ(∝δ)\Phi(\propto\delta) 也是小量. 原来的三个方程改为：

∂δ∂t+1a∇⋅v⃗=0∂v⃗∂t+a˙av⃗+1a(v⃗⋅∇)v⃗=−∇Φa−cS2∇δa(1+δ)−2Tˉ3a(1+δ)∇S∇2Φ=4πGρˉa2δ\begin{aligned} &\frac{\partial\delta}{\partial t}+\frac{1}{a}\nabla\cdot\vec{v}=0\\\\ &\frac{\partial\vec{v}}{\partial t}+\frac{\dot{a}}{a}\vec{v}+\cancel{\frac{1}{a}(\vec{v}\cdot\nabla)\vec{v}}=-\frac{\nabla\Phi}{a}-\frac{c_S^2\nabla\delta}{a(1+\cancel{\delta})}-\frac{2\bar{T}}{3a}(1+\cancel{\delta})\nabla S\\\\ &\nabla^2\Phi=4\pi G\bar\rho a^2\delta \end{aligned}

联立，有：

∂2δ∂t2+2a˙a∂δ∂t‾Hubble drag=4πGρˉδ‾gravity+cS2a2∇2δ‾pressure+2Tˉ3a2∇2S‾entropy\frac{\partial^2\delta}{\partial t^2}+\underset{\text{Hubble drag}}{\underline{2\frac{\dot{a}}{a}\frac{\partial\delta}{\partial t}}}=\underset{\text{gravity}}{\underline{4\pi G\bar\rho\delta}}+\underset{\text{pressure}}{\underline{\frac{c_S^2}{a^2}\nabla^2\delta}}+\underset{\text{entropy}}{\underline{\frac{2\bar{T}}{3a^2}\nabla^2S}}

将宇宙中的密度分为物质密度和辐射密度，那么 δ⋅ρˉ=ρˉrδr+ρˉmδm\delta\cdot\bar\rho=\bar\rho_r\delta_r+\bar\rho_m\delta_m，在这样的观点下，宇宙的涨落分为两种模式：

  • iso-curvature perturbation (总体涨落为零，两种涨落抵消)，那么有关系：

    δrδm=−ρˉmρˉr=−aaeq\frac{\delta_r}{\delta_m}=-\frac{\bar\rho_m}{\bar\rho_r}=-\frac{a}{a_{\text{eq}}}

    其中 aeqa_{\text{eq}} 是辐射和物质相等的时刻的尺度因子. 特别地，在辐射为主导的时代，ρˉr≫ρˉm\bar\rho_r\gg\bar\rho_m，δr≈0\delta_r\approx0.

  • entropy perturbation：考虑熵的涨落，

    δS=S(x⃗,t)−Sˉ(t)Sˉ(t)S=sV∝Sρm∝T3ρm∝ρr3/4ρmδS=δSS=1S[∂S∂ρrδρr+∂S∂ρmδρm]=34δr−δm\begin{aligned} \delta_S&=\frac{S(\vec{x},t)-\bar{S}(t)}{\bar{S}(t)}\\ S&=sV\propto\frac{S}{\rho_m}\propto\frac{T^3}{\rho_m}\propto\frac{\rho_r^{3/4}}{\rho_m}\\\\ \delta_S&=\frac{\delta S}{S}=\frac{1}{S}\left[\frac{\partial S}{\partial\rho_r}\delta\rho_r+\frac{\partial S}{\partial \rho_m}\delta\rho_m\right]=\frac{3}{4}\delta_r-\delta_m \end{aligned}

    这种模式又称 adiabatic perturbation / iso-entropic perturbation.

之后我们一般讨论后一种模式，因为实验上这种模式符合得更好.

为了解上面的方程，作 Fourier 变换 (∇→ik⃗\nabla\to\text{i}\vec{k}，∇2→−k2\nabla^2\to-k^2，δ(x⃗)→δk⃗\delta(\vec{x})\to\delta_{\vec{k}})：

d2δk⃗dt2+2a˙adδk⃗dt=[4πGρˉ−cS2k2a2]δk⃗−2Tˉ3a2k2Sk⃗\frac{\text{d}^2\delta_{\vec{k}}}{\text{d}t^2}+2\frac{\dot{a}}{a}\frac{\text{d}\delta_{\vec{k}}}{\text{d}t}=\left[4\pi G\bar\rho-\frac{c_S^2k^2}{a^2}\right]\delta_{\vec{k}}-\frac{2\bar{T}}{3a^2}k^2S_{\vec{k}}

提示

注意到：这里把偏微分写成了全微分，这并不是真的 δk⃗\delta_{\vec{k}} 和 k⃗\vec{k} 没关系了，而是代表每一个固定的 k⃗\vec{k} 不依赖于其他的模，单独演化，所以可以认为在每一个单独的 k⃗\vec{k}，δk⃗\delta_{\vec{k}} 都是只与 tt 有关的.

(1) adiabatic perturbation，且绝热演化 (没有熵的输入)：Sk⃗=0S_{\vec{k}}=0. 且我们暂时忽略宇宙膨胀带来的影响，所以 Hubble drag 一项也是零. 这时整个方程变成了我们特别了解的一个微分方程：

d2δk⃗dt2+ω2δk⃗=0 ,ω2:=k2cS2a2−4πGρˉ\frac{\text{d}^2\delta_{\vec{k}}}{\text{d}t^2}+\omega^2\delta_{\vec{k}}=0\,,\quad\omega^2:=\frac{k^2c_S^2}{a^2}-4\pi G\bar\rho

  1. ω2>0\omega^2>0，δk⃗∝e±iωt\delta_{\vec{k}}\propto e^{\pm\text{i}\omega t} 振荡解，涨落大小没有增长；
  2. ω2<0\omega^2<0，δk⃗∝e∓αt\delta_{\vec{k}}\propto e^{\mp\alpha t} (ω=iα\omega=\text{i}\alpha)，取 "−-" 时衰减解忽略，取 "++" 时为增长解 (growing mode).

引入 Jeans mode (注意是共动坐标下的波数)：

kJ:=2acSπGρˉ ,ω2=cS2a2(k2−kJ2)k_J:=\frac{2a}{c_S}\sqrt{\pi G\bar\rho}\,,\quad\omega^2=\frac{c_S^2}{a^2}(k^2-k_J^2)

所以振荡解就要求 k>kJk>k_J，λ<λJ\lambda<\lambda_J (共动坐标下的 Jeans 长度，λJ=2π/kJ\lambda_J=2\pi/k_J). 也就是当涨落尺度小于 Jeans 长度，涨落就不能增长；反之，若涨落尺度大于 Jeans 长度，涨落就能够按照指数模式增长.

上面是在共动坐标下面讨论，我们当然还可以定义一个物理坐标下的 Jeans 长度，定义为：

λJproper=a(t)λJcom=cSπGρˉ\lambda_J^{\text{proper}}=a(t)\lambda_J^{\text{com}}=c_S\sqrt{\frac{\pi}{G\bar\rho}}

定义这一个物理坐标的 Jeans 长度，是因为我们有时想要用质量来描述一个空间尺度，这时候要引入 Jeans 质量，而这个 Jeans 质量对应的应该是物理的 Jeans 长度，也就是

MJ=43π(λJproper2)3⋅ρˉ=π6(λJproper)3M_J=\frac{4}{3}\pi\left(\frac{\lambda_J^{\text{proper}}}{2}\right)^3\cdot\bar\rho=\frac{\pi}{6}(\lambda_J^{\text{proper}})^3

上述 Jeans 波数、Jeans 波长和 Jeans 质量等等一系列判据统称为 Jeans 判据，在很多宇宙学的分支都能见到，因为其本质就是波动方程带来的效果：大尺度的涨落可以增长，小尺度的涨落不能增长.

(2) Hubble drag：考虑宇宙膨胀的影响 (但是仍然是 adiabatic perturbation，Sk⃗=0S_{\vec{k}}=0)，并假设 k≪kJk\ll k_J.

方程变为：

d2δk⃗dt2+2a˙adδk⃗dt=4πGρˉδk⃗\frac{\text{d}^2\delta_{\vec{k}}}{\text{d}t^2}+2\frac{\dot{a}}{a}\frac{\text{d}\delta_{\vec{k}}}{\text{d}t}=4\pi G\bar\rho\delta_{\vec{k}}

这时我们可以解出这样的解：

δ+∝H(t)∫0tdt′a2(t′)H2(t′)\delta_+\propto H(t)\int_0^t\frac{\text{d}t'}{a^2(t')H^2(t')}

若假设这里是物质为主的宇宙，则还可以进一步得到

∝H(z)∫z∞1+z′E3(z′)dz′∝t2/3\propto H(z)\int_z^\infty\frac{1+z'}{E^3(z')}\text{d}z'\propto t^{2/3}

可以发现，增长的规律从指数变为幂律，Hubble 常数 (宇宙的膨胀) “拖慢”了增长的速度，所以称为 Hubble drag.

(3) “视界”因素：计入 Poisson 方程的影响，

−k2Φk⃗=4πGa2ρˉδk⃗-k^2\Phi_{\vec{k}}=4\pi Ga^2\bar\rho\delta_{\vec{k}}

有些涨落的尺度非常巨大，超过了视界的范围 (λ>λH\lambda>\lambda_H)，称为 super-horizon perturbation，在视界以外，势能的涨落传播不过来，所以 Φk⃗=const.\Phi_{\vec{k}}=\text{const.}，因此这里有

δk⃗∝(ρˉa2)−1∝{amattera2radiation\delta_{\vec{k}}\propto(\bar\rho a^2)^{-1}\propto\left\{\begin{array}{ll} a&\text{matter}\\ a^2&\text{radiation} \end{array}\right.

涨落可以增长；相对地，在视界内部的涨落 (sub-horizon perturbation，λ<λH\lambda<\lambda_H) 就难以增长.

下面我们汇总不同尺度的涨落：

(1) 在 recombination 之前，首先考虑 teqt_{\text{eq}} 前的时刻，baryon 和 radiation 还没有解耦，这时宇宙以辐射为主，ρˉb(t)\bar\rho_b(t) (baryon 密度) ≪ρˉr(t)\ll\bar\rho_r(t)，

cS=(∂P∂ρ)S=c3[1+3ρˉb(t)4ρˉr(t)]−1/2≈c3c_S=\sqrt{\left(\frac{\partial P}{\partial\rho}\right)_S}=\frac{c}{\sqrt3}\left[1+\frac{3\bar\rho_b(t)}{4\bar\rho_r(t)}\right]^{-1/2}\approx\frac{c}{\sqrt3}

(2) 在 teq<t<trect_{\text{eq}}<t<t_{\text{rec}} 时，宇宙以物质为主，这时 ρˉb≫ρˉr\bar\rho_b\gg\bar\rho_r，

cS∝(ρˉbρˉr)−1/2∝a−1/2c_S\propto\left(\frac{\bar\rho_b}{\bar\rho_r}\right)^{-1/2}\propto a^{-1/2}

这时 Jeans 质量大约是 MJ≈1.2×1016(Ωbh2)M∘M_J\approx1.2\times10^{16}(\Omega_bh^2)M_{\circ}，这是一个超星系团的质量.

(3) t>trect>t_{\text{rec}}，声速公式发生变化，再复合结束之后，仍然是物质为主，

cS=(∂P∂ρ)S=γPρ=(5kBT3μmp)1/2∝T1/2∝a−1c_S=\sqrt{\left(\frac{\partial P}{\partial\rho}\right)_S}=\sqrt{\frac{\gamma P}{\rho}}=\left(\frac{5k_BT}{3\mu m_p}\right)^{1/2}\propto T^{1/2}\propto a^{-1}

这是因为光子和重子脱耦之后，重子场的压强主要来源于重子场自身，而不是之前的光子场，声速突变.

在这个时期，Jeans 质量约是 1.5×105(Ωbh2)M∘1.5\times10^{5}(\Omega_bh^2)M_\circ，这是球状星系团的特征质量.

实际上，除了上述因素，还有一种 silk damping 效应会影响涨落的效果. 这来源于 t<trect<t_{\text{rec}} 时期的光子与重子散射过程，这会把光子自由程之内的涨落直接“抹平”. 光子自由程是 σ∝(σTne)−1\sigma\propto(\sigma_Tn_e)^{-1}，散射次数 N=ct/λN=ct/\lambda. 光子随机游走，产生了这种效应的特征尺度：

λd=(N3)1/2λ=(ct3σTne)1/2\lambda_d=\left(\frac{N}{3}\right)^{1/2}\lambda=\left(\frac{ct}{3\sigma_Tn_e}\right)^{1/2}

这是 damping scale.

如果再考虑 super-horizon perturbation，这个涨落模式是否可以增长由 Hubble length 来判别，和 Jeans length、damping scale 画在一起，得到如下图像：

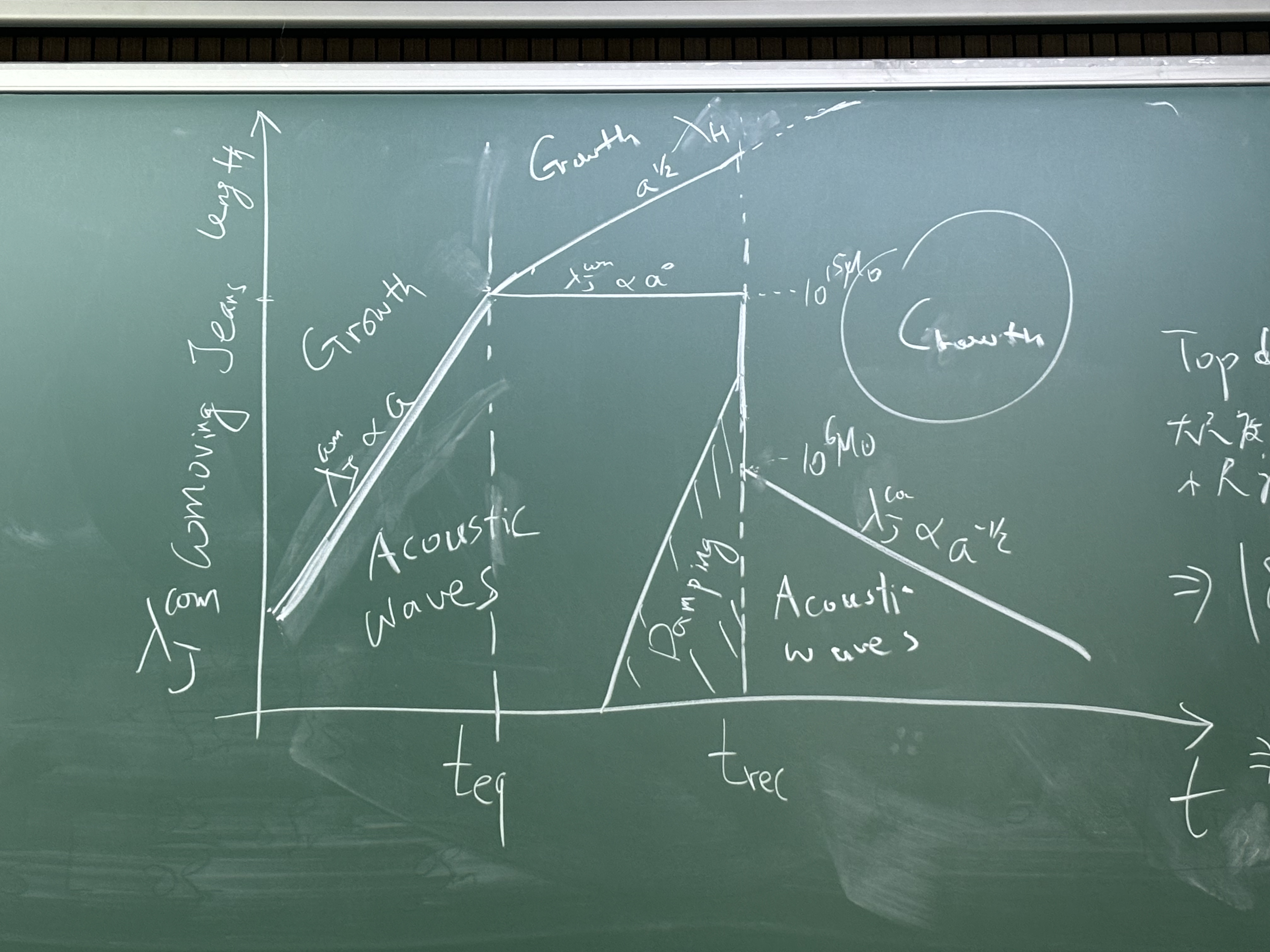
这些曲线的上方尺度的涨落才可以增长，于是较小尺度的涨落直到 trec=38t_{\text{rec}}=38 万年之后、λJ\lambda_J 开始衰减时才能增长. 这造成的结果是所谓 top down scenario，也就是大尺度的涨落先增长，小的涨落后增长.

但是，这些理论要求在 trect_{\text{rec}} 时，相对涨落达到 10−310^{-3} 量级，到目前的宇宙年龄，才可能出现星系结构 —— 但是实际上 CMB 的观测结果，那时的涨落只有 10−510^{-5} 量级.

something must be wrong!

这也就引出 top down scenario 的修正，存在一种与重子物质声学性质不同的物质 (暗物质)，它自己很早就脱耦了，大大压低了 Jeans 长度，为星系的形成提供了一个温床.

更新日志

2025/10/9 02:50
查看所有更新日志
  • f85b5-build(theme): update theme to rc-168于
  • f7ea5-feat(note): add cosmos note于
  • 6749c-feat(note): add cosmos note于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)