注意

上一次课程因为与实验课冲突，我没有参加，需要根据其他同学的笔记进行整理，可能会晚不少时间上传.

下一次课是这周六的晚上，还是在原来那个教室.

上节课讲的是中微子的退耦过程，最后留了一个伏笔是中微子温度与宇宙微波背景辐射的温度有一定差异. 再讲完今天这节课，我们宇宙学的部分就基本结束了.

极早期宇宙的历史

这节课要讲的是 neutrino decoupling 和 inflation.

我们把 $1\text{ MeV}$ 视为中微子退耦的温度，在这之前，$(e,\nu,\gamma)$ 是热平衡的，过了这个温度中微子将会和 $(e,\gamma)$ 这个体系退耦，但是因为没有外界的能量输入，所以温度只是随着尺度因子 $a$ 的变化而缓慢改变.

电子和光子可以通过 Compton 散射等过程达到热平衡，因此更难以退耦.

之后的分界点是 $0.5\text{ MeV}$，在这个点之前，$e$ 是相对论性的，之后速度下降变为非相对论性，在这个过程中电子和光子一直都是热平衡的，不过反应 $e^++e^-\longleftrightarrow\gamma+\gamma$ 的能量变低，平衡大幅向右移动，正负电子对大量湮灭，这使得光子体系的能量升高 ($T_\gamma$ 升高)，与之平衡的电子气温度也升高 (当然，升高之后还是以 $1/a$ 的模式降温).

上节课我们从热力学角度推导了几个统计量 (对于相对论性粒子，非相对论性粒子的贡献在低阶近似下可以忽略)：

$$\rho(T)=\mathcal{N}\cdot\frac{1}{2}a_BT^4\,,\quad S(T)=\mathcal{N}\cdot\frac{2}{3}a_BT^3\,,\quad P(T)=\frac{1}{3}\rho(T)$$

其中，$\mathcal{N}$ 是所谓的“简并度”，对于不同的 particle types，有不同的值，上节课有讲到过.

熵密度 $S(T)$ 守恒，也就是 $\mathcal{N}T^3a^3=\text{const}$. (对于一个与外界没有热量交换的系统)

P.S. 数密度 $n(T)$ 不能简单地用 $\mathcal{N}$ 来计算.

(1) 对于电子 - 光子体系，在中微子退耦时刻，$T_\nu=T_\gamma=T_{\text{dec}}$.

(2) 在之后的一个时刻，$t_*\gg t_{\text{dec}}$，同时温度 $T(t_*)\ll0.5\text{ MeV}$，这时有一个守恒的方程：

$$\mathcal{N}(t_{\text{dec}})T_{\text{dec}}^3a^3(t_{\text{dec}})=\mathcal{N}(t_*)T^3_\gamma(t_*)a^3(t_*)$$

具体计算简并度：

$$\begin{aligned} \mathcal{N}(t_{\text{dec}})&=2+1\times2\times2\times\frac{7}{8}=\frac{11}{2}\\ \mathcal{N}(t_*)&=2 \end{aligned}$$

(3) After $t>t_\text{dec}$，$T_\nu\propto1/a$，对于中微子，

$$T_\text{dec}a(t_{\text{dec}})=T_\nu(t_*)a(t_*)$$

代入上面的守恒方程，得到

$$\frac{T_\nu(t_*)}{T_\gamma(t_*)}=\left[\frac{\mathcal{N}(t_*)}{\mathcal{N}(t_{\text{dec}})}\right]^{1/3}=\left(\frac{4}{11}\right)^{1/3}\approx\frac{1}{1.4}$$

(4) After $t>t_*$，$T_\gamma\propto1/a$，$T_\nu\propto1/a$，一直到今天.

因此，中微子的微波背景辐射 C$\nu$B 温度 (虽然非常难测量) 大约是 CMB 的 $1/1.4$，原因就在于 $0.5\text{ MeV}$ 时正负电子大量湮灭注入的能量只给了光子，但是早前中微子已经脱耦，没有得到这一部分能量.

宇宙辐射能量密度：

$$\begin{aligned} \rho_{R,0}&=\rho_{\gamma,0}+\rho_{\nu,0}\\\\ &=\frac{1}{2}a_BT^4\left[ \underset{\gamma}{\underline{2}}+\underset{3\text{ flavours}}{\underline{3}}\times\underset{\nu^+\,\&\,\nu^-}{\underline{2}}\times\underset{\nu\,\&\,\bar\nu}{\underline{2}}\times\underset{\text{spin - }1}{\underline{1}}\times\frac{7}{8}\times\underset{(T_{\nu,0}/T_{\gamma,0})^4}{\underline{\left(\frac{4}{11}\right)^{4/3}}} \right]\\\\ &\approx1.681\rho_{\gamma,0} \end{aligned}$$

其中后面一长串就是中微子的贡献.

Inflation

我们刚刚说到中微子脱耦的时间大约是温度 $1\text{ MeV}$ 的量级，但是暴涨时期的能标就远远高于这个量级，虽然我们还不能确定具体的数量级，但是可以知道的是，这个能量已经达到了 $10^{13}\sim10^{15}\text{ GeV}$ 的级别.

事实上暴涨理论并不是建立在一个已知的粒子物理基础上的，而是为解决某些大爆炸理论的疑难而提出的一个修正，因此我们先要来介绍疑难在哪里：

(1) Flatness Problem (平坦性问题)：严格来讲这并不是大爆炸理论的致命问题，或许我们不应该叫它疑难，而是应该叫它问题.

我们先来考虑物质为主导的宇宙 (因为那时暗能量的作用还完全不明显，辐射甚至没有脱耦)，考虑一个以物质为主导的宇宙的平坦性：

$$\begin{aligned} \Omega(t)&=\frac{\rho_m(t)}{\rho_{c}(t)}=\frac{\Omega_m\left(\frac{3H_0^2}{8\pi G}\right)\left(\frac{a}{a_0}\right)^3}{\frac{3H^2(t)}{8\pi G}}\\ &=\frac{\Omega_m(a/a_0)^{-3}}{\Omega_m(a/a_0)^{-3}+\Omega_K(a/a_0)^{-2}}\\\\ &=\left[1+\frac{\Omega_K}{\Omega_m}\left(\frac{a}{a_0}\right)\right]^{-1} \end{aligned}$$

其中用到：

$$\frac{H^2}{H_0^2}=E^2(t)=\Omega_m\left(\frac{a}{a_0}\right)^{-3}+\Omega_K\left(\frac{a}{a_0}\right)^{-2}$$

则：

$$|\Omega(t)-1|=\left|1+\frac{\Omega_m}{\Omega_K}\frac{a_0}{a}\right|^{-1}\underset{\sim}{\propto} a$$

假设 $\Omega_m=0.9$，$\Omega_K=0.1$，我们发现，红移越大，上面的量急剧趋于 $0$，这意味着宇宙的初始条件是极度平坦的 -- 这似乎并不显然.

提示

这一问题和后面第四个问题类型一样，你当然可以说宇宙的初条件就是这样的，这并没有违反任何的理论. —— 但是我们就是想要弄清楚为什么.

(2) Horizon Problem (视界疑难)：这下就是疑难了，这个问题相较于平坦性问题要严重许多.

CMB 是高度均匀的. 但是均匀就意味着热平衡，那么在 CMB 形成的时间内，宇宙中我们现在能够看到的最远两点必须发生一些相互作用.

$$d_H(t_{\text{rec}})\approx\frac{H_0^{-1}}{\Omega_m^{1/2}(1+z_{\text{rec}})^{3/2}}\approx1\degree/\text{whole sky}$$

也就是说，in principle, $T_{\text{CMB}}$ is isotropic only within $1\degree$. 大爆炸理论的预言应该要求 CMB 极度各向异性！

提示

早期人们的观点是相反的，因为他们在计算上犯了一些错误，但是正因如此，当两位工程师发现极为各向同性的微波背景辐射时，他们认为这是大爆炸理论的例证. 或许历史总是在螺旋上升的.

(3) Magnetic Monopole Problem (磁单极子问题)：这件事在上世纪七八十年代是个严重的疑难，当然现在早已解决.

当时的物理学界陷入了追求大一统理论的狂潮之中，粒子标准模型来源于弱电统一理论 (写成群乘法是 $SU(2)\otimes U(1)$)，后来强相互作用并入这个理论，是以一种“正交”的方式加入进来的，而不是像弱电统一一样将几种力混合在一起.

人们想要将引力理论也并入上述框架，提出了所谓的 GUT (Great Uniform Theory). 这个理论统一由 $SU(5)$ 群进行刻画，但是这个群的对角元预言了单极子的存在.

那时的物理学家想不出这个 GUT 有什么问题，但是又找不到磁单极子，这意味着磁单极子在宇宙中的密度低得超乎想象.

GUT 的能标在 $10^{15}\text{ GeV}$ 左右，能量降低时的对称性自发破缺产生磁单极子. 若假设“相变”在一个视界体积内产生 1 个磁单极子，则：

$$\frac{n_\text{MP}}{n_\gamma}\sim10^{-4}\,,\quad m_{\text{MP}}\sim T_{\text{GUT}}$$

(质量比核子高 $15$ 个数量级，密度也比核子高了 $1$ 个数量级) 我们可以依照这两个条件来计算 $\Omega_{\text{MP}}$，发现 $\Omega_{\text{MP}}\sim10^{19}\gg1$，荒谬至极.

提示

不过到现在，这已经不太算是一个疑难了，因为只有那时的物理学家如同宗教一般信仰着 GUT，他们总觉得是 something missing，才提出了暴涨. 实际上这也是推动暴涨理论诞生最重要的一个问题.

$SU(5)$ 在后面预言的质子衰变被实验所排除. 但是这并不意味着 GUT 错了，因为当然我们可以造出 $SO(10)$ 之类的 GUT. 实际上有时候人们丢掉一个理论并不是因为已经排除掉了所有的可能，而是大家已经对它失去信心了.

后来人们的注意力转移到超对称、超弦理论去了.

(4) Origin of Seed Fluctuations (涨落的源头？)：目前的宇宙当然是不均匀的，但是初期的宇宙很均匀，早期的小小涨落是怎么扩展到现在这个尺度的？这也是普通的大爆炸无法解决的.

---

当时的物理学家从问题 (3) 出发，想到如果在一个视界内生成了磁单极子，但是通过某一种机制使得这些磁单极子被“稀释”了，那么问题就消失了.

暴涨理论 (inflation，来源于经济学中的“通货膨胀”)：

在很短的时间内，宇宙膨胀了 $e^{60}$ 倍左右 ($10^{26}$)；同时有某种物理机制使得宇宙能够退出暴涨.

看起来就像是给大爆炸理论打了一个补丁，但是后来我们发现这个假说能够解决上面的四个问题.

考虑在暴涨前的一个区域，暴涨变大的是物理尺度，从这个角度来看，问题 (1) 就被解决了.

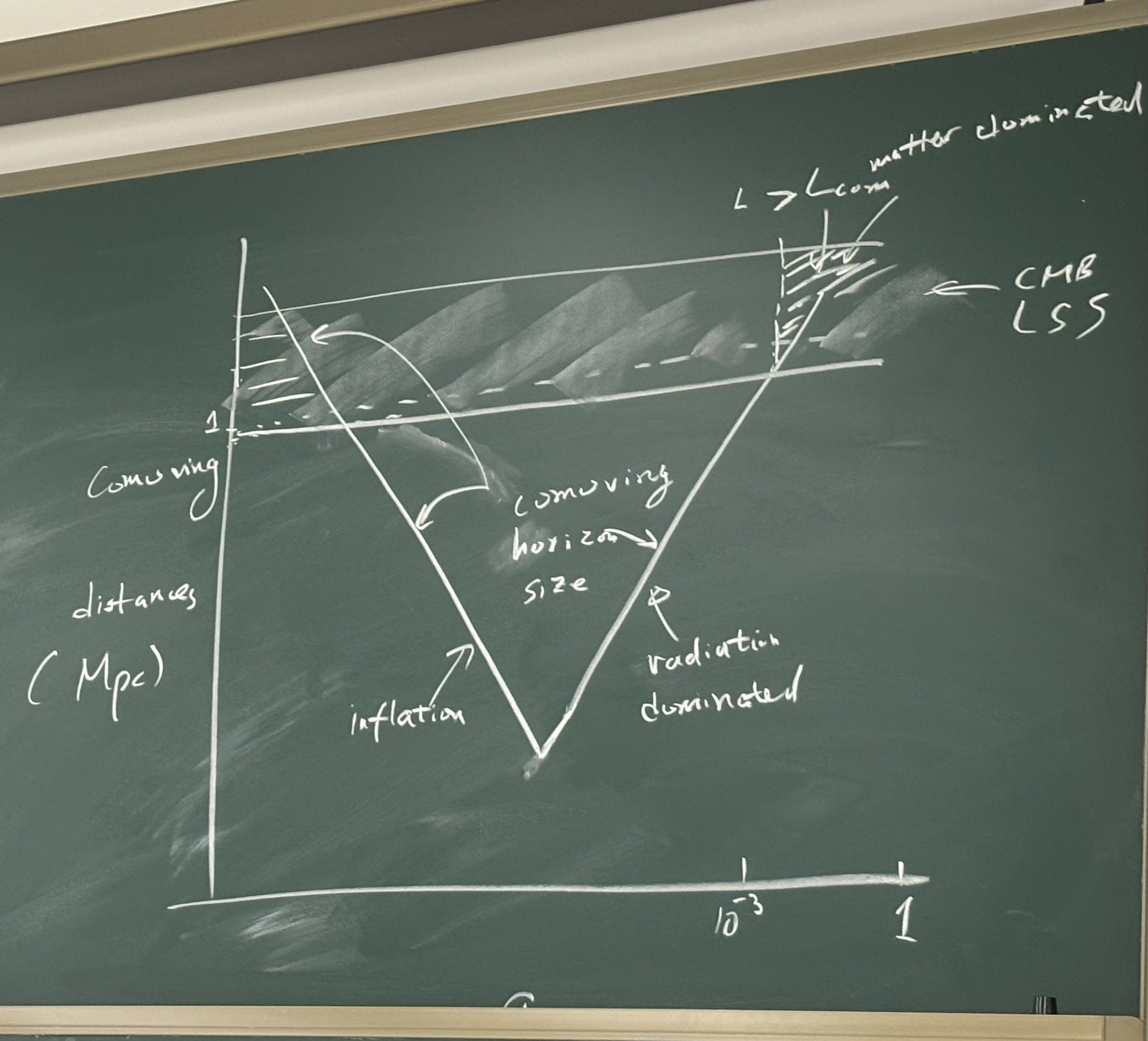
提示

不恰当的比喻：孙悟空画了一个圈围住唐僧和马，但是现在唐僧急剧膨胀，最后圈里面可能就只剩下一根马毛了.

暴涨使得 comoving horizon size 急剧减小，早期热平衡的两个区域在后期脱离开来，它们在脱离之前已经达到了热平衡，因此在较大的尺度上 CMB 是各向同性的，这就解释了问题 (2).

而问题 (4) 中的 Fluctuations 来源于早期的量子级别涨落，它们被暴涨所放大，成为了宏观可观测效应.

---

如何实现暴涨？

1981 年 Alan Guth 提出了暴涨，现在被称为 "old inflation"，他考虑的是下面的这种真空能分布：

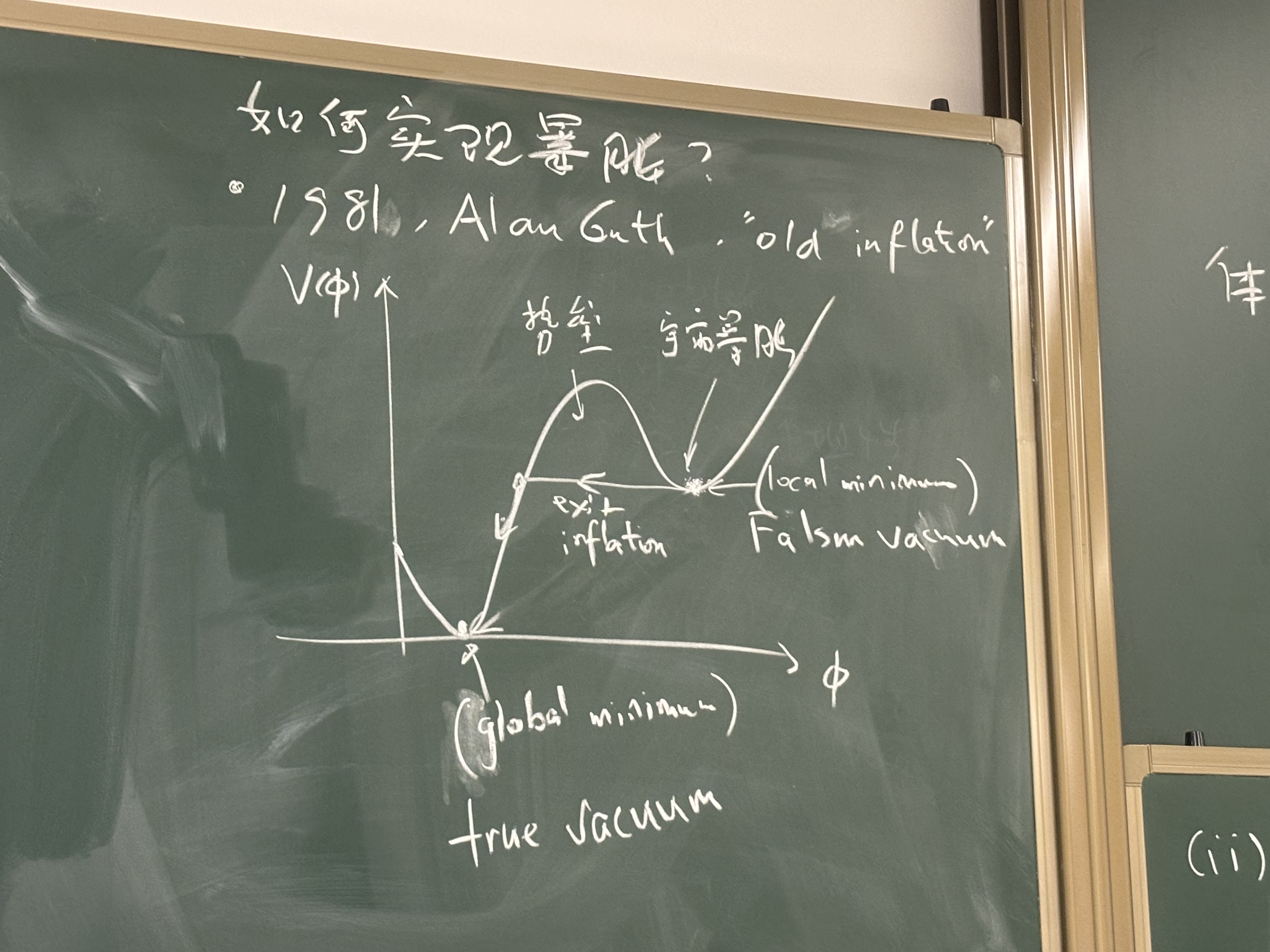
相当于宇宙处在“假真空”中时，相当于有一个暗能量在推动宇宙加速膨胀；当宇宙通过量子隧穿越过中间的势垒时，就会跳出 inflation，进入真真空.

但是这个模型存在问题：隧穿概率并不是整个宇宙各处相同的，宇宙各处退出暴涨的时间不同，会导致宇宙产生巨大的各向异性.

1982 - 1983 年，Andrei Lindei 提出了 slow - roll model：既然退出的方式有概率差异，为什么不让退出方式不是量子的，而是经典的呢？因此只需要把势垒放平即可.

后来 Starobinsky 声称他在 1980 年已经提出了暴涨，他通过 $R^2$ 修改引力模型，计算出来了一种暴涨机制，但是他并没有解释退出机制和如何解决上面四个疑难.

当然后面还有很多暴涨理论 (暴涨指的是一类理论)，比如 chaotic inflation 等等.

同时，Inflation 有一个竞争性的理论，要求脉动的宇宙存在，是 Paul Steindbhart 提出的，他在暴涨理论的建立过程中也有很大贡献.

更新日志

2026/9/9 05:47

查看所有更新日志

• d6df0-build(theme): theme update于 2026/9/9
• c3099-build(theme): update theme于 2026/2/25
• f85b5-build(theme): update theme to rc-168于 2025/10/9
• 395f7-feat(note): add cosmos note于 2025/5/5

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)

贡献者: physnya

上一页Lesson 10 宇宙演化的统计研究

下一页Lesson 13 线性微扰理论