Boltzmann 方程 & Saha 方程

物质 - 辐射相等的时刻 (matter - radiation equality)：

$$\rho_{M,0}=\Omega_M\rho_c\,,\quad\rho_{R,0}=\Omega_R\rho_c$$

而我们知道物质和辐射的密度与尺度因子 $a$ 的关系：

$$\rho_M=\rho_{M,0}\left(\frac{a}{a_0}\right)^{-3}=\rho_{M,0}\left(\frac{T}{T_{\gamma,0}}\right)^{3}\,,\quad\rho_R=\rho_{R,0}\left(\frac{a}{a_0}\right)^{-4}=\rho_{R,0}\left(\frac{T}{T_{\gamma,0}}\right)^{4}$$

将这两个量作比，得到

$$\frac{\rho_M}{\rho_R}=\frac{\Omega_M}{\Omega_R}\left(\frac{T}{T_{\gamma,0}}\right)^{-1}$$

当达到相等时刻时，$T=T_{EQ}$，解得：

$$T_{EQ}=T_{\gamma,0}\left(\frac{\Omega_M}{\Omega_R}\right)\approx10^{4}\text{ K}\sim1\text{ eV}$$

这里采用的是 $\Omega_M=0.7$，$\Omega_R=0.3$ 的数据. 上节课说到退耦的温度大约是 $10\text{ eV}$ 量级，和这个结果是自洽的. 还可以计算这时的红移：

$$1+z_{EQ}=\frac{a_{EQ}}{a_0}=\left(\frac{T_{EQ}}{T_{\gamma,0}}\right)^{-1}=\frac{\Omega_R}{\Omega_M}\approx3500$$

在 CMB 时，红移大约是 $1100$，温度约为 $0.3\text{ eV}$ 量级，因此我们可以说物质和辐射相等的阶段在 CMB 发生之前.

下面我们用 Boltzmann 方程 (non - equilibrium rate equation) 来仔细计算这个过程.

对于一个反应 $1+2\longleftrightarrow3+4$，我们可以写出：

$$a^{-3}\frac{\text{d}}{\text{d}t}(n_1a^3)=n_1^{(0)}n_2^{(0)}\braket{\sigma v}\left\{\frac{n_3n_4}{n_3^{(0)}n_4^{(0)}}-\frac{n_1n_2}{n_1^{(0)}n_2^{(0)}}\right\}$$

解释：

本来数密度就会随着尺度因子的变化而变化，所以我们将 $n$ 和 $a^3$ (体积限度) 乘在一起，保证所谓的“共动体积”中，只要没有其他变化，粒子数是不变的. 当然我们在 $\text{LHS}$ 还除了 $a^3$，这是出于量纲平衡的考虑.

for each species，there is

$$n_i=g_i\int\frac{\text{d}^3p}{(2\pi)^3}e^{-(E_i-\mu_i)/k_BT}$$

(相空间中的状态数积分，其中 $g_i$ 为简并度，$\mu_i$ 是化学势) 对于 $n^{(0)}_i$，

$$\begin{aligned} n_i^{(0)}&:=g_i\int\frac{\text{d}^3p}{(2\pi)^3}e^{-E_i/k_BT}=n_ie^{-\mu_i/k_BT}\\\\ &=\left\{\begin{array}{ll} g_i\left(\frac{m_iT}{2\pi}\right)^{3/2}e^{-m_ic^2/k_BT}&m_ic^2\gg k_BT\\\\ \frac{g_iT^3}{\pi^2}&m_ic^2\ll k_BT \end{array}\right. \end{aligned}$$

$\braket{\sigma v}$ 是 "thermally averaged cross - section"：

$$\begin{aligned} &=\frac{1}{n_1^{(0)}n_2^{(0)}}\int\frac{\text{d}^3p_1}{(2\pi)^3\cdot2E_1}\cdots\int\frac{\text{d}^3p_4}{(2\pi)^3\cdot2E_4}e^{-(E_1+E_2)/k_BT}(2\pi)^4\\\\ &\quad\quad\cdot\delta^{(3)}(\cdots) \end{aligned}$$

(我 * 我没抄完)

方程的含义大致是：反应的速率正比于反应的碰撞截面、反应左右两边的粒子数密度差异.

如果我们想要反应的 rate $n_2\braket{\sigma v}\gg1/t$ (expansion rate，宇宙膨胀速率)，这时我们还想要上述方程成立的方案是要求 $\{\cdots\}\to0$，这样 $\text{LHS}$ 就能远小于 $n_2\braket{\sigma v}$. 因此

$$\frac{n_3n_4}{n_3^{(0)}n_4^{(0)}}=\frac{n_1n_2}{n_1^{(0)}n_2^{0}}\text{ and }\frac{\text{d}}{\text{d}t}(a^3n_1)=0$$

也就是：反应的时间尺度远小于宇宙空间变化的时间尺度，宇宙膨胀的时间下看起来反应时刻处于平衡态，而 $\text{d}/\text{d}t$ 的值为零恰好对应了这一点 —— 宇宙中某处共动体积内粒子数不变，因为这个时间尺度下反应一直是平衡的.

在 CMB 研究领域，我们将这个方程 ($\{\cdots\}=0$) 称作 Saha 方程，其实它就是所谓的“化学势”相等 (当然在 BBN 的领域它还有一些别的名字之类的，但是核心就是化学势平衡).

当然我们要问：如果 $\text{d}/\text{d}t$ 一直是零，那么我们的反应怎么进行呢？实际上我们知道，宇宙的温度一直在缓慢变化，时间尺度和宇宙膨胀的尺度相似，因此整个反应长期处于“准静态”过程中，温度变化一点就进入新的平衡，我们的 Saha 方程也因此是平衡态方程.

接下来我们要应用这些方程来处理遇到的问题：

应用 - CMB

对于 CMB，反应是 $e+p\overset{\text{Recombination}}{\underset{\text{ionization}}{\longleftrightarrow}}\text{H}+\gamma$ ($E>13.6\text{ eV}$)，Saha 方程是：

$$\frac{n_en_p}{n_e^{(0)}n_p^{(0)}}=\frac{n_H}{n_H^{(0)}}$$

(光子化学势为零，不计算). 如果忽略 $\text{He}$，则 $n_e=n_p$，电离率为

$$\chi_e=\frac{n_p}{n_p+n_H}=\frac{n_e}{n_e+n_H}\,,\quad n_p+N_H=n_b$$

($n_b$ 为重子数密度)，解得 (非相对论情形下)：

$$\frac{n_en_p}{n_H}=\frac{\chi_e^2n_b}{1-\chi_e}\,,\quad\frac{n_e^{(0)}n_p^{(0)}}{n_H^{(0)}}=\frac{g_eg_p}{g_H}\left(\frac{m_em_p}{m_H}\right)^{3/2}\left(\frac{T}{2\pi}\right)^{3/2}e^{-B_1/k_BT}$$

我们知道，$g_e=2$，$g_p=2$ (俩 fermion)，它们合起来就是 $g_H=4$，同时只要不在指数上，我们还可以用近似 $m_H\approx m_p$，最后得到

$$\frac{n_e^{(0)}n_p^{(0)}}{n_H^{(0)}}\approx\left(\frac{m_eT}{2\pi}\right)^{3/2}e^{-B_1/k_BT}$$

Boltzmann 方程化为

$$\begin{aligned} a^{-3}\frac{\text{d}}{\text{d}t}(n_ea^3)&=n_e^{(0)}n_p^{(0)}\braket{\sigma v}\left\{\frac{n_H}{n_H^{(0)}}-\frac{n_en_p}{n_e^{(0)}n_p^{(0)}}\right\}\\\\ &=\braket{\sigma v}\left(\frac{n_e^{(0)}n_p^{(0)}}{n_H^{(0)}}\right)(1-\chi_e)n_b-\braket{\sigma v}\chi_e^2n_b^2\\\\ &=n_b\braket{\sigma v}\left\{(1-\chi_e)\left(\frac{m_eT}{2\pi}\right)^{3/2}e^{-B_1/k_BT}-\chi_e^2n_b\right\} \end{aligned}$$

而 $\text{LHS}$ 还能够写成 $n_b\frac{\text{d}\chi_e}{\text{d}t}$，在这样的情况下 Boltzmann 方程可以最终写成：

$$\frac{\text{d}\chi_e}{\text{d}t}=(1-\chi_e)\beta-\chi_e^2n_b\alpha^{(2)}$$

其中：

$$\beta:=\braket{\sigma v}\left(\frac{m_eT}{2\pi}\right)^{3/2}e^{-B_1/k_BT}$$

复合率 $\alpha^{(2)}=\braket{\sigma v}$. 我们知道，反应要有效，必须是一个光子先从 $n=+\infty$ 掉到 $n=2$ 态，在落到 $n=1$ 态，因为如果直接到 $1$ 能级，发射的光子又可以将电子电离出来，但是前面一种模式就能保证反应不会刚发生又回到初态，这种反应模式叫做 "case B recombination".

Saha 方程对应 $\text{RHS}=0$，也就是：

$$\frac{\chi_e^2}{1-\chi_e}=\frac{\beta}{n_b\alpha^{(2)}}=\frac{1}{n_b}\left(\frac{m_eT}{2\pi}\right)^{3/2}e^{-B_1/k_BT}$$

解的形式考察：

先不考虑 $\text{RHS}$ 前面的一坨因子，单纯考虑 $\exp$ 函数的效果，那么 $T\sim B_1$ 量级；

但是如果考虑前面的 pre - factor ($\propto T^{3/2}/n_b$)，就会“压低”这个 $T$ 的值，在 decoupling 之后整个 $T$ 值快速下降，转变点大约对应 $T\sim0.3\text{ eV}$.

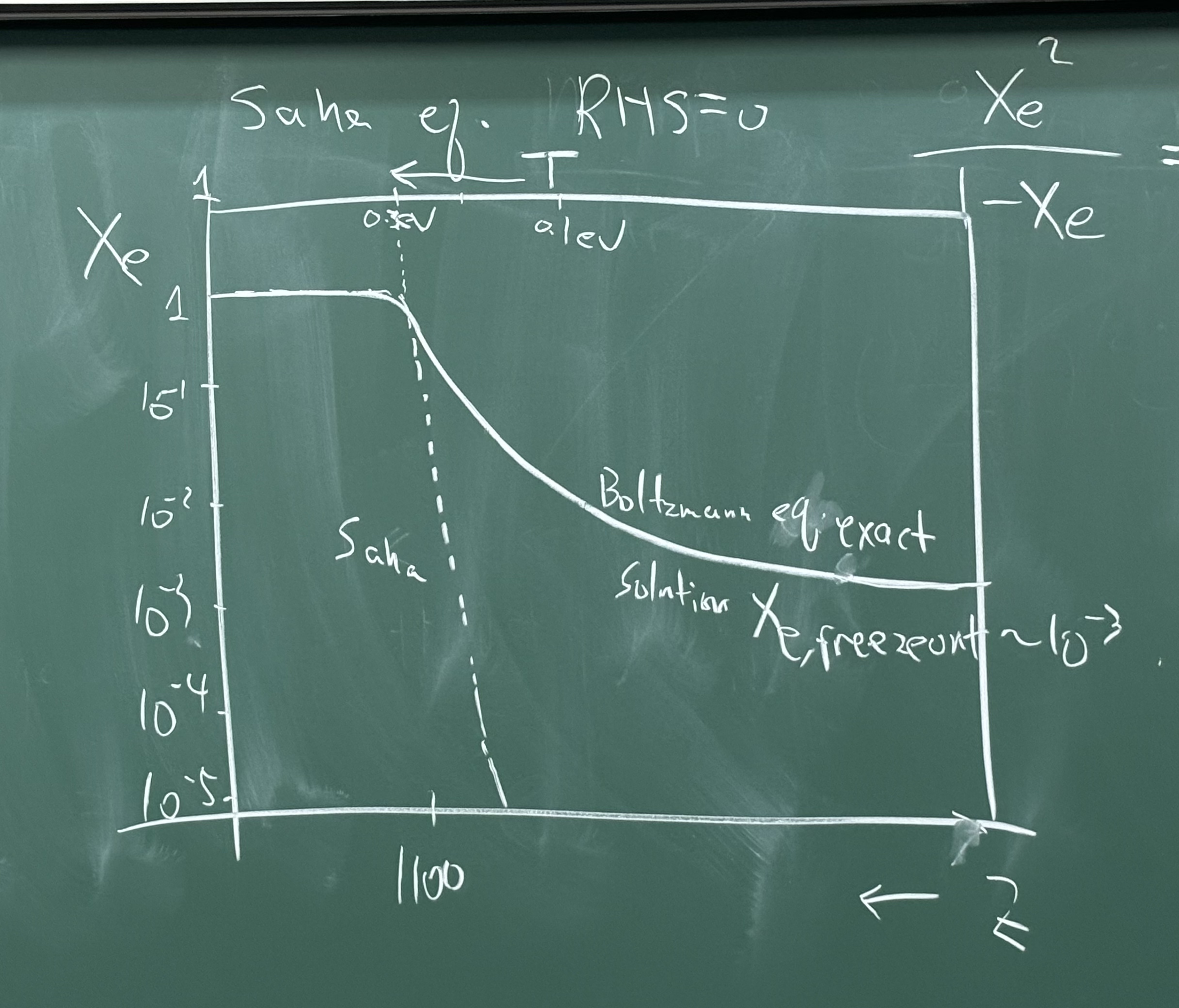
Saha 方程预言的是无限制地压低 (无限消耗氢元素). 如果严格解 Boltzmann 方程，转变点不会有太多变化 (这可能是个复杂的巧合)，但是最终 $T$ 值不会一直被压低，而是会存在一个残存的反应，因为 decoupling 之后反应不再平衡 (不再符合 Saha 方程)，且永远存在一些自由的电子.

两个方程给出的结果如下图：

问题：温度足够高时，我们觉得温度高时 $\chi_e$ 应该是接近于 $1$，但是 Saha 方程的 $\text{RHS}$ 有 $n_b\propto T^3$，因此 $\text{RHS}$ 在 $T\to\infty$ 时趋于 $0$，两边并不相等，这是为什么呢？

因为在 $T$ 非常高的情况下，应该换用相对论性的描述！

CMB 的偶极各向异性

(CMB dipole anisotropy)

老师上课画的抽象示意图

2025年4月21日

Planck 公式能够写成光子数密度的形式：(在 $\nu+\text{d}\nu$ 之间的光子数密度)

$$n(\nu)\text{d}\nu=\frac{8\pi\nu^2/c^3}{e^{h\nu/k_BT}-1}\text{d}\nu$$

我们想要改写成相空间的数密度的公式 (因为相空间体积元是一个 Lorentz 不变量、相应地，相空间数密度也是不变量)，因此先写出已知的关系：

$$N=N(\vec{x},\vec{p})\text{d}^3\vec{x}\text{d}^3\vec{p}\,,\quad|\vec{p}|=E/c=h_{p'}\nu/c$$

因此 $\text{d}^3p=4\pi|\vec{p}|^2\text{d}p=4\pi h^3_{p'}\nu^2/c^3\text{d}\nu$，$N_\gamma(\vec{x},\vec{p})=N_\gamma(p)$ (与位置和 $\vec{p}$ 方向无关). 所以相空间内的光子数表达式为

$$N_\gamma(p)=\frac{1}{h_{p'}^3}\frac{1}{e^{pc/k_BT}-1}$$

对于相对于 CMB 有运动的我们来说，要做一个 Lorentz boost，$|\vec{p}|=(1+\beta\cos\theta)|\vec{p}'|$ (这不就是 4 - momentum 变换吗……)

$$\begin{pmatrix} p_1\\p_2\\p_3\\|\vec{p}| \end{pmatrix}=\begin{pmatrix} 1&&&\\ &1&&\\ &&\gamma&\beta\gamma\\ &&\beta\gamma&\gamma \end{pmatrix}\begin{pmatrix} p_1'\\p_2'\\p_3'\\|\vec{p}'| \end{pmatrix}$$

这里得到地球系上面的光子数密度角分布：

$$N'_\gamma(p')=N_\gamma(p)=\frac{1}{h_{p'}^3}\frac{1}{\exp\left[\frac{\gamma(1+\beta\cos\theta)p'c}{k_BT}\right]-1}=\frac{1}{h_{p'}^3}\frac{1}{\exp\left[\frac{p'c}{k_BT'(\theta)}\right]-1}$$

于是温度角分布：

$$T'(\theta)=\frac{T}{1+\beta\cos\theta}\approx T(1-\beta\cos\theta)$$

恰好对应 Lagendre 展开中的 $l=1$ 多项式，也就是偶极项.

用球谐函数描述温度角分布：

$$T(\hat{n})=\sum_{l=0}^\infty\sum_{m=-l}^{+l} Y_{lm}(\hat{n})a_{lm}$$

球谐函数是什么？

在球面上建立无穷多的正交基矢，依据这些基矢将函数展开. 相当于将涨落分解为不同的阶数进行分析.

当然，随机性会体现在系数 $a_{lm}$ 中，为了滤去这种随机性，我们计算所谓功率谱 $c_l$：

$$\braket{a_{lm}a^*_{lm}}=\frac{2}{2l+1}\delta_{ll'}c_l$$

对于更小的 $l$，对应更大尺度的关联性质，而这些量都可以通过观测数据来很严格地计算出来. 因此原则上我们能通过观测量 fit 出功率谱的形式，以此来了解 CMB 中所蕴含的宇宙中的物质信息.

提示

以教室为例，最小尺度 (大 $l$ 处) 是间隔两个人的座位分布，这里会出现一个峰，因为大量的座位都是两个人挨着的；更小的 $l$ 处显然峰比较低，因为隔更多的人似乎找到下一个人的概率比较低，所以这种关联相对较弱.

更新日志

2025/10/9 02:50

查看所有更新日志

• f85b5-build(theme): update theme to rc-168于 2025/10/9
• f9d1b-feat: add cosmos notes于 2025/4/21
• 64ed5-feat: add cosmos notes于 2025/4/21

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)

贡献者: physnya

上一页Lesson 9 CMB 的特性

下一页Lesson 12 中微子脱耦 & 暴涨