菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 7 幂级数 & Taylor 展开

复制页面

约 2512 字大约 8 分钟

2025-5-13

幂级数

求收敛半径的方法：

  1. 根据 Cauchy 判别法，当

    lim⁡n→∞‾∣cn(z−a)n∣1/n<1\overline{\lim_{n\to\infty}}|c_n(z-a)^n|^{1/n}<1

    也就是

    ∣z−a∣<1lim⁡n→∞‾∣cn∣1/n|z-a|<\frac{1}{\overline{\underset{n\to\infty}{\lim}}|c_n|^{1/n}}

    时收敛，取大于时发散.

    这里，收敛半径是

    R=lim⁡‾n→∞∣1cn∣1/nR=\underset{n\to\infty}{\underline{\lim}}\left|\frac{1}{c_n}\right|^{1/n}

  2. 根据 d'Alembert 判别法，当

    ∣z−a∣<lim⁡n→∞∣cncn+1∣|z-a|<\lim_{n\to\infty}\left|\frac{c_n}{c_{n+1}}\right|

    时级数收敛.

前者的缺点是不好计算；后者则是要求极限一定存在，这并不是时时刻刻都满足的.

幂级数 ∑∞n=0cn(z−a)n\underset{n=0}{\overset{\infty}{\sum}}c_n(z-a)^n 的每一项都是 zz 的解析函数，Abel 定理告诉我们，幂级数在收敛圆内可以逐项求导，且得到的是一个在更小 (或者不变) 收敛圆上的幂级数.

那么收敛圆上的幂级数性质如何？

答案是：可能在收敛圆上处处发散，例如，

1+z+z2+⋯+zn+⋯1+z+z^2+\cdots+z^n+\cdots

也可能在收敛圆上的一部分点收敛，一部分点发散，例如

z1+z22+z33+⋯+znn+⋯\frac{z}{1}+\frac{z^2}{2}+\frac{z^3}{3}+\cdots+\frac{z^n}{n}+\cdots

(z≠1z\neq1 时发散，除了这一点以外处处收敛)

还可能在收敛圆上处处收敛，例如

z21⋅2+z32⋅3+z43⋅4+⋯+znn(n−1)+⋯\frac{z^2}{1\cdot2}+\frac{z^3}{2\cdot3}+\frac{z^4}{3\cdot4}+\cdots+\frac{z^n}{n(n-1)}+\cdots

/Remark/

能不能直接拆括号证明上述级数收敛？

证明收敛级数实际上不能拆括号，但是我们是在对部分和拆括号啊.

综上所述：不论哪种情况，幂级数的 和函数 在收敛圆上肯定有奇点 (因为找不到一个邻域，里面的点全部收敛)，但是即使在奇点，幂级数仍然有可能收敛.

值得注意的是，“和函数”和级数不是一个东西，我们强调的是和函数在收敛圆上有奇点. 比如上面第三个例子，在 z=1z=1 的时候，和函数实际上在支点，而支点必为奇点，这一点并不解析.

可惜的是上述命题我们暂时还无法证明.

/Theorem/ (Abel 第二定理)

如果幂级数 ∑∞n=0cn(z−a)n\underset{n=0}{\overset{\infty}{\sum}}c_n(z-a)^n 在收敛圆内收敛到 f(z)f(z)，并且级数在收敛圆周上某点 z0z_0 也收敛，和为 SS，则沿着收敛圆内的任意曲线趋向 z0z_0 点 (要求曲线和收敛圆上过 z0z_0 点的切线夹角大于 00)，f(z)f(z) 都一致地趋于 SS.

简而言之，求收敛圆上的和函数值时要先审敛.

/Proof/

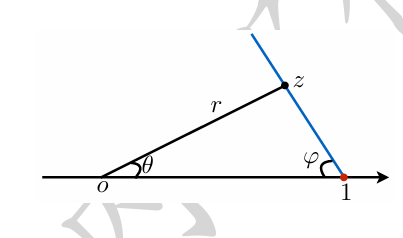
不失一般性，可以假设 a=0a=0，收敛半径 R=1R=1，以及收敛圆上的收敛点为 z=1z=1；另外，可以假设 ∑∞n=0cn=0\underset{n=0}{\overset{\infty}{\sum}}c_n=0，这个可以通过在 c0c_0 上附加一个常数做到.

记系数的部分和为 Sn=c0+c1+⋯+cnS_n=c_0+c_1+\cdots+c_n，所以：cnzn=(Sn−Sn−1)znc_nz^n=(S_n-S_{n-1})z^n，有

Sn(z)=(1−z)(S0+S1z+⋯+Sn−1zn−1)+SnznS_n(z)=(1-z)(S_0+S_1z+\cdots+S_{n-1}z^{n-1})+S_nz^n

再由 Snzn→0S_nz^n\to0，得到：

S(z)=(1−z)∑∞n=0SnznS(z)=(1-z)\underset{n=0}{\overset{\infty}{\sum}}S_nz^n

假设 n>N−1n>N-1 时，∣Sn∣<ε|S_n|<\varepsilon，则

∣S(z)∣≤∣1−z∣∣∑N−1n=0Snzn∣+ε∣1−z∣∑∞n=N∣zn∣=∣1−z∣∣∑N−1n=0Snzn∣+ε∣z∣N∣1−z∣1−∣z∣\begin{aligned} |S(z)|&\leq|1-z|\left|\underset{n=0}{\overset{N-1}{\sum}}S_nz^n\right|+\varepsilon|1-z|\underset{n=N}{\overset{\infty}{\sum}}|z^n|\\\\ &=|1-z|\left|\underset{n=0}{\overset{N-1}{\sum}}S_nz^n\right|+\frac{\varepsilon|z|^N|1-z|}{1-|z|} \end{aligned}

前面一项总之是有限的，但是难点在于后面那个等比级数. 在单位圆内，有 z=reiθz=re^{\text{i}\theta}，r<1r<1. 因此：

∣1−z∣=1+r2−2rcos⁡θ=(1−r)1+4r2sin⁡2θ2(1−r)2|1-z|=\sqrt{1+r^2-2r\cos\theta}=(1-r)\sqrt{1+\frac{4r^2\sin^2\frac{\theta}{2}}{(1-r)^2}}

如何估算根式部分的上界？Abel 第二定理说不能沿着切线方向，想到证明过程中应该用到角度：

代入得到：

rsin⁡φ=1sin⁡(θ+φ)⟹4r2sin⁡2θ2(1−r)2=cos⁡θ−cos⁡(θ+2φ)1+cos⁡(θ+2φ)\frac{r}{\sin\varphi}=\frac{1}{\sin(\theta+\varphi)}\Longrightarrow\frac{4r^2\sin^2\frac{\theta}{2}}{(1-r)^2}=\frac{\cos\theta-\cos(\theta+2\varphi)}{1+\cos(\theta+2\varphi)}

(其中用到和差化积 & 积化和差公式)

θ→0\theta\to0，φ<π/2\varphi<\pi/2，上式分母大于零，因此上式有界，也就是 ∣1−z∣<K(r−1)|1-z|<K(r-1)，证毕.

Abel 第二定理就是要求大家在求收敛圆上的值时一定要先审敛，比如 ∑∞n=0zn\underset{n=0}{\overset{\infty}{\sum}}z^n 在 z=−1z=-1 的值？

/Theorem/

设：

  1. f(t,z)f(t,z) 是 t,zt,z 的连续函数，t>at>a，z∈G‾z\in\overline{G}；
  2. 对于任何 t≥at\geq a，f(t,z)f(t,z) 是 G‾\overline{G} 上的单值解析函数；
  3. F(z)=∫a∞f(t,z)dtF(z)=\int_a^\infty f(t,z)\text{d}t 在 G‾\overline{G} 上一致收敛.

则 F(z)F(z) 在 GG 内部解析，且

F′(z)=∫a∞∂f(t,z)∂zdtF'(z)=\int_a^\infty\frac{\partial f(t,z)}{\partial z}\text{d}t

其证明就是 Weierstrass 定理.

应用这个定理时，需要判断无穷积分 (或瑕积分) 是否一致收敛，常用的判别法就是用一个 ϕ(t)\phi(t) 来判断，要求 ϕ(t)>∣f(t,z)∣\phi(t)>|f(t,z)|.

/Example/

求积分：

F(z)=∫0∞e−t2cos⁡(2zt)dtF(z)=\int_0^\infty e^{-t^2}\cos(2zt)\text{d}t

我们知道，

cos⁡z=cos⁡(x+iy)=cosh⁡ycos⁡x−isinh⁡ysin⁡x\cos z=\cos(x+\text{i}y)=\cosh y\cos x-\text{i}\sinh y\sin x

对这个模做一个估值：

∣cos⁡z∣=cosh⁡2ycos⁡2x+sinh⁡2y+sin⁡2x=cosh⁡2y−sin⁡2x≤cosh⁡2∣yt∣≤e2∣yt∣\begin{aligned} |\cos z|&=\sqrt{\cosh^2y\cos^2x+\sinh^2y+\sin^2x}\\\\ &=\sqrt{\cosh^2y-\sin^2x}\\\\ &\leq\cosh2|yt|\leq e^{2|yt|} \end{aligned}

这个似乎是无界的. 但是我们可以给它强行加一个“界”，要求函数呆在 zz 平面上的任意一个闭区域上，∣ℑ(z)∣<y0|\Im(z)|<y_0. 所以

∣e−t2cos⁡(2zt)∣<e−t2+2y0t\left|e^{-t^2}\cos(2zt)\right|<e^{-t^2+2y_0t}

而这个积分是收敛的，所以含参量的无穷积分一致收敛.

至于求积分：

F′(z)=−2∫0∞te−t2sin⁡(2zt)dt=e−t2sin⁡(2zt)∣0∞−2z∫0∞e−t2cos⁡(2zt)dt=−2zF(z)\begin{aligned} F'(z)&=-2\int_0^\infty te^{-t^2}\sin(2zt)\text{d}t\\ &=e^{-t^2}\sin(2zt)|^\infty_0-2z\int_0^\infty e^{-t^2}\cos(2zt)\text{d}t\\ &=-2zF(z) \end{aligned}

这是一个微分方程. 对于初始值，我们有：

F(0)=∫0∞∫0∞e−(x2+y2)dxdyF(0)=\int_0^\infty\int_0^\infty e^{-(x^2+y^2)}\text{d}x\text{d}y

换成极坐标，积分得到 π/2\sqrt{\pi}/2 (Gauss 积分). 最终答案：

F(z)=π2e−z2F(z)=\frac{\sqrt{\pi}}{2}e^{-z^2}

提示

讲到这里的时候突然有一阵震动.

“看来是中央空调开了，一年没开里边全是灰，结果全让咱们给吸干了. 为祖国健康吸灰…” —— 松神

解析函数的局域性展开

/Theorem/ (Taylor 展开)

函数 f(z)f(z) 在以 aa 为圆心的圆 CC 内部及 CC 上解析 (其实没必要在 CC 上解析)，则对于圆内部的任何 zz 点，f(z)f(z) 可以用幂级数展开为

f(z)=∑∞n=0an(z−a)nf(z)=\underset{n=0}{\overset{\infty}{\sum}}a_n(z-a)^n

其中，

an=12πi∮Cf(ζ)(ζ−a)n+1dζ=f(n)(a)n!a_n=\frac{1}{2\pi\text{i}}\oint_C\frac{f(\zeta)}{(\zeta-a)^{n+1}}\text{d}\zeta=\frac{f^{(n)}(a)}{n!}

围道 CC 取逆时针方向.

/Proof/

现在要来凑出这个幂级数.

对于任何一点，有

f(z)=12πi∮Cf(ζ)ζ−zdζf(z)=\frac{1}{2\pi\text{i}}\oint_C\frac{f(\zeta)}{\zeta-z}\text{d}\zeta

而，

1ζ−z=1(ζ−a)−(z−a)=1ζ−a∑∞n=0(z−aζ−a)n\frac{1}{\zeta-z}=\frac{1}{(\zeta-a)-(z-a)}=\frac{1}{\zeta-a}\underset{n=0}{\overset{\infty}{\sum}}\left(\frac{z-a}{\zeta-a}\right)^n

这个级数在 ∣(z−a)/(ζ−a)∣≤r<1|(z-a)/(\zeta-a)|\leq r<1 的区域中关于 ζ\zeta 一致收敛，因此可以逐项积分，也就是

f(z)=12πi∮C[∑∞n=0(z−a)n(ζ−a)n+1]f(ζ)dζ=∑∞n=0[12πi∮Cf(ζ)(ζ−a)n+1dζ](z−a)n=∑∞n=0an(z−a)n\begin{aligned} f(z)&=\frac{1}{2\pi\text{i}}\oint_C\left[\underset{n=0}{\overset{\infty}{\sum}}\frac{(z-a)^n}{(\zeta-a)^{n+1}}\right]f(\zeta)\text{d}\zeta\\ &=\underset{n=0}{\overset{\infty}{\sum}}\left[\frac{1}{2\pi\text{i}}\oint_C\frac{f(\zeta)}{(\zeta-a)^{n+1}}\text{d}\zeta\right](z-a)^n\\ &=\underset{n=0}{\overset{\infty}{\sum}}a_n(z-a)^n \end{aligned}

得证.

必需要注意：这里交换了积分和求导的顺序，所以中间验证了一致收敛性. 但是相对于实变函数，这里条件实际上放宽了，因为只需要解析函数，就足以保证 Taylor 级数收敛.

收敛范围：函数 f(z)f(z) 的奇点 (必须是不可去的，比如 sin⁡z/z\sin z/z 在 z=0z=0 是一个可去奇点) 完全决定了 Taylor 级数的收敛半径，设 bb 是 f(z)f(z) 离 aa 点最近的奇点，则收敛半径一般是 R=∣b−a∣R=|b-a|.

/Theorem/ (Taylor 展开的唯一性)

给定一个在圆 CC 内解析的函数，其 Taylor 展开是唯一的，展开系数 ana_n 是完全确定的.

提示

这时候大家对答案要是发现不一样，就要有自信：别人一定错了. Heisenberg 在美国核弹试爆之后仍然坚信是假消息，因为根据他的计算，核弹要 10 吨纯铀. 大家要像他一样自信.

注意：上述定理只在同一圆内、同一函数的情况下成立.

常用：

ez=∑n=0∞znn!=1+z+12z2+⋯ ,∣z∣<∞sin⁡(z)=∑n=0∞(−1)nz2n+1(2n+1)!=z−16z3+⋯ ,∣z∣<∞cos⁡(z)=∑n=0∞(−1)nz2n(2n)!=1−12z2+⋯ ,∣z∣<∞11−z=∑n=0∞zn=1+z+⋯ ,∣z∣<1\begin{aligned} e^z=&\sum_{n=0}^{\infty}\frac{z^n}{n!}=1+z+\frac{1}{2}z^2+\cdots\,,\quad|z|<\infty\\ \sin(z)=&\sum_{n=0}^{\infty}\frac{(-1)^nz^{2n+1}}{(2n+1)!}=z-\frac{1}{6}z^3+\cdots\,,\quad|z|<\infty\\ \cos(z)=&\sum_{n=0}^{\infty}\frac{(-1)^nz^{2n}}{(2n)!}=1-\frac{1}{2}z^2+\cdots\,,\quad|z|<\infty\\ \frac{1}{1-z}=&\sum_{n=0}^{\infty}z^n=1+z+\cdots\,,\quad|z|<1 \end{aligned}

对于其他的函数，尽量通过换元的方式回到这几个公式.

/Example/

11−3z+2z2=1(1−z)(1−2z)=A1−z+B1−2z\frac{1}{1-3z+2z^2}=\frac{1}{(1-z)(1-2z)}=\frac{A}{1-z}+\frac{B}{1-2z}

就能得到结果.

/Remark/

两个幂级数的和的收敛半径会怎么变？

某种程度上来说，肯定取最小的那个. 但是如果两个幂级数收敛半径一样大，没准就会出现收敛半径变大的情况：比如说 1/(1−z)1/(1-z) 和 1/(z−1)+1/(2−z)1/(z-1)+1/(2-z) …

也有可能可以通过逐项求导的方式得到新的幂级数：比如 1/(1−z)21/(1-z)^2 的展开.

更加有意思的例子是：

∑∞n=0k2\underset{n=0}{\overset{\infty}{\sum}}k^2 的求和，可以转化成 ∑∞n=0k2zk−1\underset{n=0}{\overset{\infty}{\sum}}k^2z^{k-1} 的求和，它是 ∑∞n=0kzk\underset{n=0}{\overset{\infty}{\sum}}kz^{k} 的求导，而后者再乘一个 z−1z^{-1}，就是 ∑∞n=0zk\underset{n=0}{\overset{\infty}{\sum}}z^k 的求导，最终是一个等比级数. 这在数学上称为生成函数法.

1/(1−z)21/(1-z)^2 的另一个求导方法：

lim⁡ε→01(1−z)(1+ε−z)=lim⁡ε→01ε∑∞n=0[1−1(1+ε)n+1]zn\lim_{\varepsilon\to0}\frac{1}{(1-z)(1+\varepsilon-z)}=\lim_{\varepsilon\to0}\frac{1}{\varepsilon}\underset{n=0}{\overset{\infty}{\sum}}\left[1-\frac{1}{(1+\varepsilon)^{n+1}}\right]z^n

用 L’Ho^pital\text{L'H}\hat{\text{o}}\text{pital} 法则即可.

更新日志

2025/10/9 02:50
查看所有更新日志
  • f85b5-build(theme): update theme to rc-168于
  • 645aa-feat(note): add writing note于
  • 9f124-perf(css): change img display于
  • fea9a-feat(note): add complex note于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)