菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 5 复变积分

复制页面

约 2382 字大约 8 分钟

2025-5-6

复变积分

/Theorem/ (单连通区域的 Cauchy 定理)

如果函数 f(z)f(z) 在单连通区域 G‾\overline{G} 中解析，则沿 G‾\overline{G} 中任何一个分段光滑的闭合围道 CC 有

∮Cf(z)dz=0\oint_Cf(z)\text{d}z=0

这里的 CC 也可以是 G‾\overline{G} 的边界.

/Remark/

要求 GG 是一个闭区域 (G‾\overline{G})，是因为强调有界性.

/Proof/

在更强的条件下证明这个定理：要求 f′(z)f'(z) 在 G‾\overline{G} 中连续. 在这个条件下应用 Green 公式：

∮C[P(x,y)dx+Q(x,y)dy]=∬S(∂Q∂x−∂P∂y)dxdy\oint_C[P(x,y)\text{d}x+Q(x,y)\text{d}y]=\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\text{d}x\text{d}y

在复变函数中，可以把复变积分拆开，得到：

∮C(u+iv)d(x+iy)=∮C(udx−vdy)+i∮C(udy+vdx)=−∬S(∂u∂y+∂v∂x)dxdy+∬S(∂u∂y+∂v∂x)dxdy\begin{aligned} \oint_C(u+\text{i}v)\text{d}(x+\text{i}y)&=\oint_C(u\text{d}x-v\text{d}y)+\text{i}\oint_C(u\text{d}y+v\text{d}x)\\ &=-\iint_S\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\text{d}x\text{d}y+\iint_S\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\text{d}x\text{d}y \end{aligned}

证毕.

/Remark/

后面发现导数连续的条件是不必要的. Green 函数的适配条件就是中间不能出现间断点，因为 Green 函数相当于人为引入了一个“洞”.

Goursat 提出了一个更好的证明：取三角形围道，令

I=∮Δf(z)dzI=\oint_\Delta f(z)\text{d}z

大三角形可以划分为四个全等的小三角形 (取三条中位线)，且有

I=∮Δ1f(z)dz+∮Δ2f(z)dz+∮Δ3f(z)dz+∮Δ4f(z)dzI=\oint_{\Delta_1}f(z)\text{d}z+\oint_{\Delta_2}f(z)\text{d}z+\oint_{\Delta_3}f(z)\text{d}z+\oint_{\Delta_4}f(z)\text{d}z

这四个围道积分一定有一个最大的，记为 MΔ(1)M_{\Delta^{(1)}}，同时记大三角形积分为 M=∣I∣M=|I|，有

MΔ(1)≥M4M_{\Delta^{(1)}}\geq\frac{M}{4}

无限细分，得到

MΔ(n)≥M4nM_{\Delta^{(n)}}\geq\frac{M}{4^n}

接下来估算 MΔ(n)M_{\Delta^{(n)}}：由区间套，必然存在一点 z0z_0 为所有 Δ→Δ(n)\Delta\to\Delta^{(n)} 内部的公共点，这一点在区域内，所以可导，因此 ∀ε>0\forall\varepsilon>0，∃δ(ε)\exist\delta(\varepsilon)，使得当 ∣z−z0∣<δ|z-z_0|<\delta 时满足

∣f(z)−f(z0)z−z0−f′(z0)∣<ε∣f(z)−f(z0)−f′(z0)(z−z0)∣<ε∣z−z0∣\left|\frac{f(z)-f(z_0)}{z-z_0}-f'(z_0)\right|<\varepsilon\\ |f(z)-f(z_0)-f'(z_0)(z-z_0)|<\varepsilon|z-z_0|

所以原来的小三角形积分为

∮Δ(n)f(z)dz=∣∮Δ(n)f(z)−f(z0)−f′(z0)(z−z0)∣≤ε∮∣z−z0∣∣dz∣≤ε(L(n))2\begin{aligned} \oint_{\Delta^{(n)}}f(z)\text{d}z&=|\oint_{\Delta^{(n)}}f(z)-f(z_0)-f'(z_0)(z-z_0)|\\ &\leq\varepsilon\oint|z-z_0||\text{d}z|\\ &\leq\varepsilon (L^{(n)})^2 \end{aligned}

Cauchy 定理的几个推论：

/Theorem/ (不定积分)

如果函数 f(z)f(z) 在单连通区域内解析，则

F(z)=∫z0zf(ζ)dζF(z)=\int_{z_0}^zf(\zeta)\text{d}\zeta

也在 GG 上解析.

/Proof/

设 zz 是 GG 中的一个点，有

ΔFΔz=F(z+Δz)−F(z)Δz=1Δz∫zz+Δzf(ζ)dζ\frac{\Delta F}{\Delta z}=\frac{F(z+\Delta z)-F(z)}{\Delta z}=\frac{1}{\Delta z}\int_{z}^{z+\Delta z}f(\zeta)\text{d}\zeta

所以：

∣ΔFΔz−f(z)∣=∣1Δz∫zz+Δz[f(ζ)−f(z)]dζ∣≤1∣Δz∣∫zz+Δz∣f(ζ)−f(z)∣⋅∣dζ∣\begin{aligned} |\frac{\Delta F}{\Delta z}-f(z)|&=|\frac{1}{\Delta z}\int_z^{z+\Delta z}[f(\zeta)-f(z)]\text{d}\zeta|\\ &\leq\frac{1}{|\Delta z|}\int_{z}^{z+\Delta z}|f(\zeta)-f(z)|\cdot|\text{d}\zeta| \end{aligned}

得证. 注意到这里必须要求路径是一条直线.

不定积分就由上面的定理来定义.

/Example/

计算积分：

∫abzndz ,n∈Z\int_a^bz^n\text{d}z\,,\quad n\in\mathbb{Z}

n≥0n\geq0 时，很简单，直接取原函数 zn+1/(n+1)z^{n+1}/(n+1).

n<−1n<-1 时也很简单，取单连通区域的时候绕开 z=0z=0 点就可以，这样我们发现，复连通区域中围道积分似乎也能为 00 (取一个挖掉 z=0z=0 点的区域，还是能作出不定积分)

n=−1n=-1，原函数是 ln⁡\ln，看起来似乎具有多值性，但是实际上这并不是多值的，因为一旦取定了单连通区域，就已经确定了辐角的绕向，而结果只与辐角的差有关系，所以取定了单连通区域，结果就已经确定了.

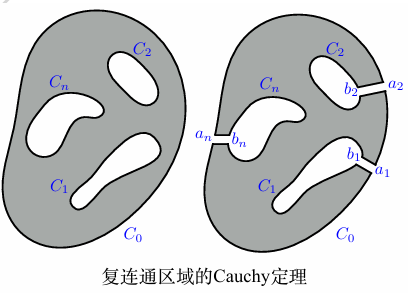
/Theorem/ (复连通区域的 Cauchy 定理)

如果 f(z)f(z) 是复连通区域 G‾\overline{G} 中的单值解析函数，则

∮C0f(z)dz=∑i=1n∮Cif(z)dz\oint_{C_0}f(z)\text{d}z=\sum_{i=1}^n\oint_{C_i}f(z)\text{d}z

其中，C0C_0 包含 Ci(i≠0)C_i(i\neq0)，CiC_i 是区域边界，走向全部取逆时针为正.

/Remark/

相当于取很多割线，将复连通区域变成单连通的区域：

/Example/

计算积分：

∮Czndz ,n∈Z\oint_Cz^n\text{d}z\,,\quad n\in\mathbb{Z}

CC 走向为逆时针方向.

这是一个重要的积分.

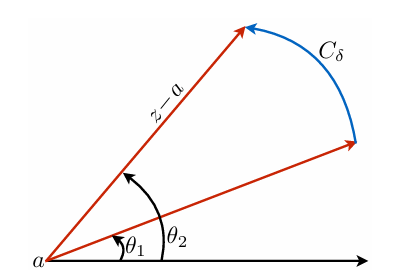
∮Czndz={0 ,n≥0 or z=0∉C∮∣z∣=εzndz+0=∫02πεn+1iei(n+1)θdθ={0 ,n<−12πεn+1i ,n=−1\begin{aligned} &\oint_Cz^n\text{d}z\\\\ &=\left\{\begin{array}{lr} 0\,,\quad n\geq0\text{ or }z=0\notin C\\\\ \oint_{|z|=\varepsilon}z^n\text{d}z+0=\int_0^{2\pi} \varepsilon^{n+1}\text{i}e^{\text{i}(n+1)\theta}\text{d}\theta=\left\{\begin{array}{ll} 0\,,\quad n<-1\\\\ 2\pi\varepsilon^{n+1}\text{i}\,,\quad n=-1 \end{array}\right. \end{array}\right. \end{aligned}

/Corollary/ (小圆弧引理)

如果函数 f(z)f(z) 在 z=az=a 点的邻域内部连续，并且当 θ1≤arg⁡(z−a)≤θ2\theta_1\leq\arg(z-a)\leq\theta_2，∣z−a∣→0|z-a|\to0 时，(z−a)f(z)(z-a)f(z) 一致地趋近于 kk，则

lim⁡δ→0∫Cδf(z)dz=ik(θ2−θ1)\lim_{\delta\to0}\int_{C_\delta}f(z)\text{d}z=\text{i}k(\theta_2-\theta_1)

其中 CδC_\delta 是以 z=az=a 为圆心，δ\delta 为半径，夹角为 θ2−θ1\theta_2-\theta_1 的圆弧，∣z−a∣=δ|z-a|=\delta，θ1≤arg⁡(z−a)≤θ2\theta_1\leq\arg(z-a)\leq\theta_2.

/Proof/

因为：

∫Cδdzz−a=i(θ2−θ1)\int_{C_\delta}\frac{\text{d}z}{z-a}=\text{i}(\theta_2-\theta_1)

(这其实就是我们上面 n=−1n=-1 的积分)

于是得到：

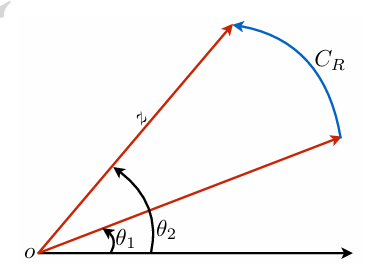
∣∫Cδf(z)dz−ik(θ2−θ1)∣≤ε(θ2−θ1)\left|\int_{C_\delta}f(z)\text{d}z-\text{i}k(\theta_2-\theta_1)\right|\leq\varepsilon(\theta_2-\theta_1)

/Corollary/ (大圆弧引理)

设 f(z)f(z) 在 ∞\infty 点的邻域内连续，当 θ1≤arg⁡z≤θ2\theta_1\leq\arg z\leq\theta_2，z→∞z\to\infty 时，zf(z)zf(z) 一致趋向 KK.

lim⁡R→0∫CRf(z)dz=iK(θ2−θ1)\lim_{R\to0}\int_{C_R}f(z)\text{d}z=\text{i}K(\theta_2-\theta_1)

CRC_R 是以原点为中心，RR 为半径，夹角为 θ2−θ1\theta_2-\theta_1 的圆弧.

证明过程和小圆弧引理类似.

/Theorem/ (Cauchy 积分公式)

f(z)f(z) 是有界区域 G‾\overline{G} 中的单值解析函数，G‾\overline{G} 的边界 CC 是分段光滑曲线，aa 为 GG 内一点，则

f(a)=12πi∮Cf(z)z−adzf(a)=\frac{1}{2\pi\text{i}}\oint_C\frac{f(z)}{z-a}\text{d}z

其中积分路径沿着 CC 正向.

提示

这意味着，复变函数携带的信息并不是二维的，而是一维的，边界和内部的函数值能够产生对应. 最近理论物理和宇宙学中的“共形场”就是基于这个简单的思想.

/Proof/

在 GG 内部做圆周 ∣z−a∣<r|z-a|<r，保持圆周在 GG 内部，根据复连通区域的 Cauchy 定理，有

∮Cf(z)z−adz=∮∣z−a∣=rf(z)z−adz\oint_C\frac{f(z)}{z-a}\text{d}z=\oint_{|z-a|=r}\frac{f(z)}{z-a}\text{d}z

但是这个结果不应该与 rr 的取值有关系，因此可以令 r→0r\to0，就证明了上述公式.

对于 aa 在 GG 外，需要假设 f(z)f(z) 在简单闭合围道 CC 上及 CC 外单值解析，这时可以用大圆弧引理，令 R→∞R\to\infty，得到无界的 Cauchy 积分公式：

12πi∮Cf(z)z−adz+K=f(a)\frac{1}{2\pi\text{i}}\oint_C\frac{f(z)}{z-a}\text{d}z+K=f(a)

其中 K=f(∞)K=f(\infty).

/Theorem/ (解析函数的高阶导数)

如果 f(z)f(z) 在 G‾\overline{G} 中解析，则任意阶高阶导数都存在，而且：

f(n)(z)=n!2πi∮Cf(ζ)(ζ−z)n+1dζf^{(n)}(z)=\frac{n!}{2\pi\text{i}}\oint_C\frac{f(\zeta)}{(\zeta-z)^{n+1}}\text{d}\zeta

其中 CC 是 G‾\overline{G} 的正向边界.

/Proof/

首先求 f′(z)f'(z)：

f(z+h)−f(z)h=12πi1h∮C[f(ζ)ζ−z−h−f(ζ)ζ−z]dζ=12πi∮Cf(ζ)(ζ−z−h)(ζ−z)dζ\begin{aligned} \frac{f(z+h)-f(z)}{h}&=\frac{1}{2\pi\text{i}}\frac{1}{h}\oint_C\left[ \frac{f(\zeta)}{\zeta-z-h}-\frac{f(\zeta)}{\zeta-z} \right]\text{d}\zeta\\ &=\frac{1}{2\pi\text{i}}\oint_C\frac{f(\zeta)}{(\zeta-z-h)(\zeta-z)}\text{d}\zeta \end{aligned}

令 h→0h\to0，证明了一阶情况.

但是我们交换了取极限和做积分的次序，所以要验证这是合法的操作，在这里有：

∮Cf(ζ)(ζ−z−h)(ζ−z)dζ−∮Cf(ζ)(ζ−z)2dζ=h∮Cf(ζ)(ζ−z−h)(ζ−z)dζ\oint_C\frac{f(\zeta)}{(\zeta-z-h)(\zeta-z)}\text{d}\zeta-\oint_C\frac{f(\zeta)}{(\zeta-z)^2}\text{d}\zeta=h\oint_C\frac{f(\zeta)}{(\zeta-z-h)(\zeta-z)}\text{d}\zeta

设 zz 到 CC 的最短距离为 δ\delta，同时因为 f(ζ)f(\zeta) 有界，令最大值为 MM，我们得到：

∮Cf(ζ)(ζ−z−h)(ζ−z)dζ−∮Cf(ζ)(ζ−z)2dζ≤M∣h∣δ2(δ−∣h∣)\oint_C\frac{f(\zeta)}{(\zeta-z-h)(\zeta-z)}\text{d}\zeta-\oint_C\frac{f(\zeta)}{(\zeta-z)^2}\text{d}\zeta\leq\frac{M|h|}{\delta^2(\delta-|h|)}

再令 h→0h\to0，发现这个交换极限和积分的操作是合法的.

/Example/ (Poisson 公式)

设 f(z)f(z) 在一个包含圆域 ∣z∣≤R|z|\leq R 的区域中解析，ζ=reiθ\zeta=re^{\text{i}\theta} 为圆内一点，0≤r<R0\leq r<R，证明下式成立：

f(ζ)=12π∫02πR2−r2R2−2Rrcos⁡(θ−φ)+r2f(Reiφ)dφf(\zeta)=\frac{1}{2\pi}\int_0^{2\pi}\frac{R^2-r^2}{R^2-2Rr\cos(\theta-\varphi)+r^2}f(Re^{\text{i}\varphi})\text{d}\varphi

(课后习题)

/Definition/ (Cauchy 型积分)

在分段光滑曲线 CC 上连续的函数 ϕ(ζ)\phi(\zeta) 构成的积分：

f(z)=12πi∫Cϕ(z)ζ−zdζf(z)=\frac{1}{2\pi\text{i}}\int_C\frac{\phi(z)}{\zeta-z}\text{d}\zeta

导数和 Cauchy 积分公式的高阶导数类似.

/Example/

计算积分

f(z)=12πi∮∣ζ∣=1ζ∗ζ−zdζ ,∣z∣≠1f(z)=\frac{1}{2\pi\text{i}}\oint_{|\zeta|=1}\frac{\zeta^*}{\zeta-z}\text{d}\zeta\,,\quad |z|\neq1

因为 ∣ζ∣=1|\zeta|=1，所以 ζ∗=1/ζ\zeta^*=1/\zeta！

但是不能直接用 Cauchy 积分公式，因为 zz 不一定在单位圆内部，而且 1/z1/z 这个函数在单位圆内部有奇点.

当 ∣z∣>1|z|>1，可以直接用积分公式，得到 −1/z-1/z；0<∣z∣<10<|z|<1 的时候，用无界的 Cauchy 积分公式，得到 00. ∣z∣=0|z|=0 时，就是上面说到的一个“重要的积分”，最终结果还是 00.

/Theorem/ (含参量积分的解析性)

设：

  1. f(t,z)f(t,z) 是 t,zt,z 的连续函数，t∈[a,b]t\in[a,b]，z∈G‾z\in\overline{G}；
  2. 对于 [a,b][a,b] 上的任何 tt，f(t,z)f(t,z) 是 G‾\overline{G} 上的单值解析函数.

则：

F(z)=∫abf(t,z)dtF(z)=\int_a^bf(t,z)\text{d}t

在 GG 内部解析，且

F′(z)=∫ab∂f(t,z)∂zdtF'(z)=\int_a^b\frac{\partial f(t,z)}{\partial z}\text{d}t

注意

感觉好多没听懂，PPT 上课还是太可怕了，要多练习一下 Inkscape，而且速度也不太跟得上来，还是 rime 的使用习惯没养成.

更新日志

2025/10/9 02:50
查看所有更新日志
  • f85b5-build(theme): update theme to rc-168于
  • 45160-feat(note): add complex note于
  • 0ebf7-feat(note): add writing note于
  • 0b9c2-feat(note): add complex note于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)