Lesson 4 多值函数 2

约 2443 字大约 8 分钟

2025-4-24

多值函数

(1) 根式函数： $w=\sqrt{z}$ (接着上节课的标题)

接着上节课来讲. 考虑下面一个简单的例子：

/Example/

试讨论 $w=\sqrt{(z-a)(z-b)}$ 的支点、割线画法和函数值的变化情况.
直接看是看不出来的，但是我们可以先“画圈”，得到 $a$ 、 $b$ 是支点 (转一圈某一个点相角变 $2\pi$ 、某一个点不变，开根号变成 $\pi$ )，而 $\infty$ 点不是支点.
于是最简单的割线画法是直接连接 $a$ & $b$ . 但是连线不一定是直的，根据问题的需要，我们可以画弯的、穿过无穷远点再穿回来的等等.

/Example/

课后的一个题目： $w=\sqrt{\sin z}$ 是不是多值函数？
宗量等于零的点有 $z=n\pi$ ， $n\in\mathbb{Z}$ . 显然我们直接画圈会遇到三角函数的无穷乘积问题，所以要换一种方式.
考虑： $\sin z=(z-n\pi)g(z)$ ，如果两边求导，则 $g'(z)(z-n\pi)+g(z)=\cos z$ ，可证明一定有一个 $z=n\pi$ 的邻域内部， $g(z)$ 恒不为零.
在这个小邻域里面画圈， $(z-n\pi)$ 辐角变化 $2\pi$ ，而 $g(z)$ 不变 (为什么？在 $g$ 平面里，这个圈对应一个闭合的曲线，而且一定不包含 $0$ 点)，所以 $z=n\pi$ 是一个支点.
$\infty$ 点呢？我们不能问这个问题. 因为找不到一个圈排除掉所有的 $z=n\pi$ 支点.

对于根式函数，画了割线之后，剩下的空间我们能够像解析函数一样讨论它们. 所以我们能够求导：

(\sqrt{z-a})'=\frac{1}{2\sqrt{z-a}}

显然分支点对于导函数都是奇点.

割线的缺点：

注意

它限制了辐角的变化范围，不能用来计算沿着非常复杂路径的问题.

我们的替代方案是，规定函数 $w$ 在某一点 $z_0$ 的值，并明确说明沿着某一条路径变化时，函数值没有跳变.

/Example/

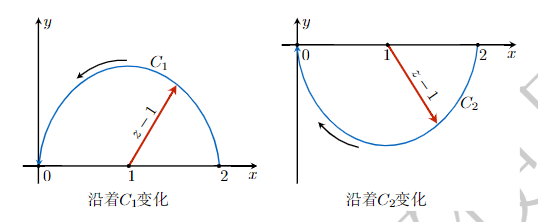
规定 $w=\sqrt{z-1}$ 的 $w(2)=1$ ，并规定沿着 $C_1$ 和 $C_2$ 两条路径，函数连续变化. 讨论这两条路径上的 $w(0)$ 值.
沿着 $C_1$ ， $\Delta\arg(z-1)=\pi$ ，而 $C_2$ 上 $\Delta\arg(z-1)=-\pi$ ，因此答案是：
$C_1$ 上的 $w(0)=e^{\text{i}\pi/2}=\text{i}$ ， $C_2$ 上的 $w(0)=e^{-\text{i}\pi/2}=-\text{i}$ .

这种方式可以使得宗量辐角不再受限，因而可以从一个单值分支运动到另一个单值分支 $\longrightarrow$ 将两个割开的 $z$ 平面粘接起来. 这种“剪一刀”再“粘起来”形成的、具有非常复杂拓扑结构的曲面，称为 Riemann 曲面.

实际上，多值函数并不定义在复平面上，而是定义在 Riemann 曲面上，在这个曲面上，多值函数不再成为多值函数，而是一个单值的多复变函数.

但是我们并不会使用 Riemann 曲面来做复变函数的问题，因为太过于困难，我们还是回到多值复变函数的范畴.

(2) 对数函数： $w=\ln z$

将 $z=re^{\text{i}\theta}$ 和 $w=u+\text{i}v$ 代进去，得到： $u=\ln r$ ， $v=\arg z$ ，多值性来源于宗量辐角的多值性. 对数函数多值性的表现则是 $w$ 的虚部.

导数：

w'=\frac{1}{z}

$w=\ln z$ 有无穷多分支，其 Riemann 曲面是无穷多叶的.

对数函数直接体现了辐角的多值性，因而各种多值函数都能通过对数函数表示，例如一般的根式函数 ( $\alpha$ 为任意复数)：

z^\alpha=e^{\alpha\ln z}(=e^{2\pi\alpha\text{i}}\cdot e^{\alpha\ln z})

反三角函数：

\begin{aligned} \arcsin z&=\frac{1}{\text{i}}\ln\left(\text{i}z+\sqrt{1-z^2}\right)\\\\ \arccos z&=\frac{1}{\text{i}}\ln\left(z+\sqrt{z^2-1}\right)\\\\ \arctan z&=\frac{1}{2\text{i}}\ln\frac{1+\text{i}z}{1-\text{i}z} \end{aligned}

/Remark/

怎么算出来的？直接解方程就得到了，但是这里的根号不是代数根号，因此直接包含了 $\pm$ 两种情况 (根式函数的多值性)，所以我们不需要考虑“二次”方程两个解的区别，直接取 $+$ .
反三角函数套了两层多值函数，因此也要分两层分析.
首先确定根式函数的两个支点是 $z=\pm1$ .
对于反正弦中的对数函数，似乎只有宗量为 $\infty$ 点才是分支点，也就是说只有一个支点.
但是实际上有两个，因为这两个 $\infty$ 分别在根式函数的两个单值分支上，所以有两个支点.
因此，割线应该是“无穷远点连接到 $-1\to1$ 线段 (根式函数的割线)，再连回去”的一条线 (像一个 T 形).

请弄清楚下面的例题：

/Example/

$w(z)=z^{-p}(1-z)^p$ ，给定上岸辐角为 $0$ ，割线是 $0\to1$ 的线段，求 $w(\text{i})$ ， $w(-\text{i})$ 和 $w(\infty)$ .
改写一下：
$w(z)=\left(\frac{1-z}{z}\right)^p$
这么一看， $\infty$ 不是支点，甚至是一个常点.
(1) 考虑从 $0\to1$ 的线段上某一点到 $\text{i}$ 这一点，有：
$\begin{aligned} \Delta\arg(1-z)&=\Delta\arg(z-1)=-\frac{\pi}{4}\\\\ \Delta\arg z&=\frac{\pi}{2}\\\\ \Delta w&=\Delta\arg(1-z)-\Delta\arg z=-\frac{3\pi}{4} \end{aligned}$
最后两个相减的原因是， $z$ 在分母上. 求模只需要把 $z=\text{i}$ 代入，得到
$|w(\text{i})|=\left|\frac{1-\text{i}}{\text{i}}\right|^p=2^p$
所以 $w(\text{i})=2^pe^{-3\pi\text{i}/4}$ .
(2) 先画一个路径出来！一个例子是从割线的左边绕过来：
$\begin{aligned} &\Delta\arg z=\frac{3\pi}{2}\\\\ &\Delta\arg(1-z)=\frac{\pi}{4}\\\\ &\Delta w=\Delta\arg(1-z)-\Delta\arg z=-\frac{5\pi}{4} \end{aligned}$
所以答案是 $w(-\text{i})=2^pe^{-5\pi\text{i}/4}$ .
(3) 考虑一条从 $0$ 走到 $\infty$ 的路径，得到 $w(\infty)=e^{p\pi\text{i}}$ .
/Remark/
其实取一个“绕开 $z=1$ 点走到 $\infty$ 点的路径”更好，这样 $z$ 的辐角不变 (只是在中间跳了一下又回来)，但是 $1-z$ 的辐角变了 $\pi$ ，这样更好思考一些.

这些多值函数的问题是最重要的部分，必须搞清楚.

注意

你要是搞清楚了就是 90 分往上，没搞清楚就是 60 分往下了.——松神

复变积分

在这一章，我们将看到复变函数最优美的一些性质.

复变积分是复平面上的线积分：

/Definition/

设 $C$ 是复平面上的曲线，函数 $f(z)$ 在 $C$ 上有定义，把曲线 $C$ 任意分为 $n$ 段，分点为 $z_0=A,z_1,z_2,\cdots,z_n=B$ . $\zeta_k$ 是 $z_{k-1}\to z_k$ 段上的任意一点，求和：
$\sum_{k=1}^nf(\zeta_k)(z_k-z_{k-1})=\sum_{k=1}^nf(\zeta_k)\Delta z_k$
若当 $n\to\infty$ ，使得 $\max|\Delta z_k|\to0$ ，此和数的极限存在，且与 $\zeta_k$ 的选取无关，则称这个极限值为函数 $f(z)$ 沿曲线 $C$ 的积分，记为：
$\int_Cf(z)\text{d}z=\lim_{n\to\infty}\sum_{k=1}^nf(\zeta_k)\Delta z_k$
/Remark/
曲线 $C$ 有方向，因为 $z_k-z_{k-1}$ 和 $z_{k-1}-z_k$ 是有区别的.
复变积分实际上是两个实变线积分的有序组合：
$\begin{aligned} \int_Cf(z)\text{d}z&=\int_C(u+\text{i}v)(\text{d}x+\text{i}\text{d}y)\\ &=\int_C(u\text{d}x-v\text{d}y)+\text{i}\int_C(v\text{d}x+u\text{d}y) \end{aligned}$
Stokes 公式：环积分和曲面积分的关联
$\oint_C(P\text{d}x+Q\text{d}y)=\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\text{d}x\text{d}y$

一些积分的性质：

线性性；
有限可加性；
有向性；
Cauchy - Schwartz 不等式：
$\left|\int_Cf(z)\text{d}z\right|\leq\int_C|f(z)||\text{d}z|$
这来自于复数的 Cauchy - Schwartz 不等式 (我们没证明，但是相当简单，高等微积分里面证明过).
若 $\underset{C}{\sup}|f(z)|=M$ ， $l$ 为 $C$ 的长度，则
$\left|\int_Cf(z)\text{d}z\right|\leq Ml$

一般情况下，复变积分的数值依赖于被积函数、端点位置 (上下限) 和积分路径.

/Example/

$\int_C\Re(z)\text{d}z$
按照以下三条路径：
(1) $0\to1\to1+\text{i}$ ；
(2) $0\to\text{i}\to1+\text{i}$ ；
(3) $0\to1+\text{i}$ .
(1) 有：
$\int_0^1x\text{d}x+\int_0^1\text{i}\text{d}y=\frac{1}{2}+\text{i}$
(2) 有：
$\int_0^1x\text{d}x=\frac{1}{2}$
(3) 有：
$\int_0^1(1+\text{i})\text{d}y=\frac{1}{2}(1+\text{i})$

看下面两个比较特殊的例子 (保守力！)：

/Example/

计算：
$\int_a^b\text{d}z\quad\&\quad\int_a^bz\text{d}z$
其中路径是任意的.
(1) 采用定义直接处理，有：
$\sum_{k=1}^n\Delta z_k=z_n-z_1\Longrightarrow\int_a^b\text{d}z=b-a$
和路径没关系.
(2) 这个更加困难，我们考虑取 $\zeta_k$ 的任意性，可以把 $\zeta_k$ 取为 $z_{k-1}$ 和 $z_k$ ，再取平均：
$\sum\zeta_k(z_{k}-z_{k-1})=\frac{1}{2}(z_{k}+z_{k-1})(z_k-z_{k-1})=\frac{1}{2}(z_k^2-z_{k-1}^2)$
所以答案是 $(b^2-a^2)/2$ .

现在我们想要问一个问题：积分在什么情况下与路径无关？

/Theorem/ (单连通区域的 Cauchy 定理)

/Definition/ (单连通区域 & 复连通区域)
在区域中作任何简单闭合围道，围道内的点都属于该区域，则为单连通区域.
反之则为复连通区域.
如果函数 $f(z)$ 在单连通区域 $\overline{G}$ 中解析，则沿着 $\overline{G}$ 中任何一个分段光滑的闭合围道 $C$ 有：
$\oint_Cf(z)\text{d}z=0$
这里的 $C$ 也可以是 $\overline{G}$ 的边界.