外观
Lesson 3 多值函数 1
约 2951 字大约 10 分钟
2025-4-22
解析函数
上节课我们讲到的比较重要的内容:C - R 方程 & 给定一个解析函数的实 / 虚部就能求虚 / 实部.
我们现在来看解析函数对实部和虚部的函数有什么限制:
不管怎么说,我们现在唯一知道的事实是 C - R 方程,因此先化简成需要的形式,
∂x2∂2u=∂x∂y∂2v,∂y2∂2u=−∂x∂y∂2v
因此利用 Laplace 算符写成 ∇2u=0,对 v 的要求也是一样的,这说明这两个函数必须是所谓的“调和函数” (这种函数的性质非常好,我们会在之后作很多说明).
因此也可以看出,解析性对函数的要求非常高,探讨解析函数的各种性质是复变函数论的中心话题.
函数的解析性总是和一块区域联系在一起:
/Definition/ (奇点)
函数不解析的点.
具体而言:无定义 / 有定义不连续 / 连续不可导 / 可导不解析.
问题:解析函数在导数为零的地方,4 个偏导数都是零,那么这里有什么样的性质?
解析函数 (不恒为常函数) 的实部和虚部在解析区域内无极值,导数为零的点只能是实部和虚部的鞍点 —— 这是由解析函数的性质决定的.
/Example/
w(z)=z2 的实部和虚部为 u=x2−y2,v=2xy,在 z=0 处两个函数都在鞍点.
当然,这个点可以是模的极值点.
问题:解析函数的实部沿着虚部为常数的曲线具有什么性质?
解析函数的实部沿着虚部为常数的曲线变化最快,反之亦然.
Bessel 函数中用到的最速下降法就是基于这个原理.
保角变换
有些同学学完 Feynman 系列的课程之后对保角变换非常有兴趣,我们简单科普一下:
众所周知,∇2φ=−ρ/ε0 (Poisson 方程). 当空间中没有电荷时,就变为 Laplace 方程,因此二维的调和函数就可以化为某种平面上的静电势进行处理.
实际上这并没有什么意义,因为二维 Laplace 方程并不好解. 但是某些情况下我们能够做一些变换使得这个问题被化简为更好解决的情况.
所谓保角变换是将 z=x+iy 映射到 w=u+iv 上面去,这个变换具有保角性 / 共形性:
/Proof/
考虑解析函数的微分:Δw=w′(z)Δz,这个微分表明,将 z 空间中的一个任意矢量 Δz 映射到 w 空间内,只是相乘了一个复数而已,相当于将模放大 ∣w′(z)∣ 倍,然后旋转 argw′(z) 角度,这两个量都和 Δz 无关 (仅仅和 z 有关).
因此这个变换是保角的.
举一个例子:
/Example/
无限大导体板对折成 θ,一无限长线电荷平行导体板中间的折线放置,求静电场.
一般而言,我们只能用电像法做 θ 整除 π 的情况. 但是用保角变换,可以做任意情况. 考虑原空间是 z 平面,用变换函数 w(z)=zπ/θ 进行变换.
⟹ 折叠的导体板被展开成无限大平板,这下就能计算结果了.
/Remark/
为什么能这么做?保角变换不改变解析性,也就不改变 Laplace 方程.
需要对线电荷的位置和大小做怎样的调整?(Laplace 方程在有电荷的位置不成立) 位置按照 w(z),但是电荷大小不变.
有人会问:不是说好的“保角”吗?为什么导体板被展开了?因为保角仅仅对解析的区域成立,保角变换的一大精髓就是巧妙地设置奇点的位置来产生绝妙的效果.
/Theorem/ (Riemann 存在定理)
可证明 (肯定非常难),在扩充的复平面上的两块单连通的区域之间,一定存在唯一的保角变换建立两者之间的联系.
再来一个例题:
/Example/
电荷均匀分布的无限长线电荷与半径为 a 的无限长接地导体圆柱平行放置,求静电场.
这问题的核心就是像电荷的位置和大小.
保角变换 w(z)=b+za2 (不知道我是不是抄错了)
保角变换的局限性 (非常明显):
- 只适用于二维问题;
- 找这个映射非常困难,只知道存在这种映射;
- (u,v)→(x,y) 的变换关系一般非常复杂.
提示
这也是 Feynman 书的特点,他每次搞懂了一个问题,就用一种异于常人的方法做出来,让你觉得他很厉害;但是这不是做科研的正常道路. 因此 Landau 的书就很受推崇,因为他真的在教你科研的道路.
在学习不同人写的书时,也要用不同的思维.
第一章结尾的一个问题:
P=sinnπsinn2π⋯sinn(n−1)π=?
这个想法非常奇怪.
我们考虑上面的每个因子都是 xn=1 的根. (但是实际上差了一个 2,之后我们会解决这个问题)
xn−1=0,xk=exp(n2πki),因式分解:
x−1xn−1⟹n=xn−1+⋯+1=k=1∏n−1(x−xk)=k=1∏n−1(1−en2πki)=∏{1−[cosn2πk+isinn2πk]}=∏(2sin2nπk−2isinnπkcosnπk)=∏2sinnπk∏[sinnπk−icosnπk]
其中后面一部分取模,就得到:
n=2n⋅P⋅1
所以原来的乘积是 P=n/2n.
初等函数 & 多值函数
初等函数
(1) 幂函数:zn
当 n∈N 时,zn 全平面解析;当 n∈Z+ 时,z=∞ 为奇点;
当 n∈Z−,zn 除了 z=0 外处处解析,在 z=∞ 也解析;
导数:(zn)′=nzn−1.
由此还可以定义有理函数 P(z)/Q(z).
问题:00 是多少?
这是典型的不定式,取决于取极限的方式.
(2) 指数函数:ez
定义:ez=ex+iy=ex⋅eiy=ex(cosy+isiny).
“指数函数相乘等于指数相加”.
全平面解析 (不包含 ∞ 点,事实上我们可以证明在扩充复平面上全平面解析的函数只能是常函数).
周期性,周期为 2πi.
(3) 三角函数:sinz,cosz
推广 Euler 公式,可以用复指数函数定义三角函数:
sinz=2ieiz−e−iz,cosz=2eiz+e−iz
也可以写成实部和虚部的形式 (以 cosz 为例):
cosz=coshycosx−isinhysinx
全平面解析,有
(sinz)′=cosz,(cosz)′=−sinz
周期为 2π,z=∞ 为唯一奇点. 同时注意,模不一定小于 1.
sin2z+cos2z=1.
问题:实数域内的恒等式在复数域内仍然成立是巧合吗?
这是解析函数的独特特性!
(4) 双曲函数:sinhz,coshz
也通过复指数函数定义:
sinhz=2ez−e−z,coshz=2ez+e−z
简单的关系就是 isinh(iz)=sinz,cosh(iz)=cosz.
多值函数
这是最重要的部分
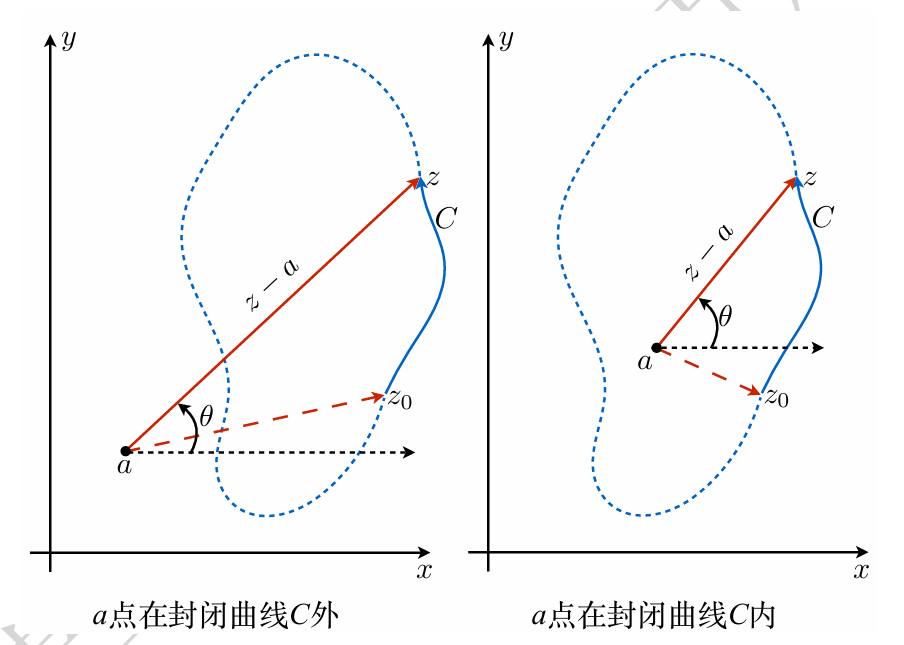
(1) 根式函数:z−a.
/Definition/
给定一个自变量 z,凡是满足 z2=w 的都是 w(z) 的函数值.
为了更清楚地看出多值函数地性质,我们写成 w=z−a 来进行分析. 称 z−a 为 宗量,z 为自变量. 用极坐标:
z−a=reiθ,w=ρeiφ
我们知道,ρ=r,且 2φ=θ+2nπ,于是多值性就来源于这里的 φ=θ/2+nπ.
- 根式函数的多值性来源于 宗量 的辐角多值性
实变函数里这个问题简单的点在于我们能够比较大小,因此可以规定大的那一个是正根,我们取函数值为这个量;但是复变函数不可以比较大小,我们没办法说哪个是正的.
同时,规定好 z 平面上的某一点 arg(z−a) 值,然后研究 z 沿着一条曲线连续变化时,相应的 w 的变化,如果曲线闭合,那么辐角应该也要能够变回来. 但是如果 z−a 的 a 点在曲线内部,z−a 转一圈,辐角增加 2π,那么 z−a 就多了一个负号,z−a 这个函数甚至沿着这个曲线都不连续.
如图:
(事实上自旋 - 1/2 就满足转一圈变一次的特性)
a 点在 w=z−a 中有重要的特性:
- z 绕着 a 转一圈 (考虑“翻过来”,也就是绕着 ∞ 点走了一圈,我们原地走一圈就能绕着除了中国以外的所有国家一圈),函数值变化一个负号;
- z 不绕着 a 转一圈,函数值不跳变.
a 点和 ∞ 点称为函数的分支点 (简称支点). 当然,绕着俩支点走一圈,函数值不跳变.
如何理解绕无穷远点一圈?
考虑一个足够大的圆,包含所有有限远点,绕着这个点转一圈即可.
如何判断支点?
针对根式函数来说,先确定宗量为 0 or ∞ 的点,然后取足够小的“圈”转一圈来判断是不是支点.
支点可不可以只有一个?
不可能,因为只要有一个支点,“翻过来” ∞ 点也就是支点.
可不可以没有支点?
可以,比如 w=z2. 这里 w=±z 所以多值,但是绕着任何可能的支点转一圈不会跳变.
多值函数的单值分支:我们可以强行规定辐角范围,以此来找到单值的分支.
/Example/
设 w=z−1,规定 0≤arg(z−1)<2π,求 w(2),w(i),w(0),w(−i).
显然 w(2)=1,w(i)=21/4e3πi/8,……
在规定 0≤arg(z−a)<2π 的情况下,w 被限制在上半平面,相当于如图:
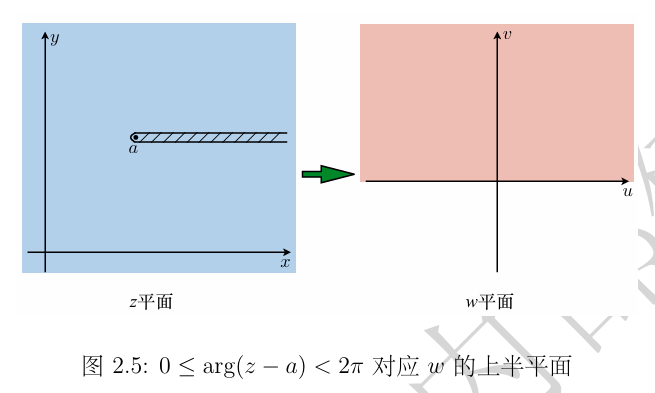
图 1
2025年4月22日
同理,规定 2π∼4π 的情况下,w 在下半平面,如图:
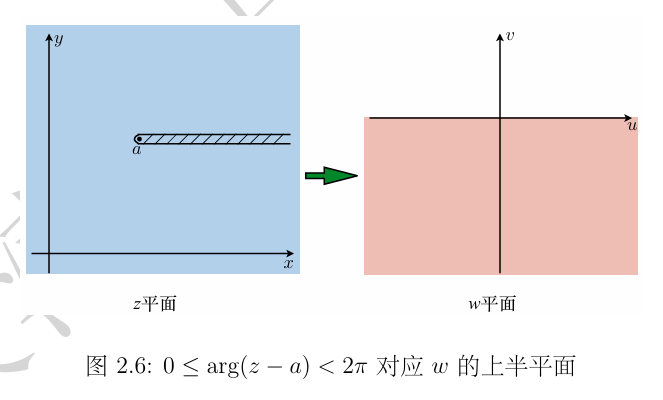
图 2
2025年4月22日
这种“规定辐角范围”的模式,相当于在两个支点之间做了一条割线,使得“绕圈”没办法绕过任何一个支点.
画割线的基本原则: 割线必须起始于支点并且终止于支点,每个支点至少有一条割线和它相连,画割线要尽量简单并且方便于问题的研究. 割线画好后 z 的任意连续变化 (不能跨越割线) 不会导致函数值的歧义.
更新日志
2025/10/9 02:50
查看所有更新日志
f85b5-build(theme): update theme to rc-168于80ce5-feat: add complex note于