菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 14 相关特殊函数

复制页面

约 2146 字大约 7 分钟

2025-6-5

Γ 函数

基本性质：

(1) Γ(1)=1\Gamma(1)=1.

(2) 递推关系：Γ(z+1)=zΓ(z)\Gamma(z+1)=z\Gamma(z).

/Proof/

用最简单的式子写出来：

Γ(z+1)=∫0∞tze−tdt=−tze−t∣0∞+z∫0∞tz−1e−tdt=z∫0∞tz−1e−tdt=zΓ(z)\begin{aligned} \Gamma(z+1)&=\int_0^\infty t^ze^{-t}\text{d}t\\ &=-t^ze^{-t}|^\infty_0+z\int_0^\infty t^{z-1}e^{-t}\text{d}t\\ &=z\int_0^\infty t^{z-1}e^{-t}\text{d}t=z\Gamma(z) \end{aligned}

得证.

这一证明是在右半平面做的，但是等式两边都能解析延拓，所以在全平面成立.

/Corollary/

由这一性质，阶乘可以用 Γ\Gamma 函数表达，n!=Γ(n+1)n!=\Gamma(n+1).

注意

一定要注意 (7/2)!(7/2)! 这种符号的含义，有可能是连乘，也有可能指的是 Γ(9/2)\Gamma(9/2). 这两种是有区别的，相差一个 π\sqrt{\pi}，不同的书籍不同.

同时，我们能够解析延拓：

Γ(z)=Γ(z+1)z=Γ(z+2)z(z+1)\Gamma(z)=\frac{\Gamma(z+1)}{z}=\frac{\Gamma(z+2)}{z(z+1)}

这个函数的定义域比右半平面宽一点，但是多了几个奇点. 按照这样的方式可以把定义域递归地往左推.

要记住的一个值：Γ(1/2)=π\Gamma(1/2)=\sqrt{\pi}.

(3) 互余宗量定理：

Γ(z)Γ(1−z)=πsin⁡πz≠0\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin\pi z}\neq0

由此可以发现，Γ\Gamma 函数在全平面无零点，这意味着其倒函数全平面无奇点.

(4) Γ\Gamma 函数的围道积分表示：

如图所示的围道：

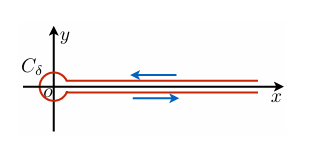
得到：

I=(e2πiz−1)∫0∞tz−1e−tdt=2ieπizsin⁡πzΓ(z)I=(e^{2\pi\text{i}z}-1)\int_0^\infty t^{z-1}e^{-t}\text{d}t=2\text{i}e^{\pi\text{i}z}\sin\pi z\Gamma(z)

也就是

Γ(z)=−12isin⁡πz∫∞(0+)(−t)z−1e−tdt ,∣arg⁡(−t)∣<π\Gamma(z)=-\frac{1}{2\text{i}\sin\pi z}\int_\infty^{(0+)}(-t)^{z-1}e^{-t}\text{d}t\,,\quad|\arg(-t)|<\pi

这个公式在 z∈Zz\in\mathbb{Z} 处不成立，但是可以延拓到全平面.

如果用互余宗量定理，得到无限制的定义：

1Γ(1−z)=−12πi∫∞(0+)(−t)z−1e−tdt ,∣arg⁡(−t)∣<π\frac{1}{\Gamma(1-z)}=-\frac{1}{2\pi\text{i}}\int_\infty^{(0+)}(-t)^{z-1}e^{-t}\text{d}t\,,\quad|\arg(-t)|<\pi

(5) 倍乘公式 (不用记忆，因为没什么必要)：

Γ(2z)=22z−1π−1/2Γ(z)Γ(z+12)\Gamma(2z)=2^{2z-1}\pi^{-1/2}\Gamma(z)\Gamma\left(z+\frac{1}{2}\right)

(6) Γ\Gamma 函数的渐近展开，即 Stirling 公式：当 ∣z∣→∞|z|\to\infty，∣arg⁡z∣<π|\arg z|<\pi 时，有

Γ(z+1)∼2πz(ze)z{1+112z+1288z2+⋯ }ln⁡Γ(z+1)∼(z+12)ln⁡z−z+12ln⁡(2π)+112z+⋯\begin{aligned} \Gamma(z+1)&\sim\sqrt{2\pi z}\left(\frac{z}{e}\right)^z\left\{1+\frac{1}{12z}+\frac{1}{288z^2}+\cdots\right\}\\\\ \ln\Gamma(z+1)&\sim\left(z+\frac{1}{2}\right)\ln z-z+\frac{1}{2}\ln(2\pi)+\frac{1}{12z}+\cdots \end{aligned}

常用结果是：ln⁡n!≈nln⁡n−n\ln n!\approx n\ln n-n.

/Proof/ (Stirling 公式)

令 t=zxt=zx，得到

Γ(z+1)=z∫0∞e−z(x−ln⁡x)+zln⁡zdx=zz+1∫0∞e−z(x−ln⁡x)dx\begin{aligned} \Gamma(z+1)&=z\int_0^\infty e^{-z(x-\ln x)+z\ln z}\text{d}x\\ &=z^{z+1}\int_0^\infty e^{-z(x-\ln x)}\text{d}x \end{aligned}

分析 y(x)=x−ln⁡xy(x)=x-\ln x 在 x=1x=1 附近的性质，得到

y(x)=x−ln⁡x∼1+(x−1)22y(x)=x-\ln x\sim1+\frac{(x-1)^2}{2}

所以得到证明：

∫0∞e−z(x−ln⁡x)dx∼e−z∫−∞∞e−zx2/2dx=2πze−z\int_0^\infty e^{-z(x-\ln x)}\text{d}x\sim e^{-z}\int_{-\infty}^\infty e^{-zx^2/2}\text{d}x=\sqrt{\frac{2\pi}{z}}e^{-z}

得到了渐近展开

Γ(z+1)∼2πz(ze)z\Gamma(z+1)\sim\sqrt{2\pi z}\left(\frac{z}{e}\right)^z

/Remark/

这个代换的方法在渐近分析中常用.

(7) 外氏无穷乘积：

1Γ(z)=zeγz∏n=1∞{(1+zn)e−z/n}\frac{1}{\Gamma(z)}=ze^{\gamma z}\prod_{n=1}^\infty\left\{\left(1+\frac{z}{n}\right)e^{-z/n}\right\}

Beta 函数

提示

正体 B\Beta 是 β\beta 的大写.

/Definition/ (B\Beta 函数)

由第一类 Euler 积分定义：

B(p,q)=∫01tp−1(1−t)q−1dt ,ℜ(p),ℜ(q)>0\Beta(p,q)=\int_0^1t^{p-1}(1-t)^{q-1}\text{d}t\,,\quad\Re(p),\Re(q)>0

令 t=sin⁡2θt=\sin^2\theta 得到另一表达式：

B(p,q)=2∫0π/2sin⁡2p−1θcos⁡2q−1θdθ\Beta(p,q)=2\int_0^{\pi/2}\sin^{2p-1}\theta\cos^{2q-1}\theta\text{d}\theta

注意到关于 p,qp,q 是对称的.

B\Beta 函数能够用 Γ\Gamma 函数表示，

B(p,q)=Γ(p)Γ(q)Γ(p+q)\Beta(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}

/Proof/

将 Γ\Gamma 函数写成：

Γ(p)=∫0∞e−ttp−1dt=2∫0∞e−x2x2p−1dx\Gamma(p)=\int_0^\infty e^{-t}t^{p-1}\text{d}t=2\int_0^\infty e^{-x^2}x^{2p-1}\text{d}x

同理 Γ(q)=γ(y)\Gamma(q)=\gamma(y). 相乘：

Γ(p)Γ(q)=4∫0∞∫0∞e−(x2+y2)x2p−1y2q−1dxdy\Gamma(p)\Gamma(q)=4\int_0^\infty\int_0^\infty e^{-(x^2+y^2)}x^{2p-1}y^{2q-1}\text{d}x\text{d}y

转为极坐标，得证 Γ(p)Γ(q)=Γ(p+q)B(p,q)\Gamma(p)\Gamma(q)=\Gamma(p+q)\Beta(p,q).

可以利用此关系：

  • 将 B\Beta 函数延拓到 p,qp,q 的全平面.
  • 发现 p,qp,q 的对称性.
  • 补充证明互余宗量定理和倍乘公式.

/Proof/ (互余宗量定理)

用到 B(z,1−z)=Γ(z)Γ(1−z)\Beta(z,1-z)=\Gamma(z)\Gamma(1-z)，LHS 用留数定理，直接得证.

/Proof/ (倍乘公式)

公式中含有 Γ(z+1/2)\Gamma(z+1/2)，Γ(z)\Gamma(z) 和 Γ(2z)\Gamma(2z)，所以写：

Γ(z)Γ(1/2)Γ(z+1/2)=2z2z−1∫01(1−t)z−1tz−1dt\frac{\Gamma(z)\Gamma(1/2)}{\Gamma(z+1/2)}=2z^{2z-1}\int_0^1(1-t)^{z-1}t^{z-1}\text{d}t

另外，

Γ(z)Γ(z)Γ(z)=B(z,z)=∫01(1−t)z−1tz−1dt\frac{\Gamma(z)\Gamma(z)}{\Gamma(z)}=\Beta(z,z)=\int_0^1(1-t)^{z-1}t^{z-1}\text{d}t

两者之间的联系是：t=(1+x)/2t=(1+x)/2，得证：

Γ(z)Γ(1/2)Γ(z+1/2)=22z−1Γ(z)Γ(z)Γ(z)\frac{\Gamma(z)\Gamma(1/2)}{\Gamma(z+1/2)}=2^{2z-1}\frac{\Gamma(z)\Gamma(z)}{\Gamma(z)}

Psi 函数

/Definition/

ψ\psi 函数是 Γ\Gamma 函数的对数微商：

ψ(z)=dln⁡Γ(z)dz=Γ′(z)Γ(z)\psi(z)=\frac{\text{d}\ln \Gamma(z)}{\text{d}z}=\frac{\Gamma'(z)}{\Gamma(z)}

性质：

(1) z=0,−1,−2,⋯z=0,-1,-2,\cdots 为函数的一阶极点，留数全部是 −1-1；除此之外函数全平面解析.

(2) 如下递推式：

ψ(z+1)=ψ(z)+1zψ(z+n)=ψ(z)+1z+1z+1+⋯+1z+n−1\psi(z+1)=\psi(z)+\frac{1}{z}\\ \psi(z+n)=\psi(z)+\frac{1}{z}+\frac{1}{z+1}+\cdots+\frac{1}{z+n-1}

(3)

ψ(1−z)=ψ(z)+πcot⁡πz\psi(1-z)=\psi(z)+\pi\cot\pi z

(4)

lim⁡n→∞[ψ(z+n)−ln⁡n]=0\lim_{n\to\infty}[\psi(z+n)-\ln n]=0

(5)

ψ(1)=−γ=−0.57721566⋯\psi(1)=-\gamma=-0.57721566\cdots

(6)

ψ(z)=−γ−1z+∑k=1∞(1k−1k+z)\psi(z)=-\gamma-\frac{1}{z}+\sum_{k=1}^\infty\left(\frac{1}{k}-\frac{1}{k+z}\right)

警告

考试考到 ψ\psi 函数，但是不要求记住这些结论，考试一般考证明 ψ\psi 函数的这些性质，也就是考利用 Γ\Gamma 函数进行计算.

接下来我们讲一些有意思的.

Riemann Zeta 函数

/Definition/

ζ(s)=∑n=1∞1ns\zeta(s)=\sum_{n=1}^\infty\frac{1}{n^s}

要求 ℜ(s)=σ>1\Re(s)=\sigma>1.

这个函数揭开了解析数论的序幕，之后就是代数几何了.

推广的版本是

ζ(s,a)=∑n=0∞1(n+a)s\zeta(s,a)=\sum_{n=0}^\infty\frac{1}{(n+a)^s}

由于

(n+a)−sΓ(s)=∫0∞xs−1e−(n+a)xdx(n+a)^{-s}\Gamma(s)=\int_0^\infty x^{s-1}e^{-(n+a)x}\text{d}x

可以得到 ζ(s,a)\zeta(s,a) 的解析延拓：

ζ(s,a)=−Γ(1−s)2πi∫∞(0+)(−z)s−1e−az1−e−zdz\zeta(s,a)=-\frac{\Gamma(1-s)}{2\pi\text{i}}\int_\infty^{(0+)}\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}\text{d}z

其中 ∣arg⁡(−z)<π∣|\arg(-z)<\pi|，围道内不含奇点 z=2nπiz=2n\pi\text{i} (n∈Zn\in\mathbb{Z}).

这个积分：

  • 对 ss 单值解析，所以是一个解析延拓，ℜ(s)>1\Re(s)>1 不再要求. 同时 aa 可以是复数，只要 ℜ(a)>0\Re(a)>0.
  • ζ(s,a)\zeta(s,a) 的奇点就是 Γ(1−s)\Gamma(1-s) 的奇点，所以只有一个，就是 s=1s=1，是一阶极点.

s=1s=1 处，留数是 11.

Hurwitz 证明了下述关系：

ζ(1−s)=2(2π)−sΓ(s)cos⁡sπ2ζ(s)\zeta(1-s)=2(2\pi)^{-s}\Gamma(s)\cos\frac{s\pi}{2}\zeta(s)

所以所有的 ζ(−2m)\zeta(-2m) (m∈Z+m\in\mathbb{Z}_+) 等于零. (？？)

得到：

1+1+⋯+1+⋯=−121+2+⋯+n+⋯=−11212+22+⋯+n2+⋯=013+23+⋯+n3+⋯=1120⋮\begin{aligned} &1+1+\cdots+1+\cdots=-\frac{1}{2}\\\\ &1+2+\cdots+n+\cdots=-\frac{1}{12}\\\\ &1^2+2^2+\cdots+n^2+\cdots=0\\\\ &1^3+2^3+\cdots+n^3+\cdots=\frac{1}{120}\\\\ &\quad\quad\quad\quad\quad\quad\vdots \end{aligned}

/Example/ (Casimir 效应)

真空的基态能量是一个每一个频率的谐振子基态不为零的那一个能量求和：

⟨E⟩=12∑ωℏω\braket{E}=\frac{1}{2}\sum_\omega\hbar\omega

如果在全空间求和，这是无意义的，因为真空的能量是多少都没有意义.

但是如果用两个板限制这个真空，频率会受到两板的限制，求和会得到：

⟨E⟩=hc4L∑n=1∞n\braket{E}=\frac{hc}{4L}\sum_{n=1}^\infty n

求和发散，但是如果用延拓的 ζ\zeta 函数，会得到

⟨E⟩=−hc48L\braket{E}=-\frac{hc}{48L}

当作一个势能，会有吸引力，当然这些现象在实验中还没有确切地观测到，但是至少 LIGO 做双镜修正的时候似乎考虑了这一点.

实际上，在理论物理中我们的计算是求和 ∑ne−εn\sum ne^{-\varepsilon n} (ε→0\varepsilon\to0). 这个求和类似配分函数，是一个对 ε\varepsilon 的求导.

当然求和的极限还是发散的，但是可以 Laurent 展开，第一项依赖于 1/ε1/\varepsilon，我们认为这是一个紫外发散，来自于我们计算方法的失误，鉴于板内外全部都有这一项，所以直接取第二项 −1/12-1/12 (常数项)，结果一致.

Riemann ζ\zeta 函数同时也和素数有关：

∏p(1−1ps)=1ζ(s)\prod_p\left(1-\frac{1}{p^s}\right)=\frac{1}{\zeta(s)}

其中，pp 是素数.

由此容易知道，ζ(s)\zeta(s) 在 σ=ℜ(s)>1\sigma=\Re(s)>1 的区域没有零点，前面已经证明 s=−2ms=-2m (m=1,2,⋯m=1,2,\cdots) 为 ζ(s)\zeta(s) 的零点，另外可以证明 σ<0\sigma<0 时，除了 s=−2ms=-2m 无零点.

其他零点只可能出现在 0≤σ≤10\leq\sigma\leq1 的区域内，Riemann 提出的猜想就是：

提示

这些零点都在 σ=1/2\sigma=1/2 的线上. —— Riemann 猜想

考试说明

30 分多值函数和级数相关 + 30 分留数定理相关 + Riemann 积分相关的部分 + Γ\Gamma 函数相关.

祝大家期末顺利.

更新日志

2025/10/9 02:50
查看所有更新日志
  • f85b5-build(theme): update theme to rc-168于
  • e5f81-feat(note): add complex note lesson-14于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)