外观
Lesson 13 辐角原理 & Γ 函数
约 2589 字大约 9 分钟
2025-6-3
留数定理 - 杂例
/Example/
Kepler 问题中的行星轨道:
dtdr=2E+r2k−r2l2
其中,E<0 为总机械能. 求行星运动周期.
在 Newton 力学中我们会配方,得到一个反三角函数;分析力学中则会代入轨道方程进行求解. 这里给出复变积分的方法:
T=∫2E+r2k−r2l2dr
在复变积分中,很有意思的是积分本身就沿着割线 (近日点 - 远日点连线),而且是顺时针的积分. 进一步处理:
2E+r2k−r2l2=r22E(r−rmin)(r−rmax)
其中,轨道半长轴满足 rmin+rmax=2a=−k/E.
为积分,只需要计算 ∞ 的留数. 先讨论 ∞ 的辐角:割线上岸为 0,∞ 处路径绕着远日点转了 −π,所以 arg∞=−π. 于是这一点为:
−2Ei⋅(1−rrmax)(1−rrmin)1=−2Ei[1+21(rmax+rmin)⋅r1+⋯]
所以留数是:
−2Ei⋅Ek⋅21
得到结果.
/Example/
计算积分:
∮∣z∣=2(z+3)(z5−1)dz
这个积分如果算 ∣z∣=2 内部的积分,要算 5 个奇点的留数;但是如果把圆外视作 “内部”,则:
- 围道方向相反;
- 无穷远点是特殊点;
- 只需要计算 z=3 和 z=∞ 两点的留数.
/Example/
计算积分:
∫−∞∞1+exeaxdx,0<a<1
半圆形围道不好,取高为 yi=2πi、宽为 2R 的矩形围道:
∮Cf(z)dz=∫−RR1+exeaxdx−∫−RR1+exe2aπieaxdx+∫02π1+eR+yiieaR+ayidy−∫02π1+e−R+yiie−aR+ayidy=(1−e2aπi)∫−RR1+exeaxdx
这里,竖直边的两个积分之和恰好为零,所以得到结果:
∫−∞∞1+exeaxdx=1−e2aπi−2πieaπi=sinπaπ
/Remark/
实际上,做换元 ex=t,上述积分就能化为根式函数的积分,积分围道也会变化为根式函数的积分围道.
此类积分在统计物理中常用.
/Example/
计算 Fermi 电子气模型的常用积分:
I=∫−∞∞(ex+1)2x2exdx
如果做变换 ex=t,被积函数中会出现 lnt,所以我们积分原来的积分时,要将被积函数改成:
w(z)=(ez+1)2z3ez
仿照上例的围道来求解.
/Example/
一个有趣的积分:
∮∣z∣=(m+1/2)πm∈Z,m→∞zntanzdz,n≥2,n∈Z
根据大圆弧引理,围道积分为零. 但是这样会导致我们得到一个求和:
0=k∈Z∑Reszntanz1z=kπ
而 k=0 时,所有极点都是一阶极点,可以计算出
Reszntanz1z=kπ,k=0=(kπ)n1
所以
k=1∑∞(kπ)n1((−1)n+1)=−Reszntanz1k=0
当 n 为偶数,就可以得到重要的求和式.
/Example/
证明固体物理中的如下等式:
k=0∑n−1sin2(2n2k+1π)1=n2
构造函数:
w(z)=(z−1)21zn+11
zw(z)→0 when z→∞,大圆弧引理得到围道积分为零. 所以留数和为零.
围道内有二阶极点 z=1 和 n 个一阶极点 zk=ei(2k+1)π/n.
Res[w(z)]∣z=1Res[w(z)]∣z=zk=dzdzn+11z=1=−4n=−n(zk−1)2zk=4nsin2(2n2k+1π)1
简单整理即证.
/Example/
计算积分:
∫−π/2π/21+εsinθcos2nθdθ,∣ε∣<1
当然可以用三角函数有理式积分方法,但是可以变成根式情形:
sinθ=x⟹∫−111+εx(1−x2)(2n−1)/2dx
/Example/
著名的 Gauss 积分:
∫−∞∞e−x2dx
提示
这个积分并不要求掌握,毕竟太难以想到.
我们已经知道积分会产生一个 π,但是复变积分难以得到这一类系数,所以我们考虑这样的构造:
∮Cf(z)dz=∮Ce2πz+1eiπz2+2πzdz
围道是如下非常恐怖的形式:
可以得到结果.
辐角原理
这是留数定理和 topology 结合的重要部分.
/Corollary/ (解析函数在零点和极点的对数留数)
设 z=a 为解析函数 w(z) 的 m 阶零点,则 z=a 为函数 w′(z)/w(z) 的一阶极点,且
Resw(z)w′(z)z=a=m
设 z=b 为解析函数 w(z) 的 n 阶极点,则 z=b 为函数 w′(z)/w(z) 的一阶极点,且
Resw(z)w′(z)z=b=−n
此引理证明不难. 由这一引理,立即得到所谓辐角原理:
/Theorem/ (辐角原理)
如果 w(z) 满足:
- 在简单闭合曲线 C 内除极点外解析;
- 在 C 上解析且不为零.
则:
2πi1∮Cw(z)w′(z)dz=N(w,C)−P(w,C)
其中 N 和 P 分别表示 w(z) 在 C 内零点与极点的个数 (一个 m 阶零点算 m 个;一个 n 阶极点算 n 个).
定理也可以用辐角来表达:
N(w,C)−P(w,C)=2πΔCargw(z)
接下来可以得到:
/Theorem/ (Rouche 定理)
如果函数 w(z) 和 φ(z) 在简单闭合曲线 C 内以及 C 上解析,且在 C 上恒满足 ∣w(z)∣>∣φ(z)∣,则函数 w(z) 与 w(z)+φ(z) 在 C 内部有同样多的零点 (几阶算几个).
/Proof/
引入辅助函数 ψ(z)=1+φ(z)/w(z).
可以有辐角原理知:
2πi1∮Cψψ′dz=0
得证.
Rouche 定理可以用来判断多项式根的分布,多项式在任意半径 R 圆内根的分布,相当于系数 akRn−k 多项式在单位圆内的情形.
R→∞ 可以证明代数学基本定理.
/Theorem/ (Weierstrass 定理)
设整函数 (复平面上无奇点) f(z) 只有不为零的一阶零点 a1,⋯,an,且 n→∞liman=∞.
且存在围道序列 {Cm} (围道内包含 m 个零点 a1∼am),在其上满足 ∣f′(z)/f(z)∣<M,M 为与 m 无关的正数,则 f(z) 可以展为无穷乘积:
f(z)=f(0)ef(0)f′(0)zn=1∏∞{(1−anz)ez/an}
/Proof/
关键在于证明:
F(z)=f(z)f′(z)=f(0)f′(0)+n=1∑∞{z−an1+an1}
只需要考虑围道积分:
2πi1∮Cζ(ζ−z)F(ζ)dζ
上述定理可以得到很多重要的无穷乘积,比如:
zsinz=n=1∏∞(1−n2π2z2)
Gamma 函数
/Definition/
最常用定义是:
Γ(z)=∫0∞tz−1e−tdt,ℜ(z)>0
这个积分称为第二类 Euler 积分,其中的变量 t 理解为 argt=0.
很多积分都能化为 Γ 函数,比如:
∫0∞e−t2tpdt=Γ(2p+1)/2
(Maxwell 速率分布率,极为常用)
下面要证明:积分在右半平面表示一个解析函数.
/Proof/
是瑕积分 (t=0 端),又是无穷积分,拆成两部分讨论:
∫0∞tz−1e−tdz=∫01tz−1e−tdz+∫1∞tz−1e−tdz
(1) t>1 时,被积函数全平面解析,只需要证明积分一致收敛.
我们知道
et=n=0∑∞n!tn
所以对于任意正整数 N,有
e−t<tNN!
这样似乎并不能得到证明,于是我们强行取一个内闭区域,得到:只要选择足够大的 N,积分就收敛.
(2) t<1 时,也还是证明积分收敛,考虑到:
∣e−ttz−1∣≤tδ−1
后者收敛.
综上所述,得证.
积分路径修改
在上面的积分定义中,我们可以发现改变 t 的积分路径,函数值不会变化:取一条不平行于虚轴的射线,积分值不变.
原理是:如下围道的大圆弧和小圆弧积分均是 0,但是大圆弧为零的条件是 e−t 在 ∞ 收敛,所以射线不能平行于虚轴.
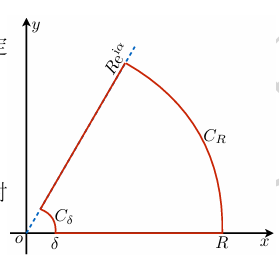
这并不是一种变量代换,而纯粹是积分路径的改变.
进一步,积分路径 L 可以是 t 平面上从 t=0 出发的任意分段光滑曲线,只需要最后以 ℜ(t)→+∞ 的方式趋于 ∞ 点即可.
解析延拓
我们想要把 Γ 函数延拓到左半平面. 所以我们要做一件非常流氓的方式 —— 交换求和和积分的次序.
将指数函数做 Taylor 展开,得到
∫01tz−1e−tdt=n=0∑∞n!(−)n∫01tn+z−1dt=n=0∑∞n!(−)nn+z1
奇点为 −n (n∈Z+),全部是一阶极点. 全平面版本的 Γ 函数是
Γ(z)=∫1∞tz−1e−tdt+n=0∑∞n!(−)nn+z1
留数是:
Res[Γ(z)]∣z=−n=n!(−1)n
所以奇点留数之和实际上就是 e−1,非常巧妙.
更新日志
2025/10/9 02:50
查看所有更新日志
f85b5-build(theme): update theme to rc-168于20ab5-fix(knowledge): mistake in complex lesson-13于9aea9-fix(display): change title于14e84-feat(note): add complex note于