Lesson 12 留数定理的应用 (2)

约 1872 字大约 6 分钟

2025-5-29

多值函数的积分

实变积分中不会出现多值，我们只有在将实变积分 ( $\arg z=0$ ) 变为复变积分的时候造成的一些多值性.

(1) 一种常见的多值函数积分：

I=\int_0^\infty x^{s-1}Q(x)\text{d}x

其中 $Q(x)$ 单值 (其实整体就是单值的，毕竟是实变积分，但是变为复变之后 $Q(x)$ 仍然单值).

为了保证积分是收敛的，有一个条件：

\lim_{x\to\infty}x^sQ(x)=0

对于相应的复变积分，积分围道应该要沿着割线 (正实轴) (不沿着割线就没办法做，因为只有这样积分围道内部才没有非孤立的奇点).

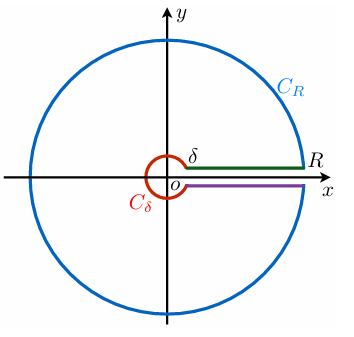
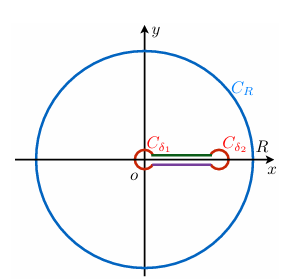
如图取围道，注意割线上下岸的积分变量分别是 $x$ 和 $xe^{2\pi\text{i}}$ ，积分被拆分为

\begin{aligned} \oint_Cz^{s-1}Q(z)\text{d}z&=\int_\delta^Rx^{s-1}Q(x)\text{d}x+\int_{C_R}z^{s-1}Q(z)\text{d}z\\\\ &\quad+\int_R^\delta(xe^{2\pi\text{i}})^{s-1}Q(x)\text{d}x+\int_{C_\delta}z^{s-1}Q(z)\text{d}z\\\\ &=\int_\delta^Rx^{s-1}Q(x)\text{d}x+\int_R^\delta(xe^{2\pi\text{i}})^{s-1}Q(x)\text{d}x \end{aligned}

如果 $s\in\mathbb{Z}$ 怎么办？

这个时候留数和也一定是零，之后再对 $s$ 求 L'Hopital 法则即可.
这种方法是一种比较笨的求 $0\to\infty$ 的、积不出来的积分的方法.

一般情况下，有

\begin{aligned} \int_0^\infty x^{s-1}Q(x)\text{d}x&=\frac{2\pi\text{i}}{1-e^{2\pi\text{i}s}}\sum\text{Res}\{z^{s-1}Q(z)\}\\\\ &=-\frac{\pi e^{-\pi\text{i}s}}{\sin(\pi s)}\sum\text{Res}\{z^{s-1}Q(z)\} \end{aligned}

如果 $Q(x)$ 具有一些对称性，则取割线的时候可以做得比较奇怪，比如将一个扇形作为割线 (割线的宽度并没有规定！)

/Example/

计算积分：
$\int_0^\infty\frac{x^{\alpha-1}}{x+e^{\text{i}\varphi}}\text{d}x\,,\quad0<\alpha<1\,,\quad-\pi<\varphi<\pi$
直接使用上面的结论，得到
$\int_0^\infty\frac{x^{\alpha-1}}{x+e^{\text{i}\varphi}}\text{d}x=\frac{\pi}{\sin\pi\alpha}\cdot e^{\text{i}\varphi(\alpha-1)}$
作为积分的一个特殊结果，取 $\varphi=0$ ，有
$\int_0^\infty\frac{x^{\alpha-1}}{x+1}\text{d}x=\frac{\pi}{\sin\pi\alpha}$
如果两边同时取虚部：
$\int_0^\infty\frac{x^{\alpha-1}}{x^2+2x\cos\varphi+1}\text{d}x=\frac{\pi}{\sin\pi\alpha}\frac{\sin(1-\alpha)\varphi}{\sin\varphi}$
这个积分可以在更大的范围成立，有 $0<\alpha<2$ .

/Example/

计算积分主值：
$\text{v.p.}\int_0^\infty\frac{x^{\alpha-1}}{x^2-1}\text{d}x\,,\quad0<\alpha<2$
取和上面相似的围道，但是在 $z=1$ 处是小圆弧引理；同时，上下半圆的积分是不连续的：
$\begin{aligned} \int_{C_{\delta\uparrow}}\frac{z^{\alpha-1}}{z^2-1}\text{d}z&=\lim_{z\to1}(z-1)\cdot\frac{z^{\alpha-1}}{z^2-1}\cdot\text{i}\Delta\arg=-\frac{\pi\text{i}}{2}\\\\ \int_{C_{\delta\downarrow}}\frac{z^{\alpha-1}}{z^2-1}\text{d}z&=\lim_{z\to1}(z-1)\cdot\frac{z^{\alpha-1}}{z^2-1}\cdot\text{i}\Delta\arg=-\frac{\pi\text{i}e^{2\pi\text{i}\alpha}}{2} \end{aligned}$
围道里面还剩下 $z=-1$ 一个奇点，留数值为 $e^{\text{i}\pi\alpha}/2$ . 所以积分主值为
$\text{v.p.}\int_0^\infty\frac{x^{\alpha-1}}{x^2-1}\text{d}x=\frac{\pi\text{i}}{2}\frac{(1+e^{\text{i}\alpha\pi})^2}{1-e^{2\text{i}\alpha\pi}}=-\frac{\pi}{2}\cot\frac{\pi}{2}$
考虑到 $x<1$ 时的贡献最大，这个负号是合理的.

/Example/

计算积分：
$\int_0^\infty\frac{1}{1+x+x^2}\text{d}x$
其实可以用配方的方法积出 $\arctan$ 函数.
在复变函数的领域，我们引入根式因子的办法来求解：
$\int_0^\infty\frac{x^{\alpha-1}}{1+x+x^2}\text{d}x$
实际上此题难点完全来自于留数的计算困难.
奇点是 $z=e^{2\pi\text{i}/3}$ 和 $z=e^{4\pi\text{i}/3}$ ，这两个都是一阶极点，得到
$\sum\text{Res}=\frac{(e^{2\pi\text{i}/3}-1)e^{2\pi\alpha\text{i}/3}+(e^{4\pi\text{i}/3}-1)e^{4\pi\alpha\text{i}/3}}{3}$
(这实在是太… 为什么不配方呢？) 总之答案是
$\int_0^\infty\frac{1}{1+x+x^2}\text{d}x=\frac{2\sqrt{3}\pi}{9}$

(2) 另一种常见的多值函数积分 (涉及到对数函数)：

/Example/

计算积分：
$\int_0^\infty\frac{\ln x}{1+x+x^2}\text{d}x$
取类似的围道，计算复变积分：
$\begin{aligned} \oint_C\frac{\ln z}{1+z+z^2}\text{d}z&=\int_\delta^R\frac{\ln x}{1+x+x^2}\text{d}x+\int_{C_R}\frac{\ln z}{1+z+z^2}\text{d}z\\\\ &\quad+\int_R^\delta\frac{\ln (xe^{2\pi\text{i}})}{1+x+x^2}\text{d}x+\int_{C_\delta}\frac{\ln z}{1+z+z^2}\text{d}z\\\\ &=2\pi\text{i}\sum\text{Res}\left\{\frac{\ln z}{1+z+z^2}\right\}\\\\ &=2\pi\text{i}\left(\frac{2\pi}{3\sqrt3}-\frac{4\pi}{3\sqrt3}\right)=-\frac{4\pi^2\text{i}}{3\sqrt3} \end{aligned}$
大小圆弧引理给出两个圆上的积分是 $0$ ，结果我们得到的是积分：
$\int_0^\infty\frac{\ln x}{1+x+x^2}\text{d}x-\int_0^\infty\frac{\ln x+2\pi\text{i}}{1+x+x^2}\text{d}x=-\frac{4\pi^2\text{i}}{3\sqrt3}$
反而计算出了我们之前想要的积分. 但是现在我们目前的积分怎么办？
我们失败的原因是，乘上了一个对数，导致少了一个对数. 所以为什么不再乘一个对数？
计算积分：
$\begin{aligned} &\int_0^\infty\frac{\ln^2x}{1+x+x^2}\text{d}x-\int_0^\infty\frac{(\ln x+2\pi\text{i})^2}{1+x+x^2}\text{d}x\\\\ &=2\pi\text{i}\sum\text{Res}\left\{\frac{\ln^2z}{1+z+z^2}\right\}\\\\ &=\frac{2\pi}{\sqrt{3}}\left[\frac{16}{9}\pi^2-\frac{4}{9}\pi^2\right]=\frac{8\sqrt{3}}{9}\pi^3 \end{aligned}$
有
$-4\pi\text{i}\int_0^\infty\frac{\ln x}{1+x+x^2}\text{d}x+4\pi^2\int_0^\infty\frac{1}{1+x+x^2}\text{d}x=\frac{8\sqrt3}{9}\pi^3$
发现实部和虚部是分开的，得到原来我们要求的积分：
$\int_0^\infty\frac{\ln x}{1+x+x^2}\text{d}x=0$
(如果一个积分是 $0$ ，肯定有额外的对称性，简单的验证是换元 $t=\ln x$ ，发现为奇函数.)

杂例

/Example/

计算定积分：
$\int_0^1\frac{x^{1-p}(1-x)^p}{1+x}\text{d}x\,,\quad -1<p<2$
在 $0$ 和 $1$ 两个点处围小圈，外面再套一个大圆弧.
沿着小圆弧的积分均为 $0$ . 注意到，留数为
$\text{Res}f(-1)=-2^pe^{-p\pi\text{i}}$
割线下岸的函数值为
$f(z)=\frac{x^{1-p}(1-x)^pe^{-2p\pi\text{i}}}{1+x}$
但是大圆弧引理已经不成立，因为 $\infty$ 的函数值 $f(\infty)=e^{-p\pi\text{i}}$ 而不是 $0$ . 不过我们很早就知道， $\infty$ 为场点时，可以直接使用 Laurent 展开计算其留数，那么我们有：
$f(z)=e^{-p\pi\text{i}}\left[1-(p+1)\frac{1}{z}+\frac{p(p+1)}{2}\frac{1}{z^2}-\cdots\right]$
但是 $\infty$ 点的留数要加一个 " $-$ " 号，因为积分是顺时针的. 所以有
$\text{Res}f(\infty)=(1+p)e^{-p\pi\text{i}}$
代回，原积分为
$\int_0^1\frac{x^{1-p}(1-x)^p}{1+x}\text{d}x=\frac{\pi(1+p-2^p)}{\sin p\pi}$
当然，也可以换元，把 $0\to1$ 的积分换成 $0\to\infty$ 上的，变为我们熟悉的问题.