菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 11 留数定理的应用 (1)

复制页面

约 2378 字大约 8 分钟

2025-5-27

留数定理

/Example/

计算积分

I=∫0∞dx1+x4I=\int_0^\infty\frac{\text{d}x}{1+x^4}

用正虚轴来计算，画 1/41/4 圆作为围道. 那么奇点只有一个：z=eiπ/4z=e^{\text{i}\pi/4}. 所以

I+I′+ICR=(1−eiπ/2)I=(11+z4)′∣z=eiπ/4I+I'+I_{C_R}=(1-e^{\text{i}\pi/2})I=\left.\left(\frac{1}{1+z^4}\right)'\right|_{z=e^{\text{i}\pi/4}}

得到积分值：

∫0∞dx1+x4=24π\int_{0}^\infty\frac{\text{d}x}{1+x^4}=\frac{\sqrt2}{4}\pi

/Remark/

如果 xx 沿着某条线不变，就可以取扇形的围道，只要情况满足 f(z)=f(zeiθ)f(z)=f(ze^{\text{i}\theta})，就可以分成扇形的围道. 注意，弧上的积分值仍然为零，但是半径方向的积分可以提出公因子，而且扇形内部只有一个奇点.

拓展的一个例子：

/Example/

计算积分：

∫0∞dx1+x3\int_0^\infty\frac{\text{d}x}{1+x^3}

考虑 2π/32\pi/3 的围道：

∮Cdz1+z3=∫0Rdx1+x3+∫CRdz1+z3+∫R0e2iπ/3dx1+x3=(1−e2iπ/3)∫0Rdx1+x3\begin{aligned} \oint_C\frac{\text{d}z}{1+z^3}&=\int_0^R\frac{\text{d}x}{1+x^3}+\int_{C_R}\frac{\text{d}z}{1+z^3}+\int_R^0\frac{e^{2\text{i}\pi/3}\text{d}x}{1+x^3}\\ &=(1-e^{2\text{i}\pi/3})\int_0^R\frac{\text{d}x}{1+x^3} \end{aligned}

(极限 z→∞z\to\infty 时圆弧 CRC_R 上的积分为零)

这个东西等于留数和：

2πiRes(11+z3)∣z=eiπ/3=2π3e−iπ/62\pi\text{i}\text{Res}\left.\left(\frac{1}{1+z^3}\right)\right|_{z=e^{\text{i}\pi/3}}=\frac{2\pi}{3}e^{-\text{i}\pi/6}

得到结果：

∫0∞dx1+x3=2π33\int_0^\infty\frac{\text{d}x}{1+x^3}=\frac{2\pi}{3\sqrt3}

含三角函数的无穷积分

形如这样的积分：

I=∫−∞∞f(x)cos⁡pxdx ,I=∫−∞∞f(x)sin⁡pxdxI=\int_{-\infty}^\infty f(x)\cos px\text{d}x\,,\quad I=\int_{-\infty}^\infty f(x)\sin px\text{d}x

处理这种类型的积分，仍然可以采用半圆形围道，但是被积函数不能简单写成 f(z)cos⁡zf(z)\cos z 或者 f(z)sin⁡zf(z)\sin z，因为 cos⁡z\cos z 和 sin⁡z\sin z 沿着虚轴的行为是发散的，不能计算大圆弧积分.

注意

如果考试的时候直接不加思考地使用留数定理，完全不给分.

正确的做法是，将被积函数同一取为 f(z)eipzf(z)e^{\text{i}pz}，之后取实部就是 cos⁡z\cos z 的积分，取虚部是 sin⁡z\sin z 的积分.

但是能够变换则必须要求：f(x)f(x) 为实函数，且 pp 为实数. 不妨假设 pp 为正，如果为 "−-"，可以在变换的时候写 e−ipze^{-\text{i}pz}，取虚部的时候再加一个符号.

有：

∮Cf(z)eipzdz=2πi∑Res{f(z)eipz}\oint_Cf(z)e^{\text{i}pz}\text{d}z=2\pi\text{i}\sum\text{Res}\{f(z)e^{\text{i}pz}\}

下面证明大圆弧上的积分趋于零：

/Theorem/ (Jordan 引理)

设在 0≤arg⁡z≤π0\leq\arg z\leq\pi 的范围内，当 ∣z∣→∞|z|\to\infty 时，Q(z)Q(z) 一致地趋近于 00,则

lim⁡R→∞∫CRQ(z)eipzdz=0\lim_{R\to\infty}\int_{C_R}Q(z)e^{\text{i}pz}\text{d}z=0

其中 p>0p>0，CRC_R 是原点为圆心，RR 为半径的上半圆.

提示

这个 Jordan 就是量子力学的三位创始人之一. 但是当年他只是把 Heisenberg 丑陋的写法统一成了矩阵力学的标准形式而已. 所以有的时候科研并不能看到自己在做的事情的实际意义.

/Proof/

这个要求比普通的留数定理要低，所以放缩显得更加重要.

∣∫CRQ(z)eipzdz∣=∣∫0πQ(Reiθ)eipR(cos⁡θ+isin⁡θ)Reiθidθ∣≤∫0π∣Q(Reiθ)∣e−pRsin⁡θRdθ≤εR∫0πe−pRsin⁡θdθ=2εR∫0π/2e−pRsin⁡θdθ\begin{aligned} \left|\int_{C_R}Q(z)e^{\text{i}pz}\text{d}z\right|&=\left|\int_0^\pi Q(Re^{\text{i}\theta})e^{\text{i}pR(\cos\theta+\text{i}\sin\theta)}Re^{\text{i}\theta}\text{i}\text{d}\theta\right|\\ &\leq\int_0^\pi|Q(Re^{\text{i}\theta})|e^{-pR\sin\theta}R\text{d}\theta\\ &\leq\varepsilon R\int_0^\pi e^{-pR\sin\theta}\text{d}\theta\\ &=2\varepsilon R\int_0^{\pi/2}e^{-pR\sin\theta}\text{d}\theta \end{aligned}

现在我们要精确地估计 sin⁡θ\sin\theta 的值. 将 sin⁡θ\sin\theta 往更小的线性形式上变化，放缩为 sin⁡θ≥2θ/π\sin\theta\geq2\theta/\pi. 得到

∣∫CRQ(z)eipzdz∣<2εR∫0π/2e−pR⋅2θ/πdθ=2εR⋅π2pR(1−e−pR)=επp(1−e−pR)\begin{aligned} \left|\int_{C_R}Q(z)e^{\text{i}pz}\text{d}z\right|&<2\varepsilon R\int_0^{\pi/2}e^{-pR\cdot2\theta/\pi}\text{d}\theta\\ &=2\varepsilon R\cdot\frac{\pi}{2pR}(1-e^{-pR})\\ &=\frac{\varepsilon\pi}{p}(1-e^{-pR}) \end{aligned}

这就证明了大圆弧上的积分为零.

/Example/

计算积分：

I=∫0∞xsin⁡xx2+a2dx ,a>0I=\int_0^\infty\frac{x\sin x}{x^2+a^2}\text{d}x\,,\quad a>0

先要记得解析延拓到 −∞→∞-\infty\to\infty，这是第一步：熟知

I=12∫−∞∞xsin⁡xx2+a2dxI=\frac{1}{2}\int_{-\infty}^\infty\frac{x\sin x}{x^2+a^2}\text{d}x

化为复变积分，计算留数：

2πi⋅12ei⋅ia=iπe−a2\pi\text{i}\cdot\frac{1}{2}e^{\text{i}\cdot\text{i}a}=\text{i}\pi e^{-a}

提示

留数定理计算的大多数正常问题都是一阶极点，所以说大多数情况是很好计算的.

注意

一定要记得 2πi2\pi\text{i}！

所以取虚部得到积分为 I=(π/2)e−aI=(\pi/2)e^{-a}，同时可以得到实部为 00.

实轴上有奇点的情形

/Example/ (瑕积分)

∫abf(x)dx=lim⁡δ1→0∫ac−δ1f(x)dx+lim⁡δ2→0∫c+δ2bf(x)dx\int_a^bf(x)\text{d}x=\lim_{\delta_1\to0}\int_a^{c-\delta_1}f(x)\text{d}x+\lim_{\delta_2\to0}\int_{c+\delta_2}^bf(x)\text{d}x

若极限单独不存在，但是

lim⁡δ→0[∫ac−δf(x)dx+∫c+δbf(x)dx]\lim_{\delta\to0}\left[\int_a^{c-\delta}f(x)\text{d}x+\int_{c+\delta}^bf(x)\text{d}x\right]

存在，则称为瑕积分的主值存在，记为

v.p.∫abf(x)dx=lim⁡δ→0[∫ac−δf(x)dx+∫c+δbf(x)dx]\text{v.p.}\int_a^bf(x)\text{d}x=\lim_{\delta\to0}\left[\int_a^{c-\delta}f(x)\text{d}x+\int_{c+\delta}^bf(x)\text{d}x\right]

如果瑕积分及其主值都存在，那么它们一定相等.

/Example/

如下积分 (来自 PRB 的某一篇文献)：

∫−∞∞∫−∞∞y−b(x−a)2+(y−b)2dxdy\int_{-\infty}^\infty\int_{-\infty}^\infty\frac{y-b}{(x-a)^2+(y-b)^2}\text{d}x\text{d}y

既是反常积分，又是瑕积分.

而且因为是双重积分，所以区域是一个正方形，在奇点附近也要围出一个正方形.

/Example/

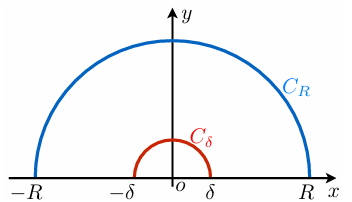
计算积分：

I=∫−∞∞dxx(1+x+x2)I=\int_{-\infty}^\infty\frac{\text{d}x}{x(1+x+x^2)}

反常积分，反常性既表现在积分区间为无穷区间，又表现为被积函数在 x=0x=0 点不连续 (x=0x=0 点为瑕点)，次积分在主值意义下存在.

取围道有两段圆弧 CRC_R 和 CδC_\delta，前者 R→∞R\to\infty，后者 δ→0\delta\to0. 如图

∮Cdzz(1+z+z2)=∫−R−δdxx(1+x+x2)+∫Cδdzz(1+z+z2)+∫δRdxx(1+x+x2)+∫CRdzz(1+z+z2)\begin{aligned} &\oint_C\frac{\text{d}z}{z(1+z+z^2)}\\ &=\int_{-R}^{-\delta}\frac{\text{d}x}{x(1+x+x^2)}+\int_{C_\delta}\frac{\text{d}z}{z(1+z+z^2)}\\ &\quad+\int_\delta^R\frac{\text{d}x}{x(1+x+x^2)}+\int_{C_R}\frac{\text{d}z}{z(1+z+z^2)} \end{aligned}

计算 CδC_\delta 的积分，用小圆弧引理，注意到是顺时针旋转，所以积分值的极限为 −iπ-\text{i}\pi.

/Remark/

这里的条件是要求一致收敛，小圆弧才有极限. 所以奇点至多是一阶极点，阶数比一阶小也可以 (比如 1/21/2 阶).

计算留数：

2πiRes1z(1+z+z2)∣z=e2πi/3=−π3−πi2\pi\text{i}\text{Res}\left.\frac{1}{z(1+z+z^2)}\right|_{z=e^{2\pi\text{i}/3}}=-\frac{\pi}{\sqrt3}-\pi\text{i}

(这里的计算技巧是取立方差公式，算倒函数零点) 最后计算出瑕积分主值为

v.p.∫−∞∞dxx(1+x+x2)=−π3\text{v.p.}\int_{-\infty}^\infty\frac{\text{d}x}{x(1+x+x^2)}=-\frac{\pi}{\sqrt3}

一些定性验证的方法：在负半轴分母小一点，所以结果应该是负的.

/Remark/

如果小圆弧 CδC_\delta 画在下半平面？

多一个奇点，这个奇点如果比一阶极点的阶数低，当然我们可以这么计算.

不过这样增加奇点个数肯定不是很好算.

/Example/

计算积分：

I=∫−∞∞sin⁡xxdxI=\int_{-\infty}^\infty\frac{\sin x}{x}\text{d}x

这个积分本身不是瑕积分，但是化为复变积分的时候产生了奇点.

实变函数上，我们做这个积分可以引入

I(t)=∫−∞∞e−xtsin⁡xxdxI(t)=\int_{-\infty}^\infty\frac{e^{-xt}\sin x}{x}\text{d}x

之后对 tt 求导，得到

I′(t)=∫−∞∞e−xtsin⁡xdxI'(t)=\int_{-\infty}^\infty e^{-xt}\sin x\text{d}x

可以分部积分，之后再对 tt 积分.

在复变函数上我们改写成：

∮Ceizzdz\oint_C\frac{e^{\text{i}z}}{z}\text{d}z

z=0z=0 变成了奇点. 还是按照上面的方法，积分得到为 π\pi.

用上面的方法，还可以算出：

∫−∞∞sin⁡2xx2dx=π ,∫−∞∞sin⁡3xx3dx=34π∫−∞∞sin⁡4xx4dx=23π ,∫−∞∞sin⁡5xx5dx=115192π\int_{-\infty}^\infty\frac{\sin^2x}{x^2}\text{d}x=\pi\,,\quad\int_{-\infty}^\infty\frac{\sin^3x}{x^3}\text{d}x=\frac{3}{4}\pi\\ \int_{-\infty}^\infty\frac{\sin^4x}{x^4}\text{d}x=\frac{2}{3}\pi\,,\quad\int_{-\infty}^\infty\frac{\sin^5x}{x^5}\text{d}x=\frac{115}{192}\pi

我们来计算 2,32,3 次的结果：

22 次的换法不同，用三角函数的定义

sin⁡2z=−e2iz+e−2iz−24\sin^2z=-\frac{e^{2\text{i}z}+e^{-2\text{i}z}-2}{4}

注意，我们只要实部，所以算这个也是一样的：

−e2iz−12-\frac{e^{2\text{i}z}-1}{2}

最后我们计算积分：

∮C1−e2iz2z2dz\oint_C\frac{1-e^{2\text{i}z}}{2z^2}\text{d}z

(z=0z=0 是一阶极点)

33 次的换法也不一样 (当然从 44 次开始就可以和前面类比了)，仍然用定义

i⋅e3iz−3eiz+3e−iz−e−3iz8z3\text{i}\cdot\frac{e^{3\text{i}z}-3e^{\text{i}z}+3e^{-\text{i}z}-e^{-3\text{i}z}}{8z^3}

这里我们要的是虚部 (因为前面有一个 i\text{i})，所以换成

2i⋅e3iz−3eiz8z32\text{i}\cdot\frac{e^{3\text{i}z}-3e^{\text{i}z}}{8z^3}

但是这不是一阶极点，所以我们在保证后面的一块分数虚部不变的情况下，加上一个实部：

2i⋅e3iz−3eiz+28z32\text{i}\cdot\frac{e^{3\text{i}z}-3e^{\text{i}z}+2}{8z^3}

之后做积分.

作业中也有一道类似这样的题目：

∫−∞∞x−sin⁡xx3dx\int_{-\infty}^\infty\frac{x-\sin x}{x^3}\text{d}x

如果正常变换，取下面积分的虚部：

∫−∞∞ix−eixx3dx\int_{-\infty}^\infty\frac{\text{i}x-e^{\text{i}x}}{x^3}\text{d}x

似乎是三阶极点，所以直接在分子上加上一个实部 11，做计算即可.

上述积分 (sin⁡x/x\sin x/x) 也可以利用之前的方法来去掉奇点：

∫−∞∞sin⁡xxdx=lim⁡ε→0xsin⁡xx2+ε2dx\int_{-\infty}^\infty\frac{\sin x}{x}\text{d}x=\lim_{\varepsilon\to0}\frac{x\sin x}{x^2+\varepsilon^2}\text{d}x

更新日志

2025/10/9 02:50
查看所有更新日志
  • f85b5-build(theme): update theme to rc-168于
  • 7ced5-feat(note): add complex note于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)