Lesson 14 Dynamics of biological networks (2)

约 855 字大约 3 分钟

2025-12-23

生物网络：

上面的这些内容整体上可以组成一个「图」，图中可以存在加权重的连接等等.

一维正反馈效应：

\frac{\text{d}[x]}{\text{d}t}=v\frac{[x]^n}{K_d^n+[x]^n} - d\cdot[x]

这个方程很明显难以得到解析的解，而且其解析解的实际意义也并不大. 事实上，我们更倾向于考虑分析这个方程的稳定性. 也就是对于 $\text{d}x^*/\text{d}t=f(x^*)$ 这样的情况，分析 $x = x^*+\delta x$ 造成的结果. 稳定态和不稳定态之间存在「分叉」.

提示

我认为，这里的一维方程分叉和理论力学混沌理论中的 Logistic 映射可能有类似的机制.

基因开关：考虑某个基因被抑制的概率为

p_b(c)=\frac{c^n}{c^n+K_d^n}

(仍然取一个 Hill 反应的形式.) 转录对应的方程为

\frac{\text{d}u}{\text{d}t} = -u+\frac{\alpha}{1+v^n},\quad\frac{\text{d}v}{\text{d}t}=-v+\frac{\alpha}{1+u^n}

一共有两个基因，这是无量纲化的方程. 我们期望先找到不动点，也就是系统长时演化之后的情况；之后在不动点附近展开.

u_0=\frac{\alpha}{1+v_0^n},\quad v_0=\frac{\alpha}{1+u_0^n}\Longrightarrow\frac{\text{d}}{\text{d}t}\begin{pmatrix} \delta u\\\delta v \end{pmatrix}=\begin{pmatrix} f_u&f_v\\g_u&g_v \end{pmatrix}\begin{pmatrix} \delta x\\\delta y \end{pmatrix}

这个系数矩阵 (Jacobi Matrix) 给出两个本征值，它们的正负表现了两个不动点的稳定性，可能出现鞍点、旋进或者旋出的不同情况.

对于一个非常复杂的大型生物网络，我们的处理哲学是「Less is More」，期望达到的效果是把不重要的成分全部丢掉. 操作中类似于统计方法中的 $k$ - NN，用周围的状态给这个网格节点投票，决定其下一个步骤的演化.

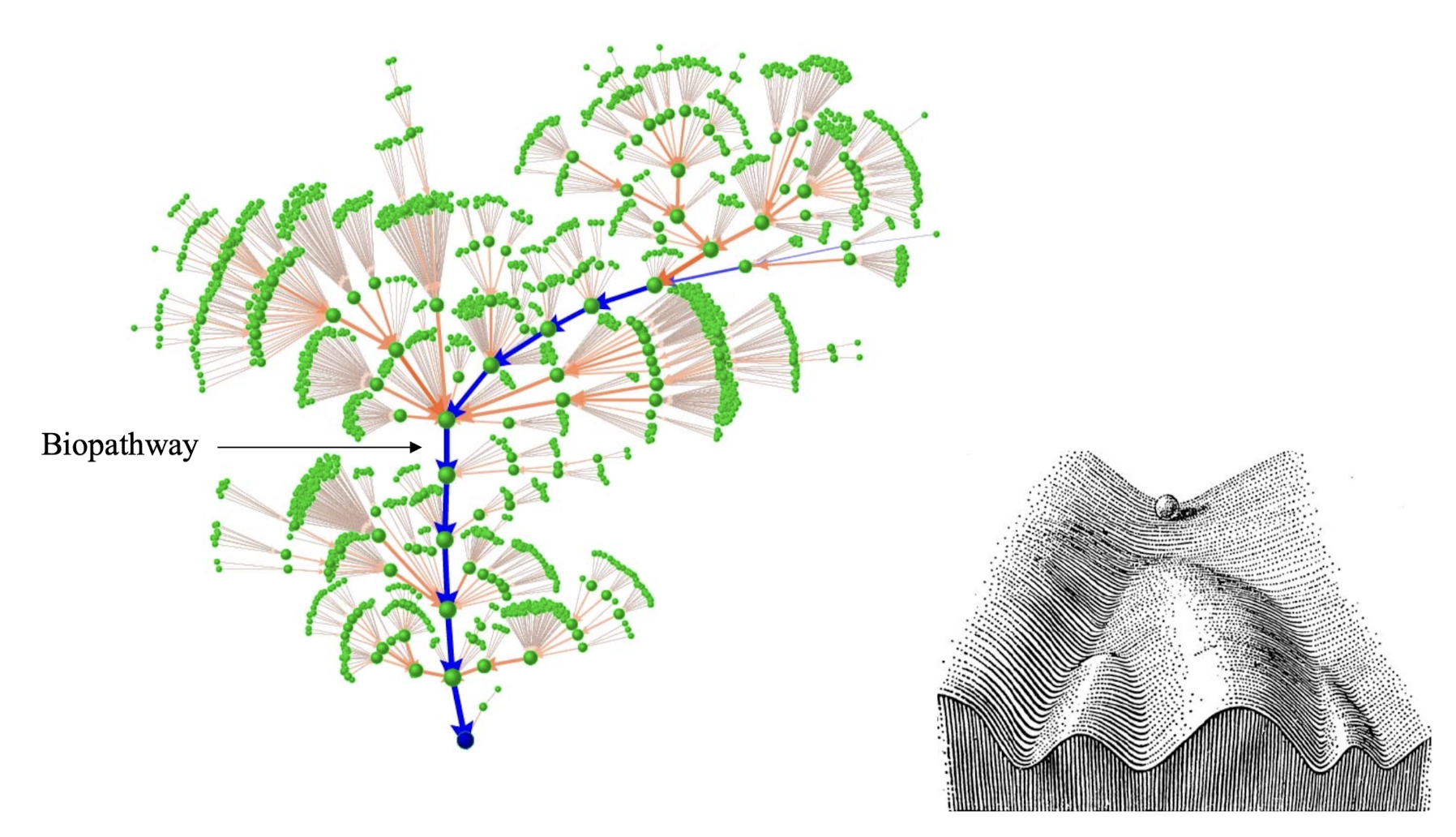
这样的主干道径迹就是一种所谓的吸引子，对于生物而言，甚至可以是一个吸引盆，生物网络的稳定性是非常好的. 这种稳健的特性本质上来源于网络自身的连接方式.

遗憾的是这样的理论取得的成果并不好... 因为我们并没有通过这个理论来解答很多实际问题，这是一个悲伤的故事；不过这样的事情也是常见的.

Hopfield Network & Spin-glass (自旋玻璃)：

注意

物理学家在做什么，什么就是物理.

Hopfield 一开始仅仅是组建了一个二十多人的 seminar 团队而已，研究有没有什么 toy model 能够解释「记忆是如何储存在神经网络中的」. 这里面有神经科学家、动物行为学家，还有凝聚态物理学家... 非常混乱的一个团队. 但是也在这种情况下诞生了 Nobel 级别的理论.

自旋玻璃在某种意义上和 Ising 模型是类似的.

本学期课程的最后一个板块 —— 自组织.

更新日志

2025/12/23 13:26

查看所有更新日志

版权归属：physnya