Lesson 12 absorbing

约 925 字大约 3 分钟

2025-12-09

有必要跟大家讲一讲 Maxwell's Demon. 实际上是在一个盒子里面放一块挡板，然后一个小妖精来控制这个挡板，当分子向这个挡板撞过来的时候，会推动挡板做功. 每做一次功，小妖就抽出挡板再重新放回去一次，使得挡板永远受到分子的碰撞做正功.

这样就实现了「从单一热源吸热做功，而不对外界造成任何影响.」问题出在「不对外界造成任何影响」上，小妖的记忆并没有在每一次操作之后回到初态.

吸收的不确定度：

\frac{\sigma_c^2}{\bar{c}^2}=\frac{1}{4\pi DacT}

细菌能够感知两个地方的浓度差异 $\Delta c$ ，作为一个信号. 但是要求信噪比大于 1 才能提取出信号，如果浓度梯度为 $g$ ，则要求

\Delta c=g\Delta l=gTv>\delta c\sim\sqrt{\frac{c}{4DsT}}

实际计算表明大约要 $0.5\text{ s}$ 才能够感知到浓度的变化. 结合我们上节课说的 E.coli 的 run and tumble，实验中测量它每次 run 的时间就是大概 $1\text{ s}$ ，这说明「感知浓度变化」是 run 这个时间的主要决定因素.

回到受体和配体的问题上来，膜上分布了大量的受体，有些结合了配体、有些没有结合，这个结合数的信息被记录为 $\phi$ ， $\phi=\phi(L)=\displaystyle{\frac{a(L)}{M}}$ ，之后在信息处理中枢里面的信号是 $R=f(\phi)$ .

最简单的机制是全部线性的：

R\sim \phi\sim\frac{L}{M}

但是如果是这样，膜上的 $10^{13}$ 个受体应该要有很大一部分结合，才能产生可观的信号，而且难以分辨变化. 所以我们需要放大机制：

a(L)\sim\frac{L^n}{K^n+L^n}

同时 $f(\phi)$ 是所谓 ultrasensitive 的放大函数，比如下面的 G 蛋白耦联机制：

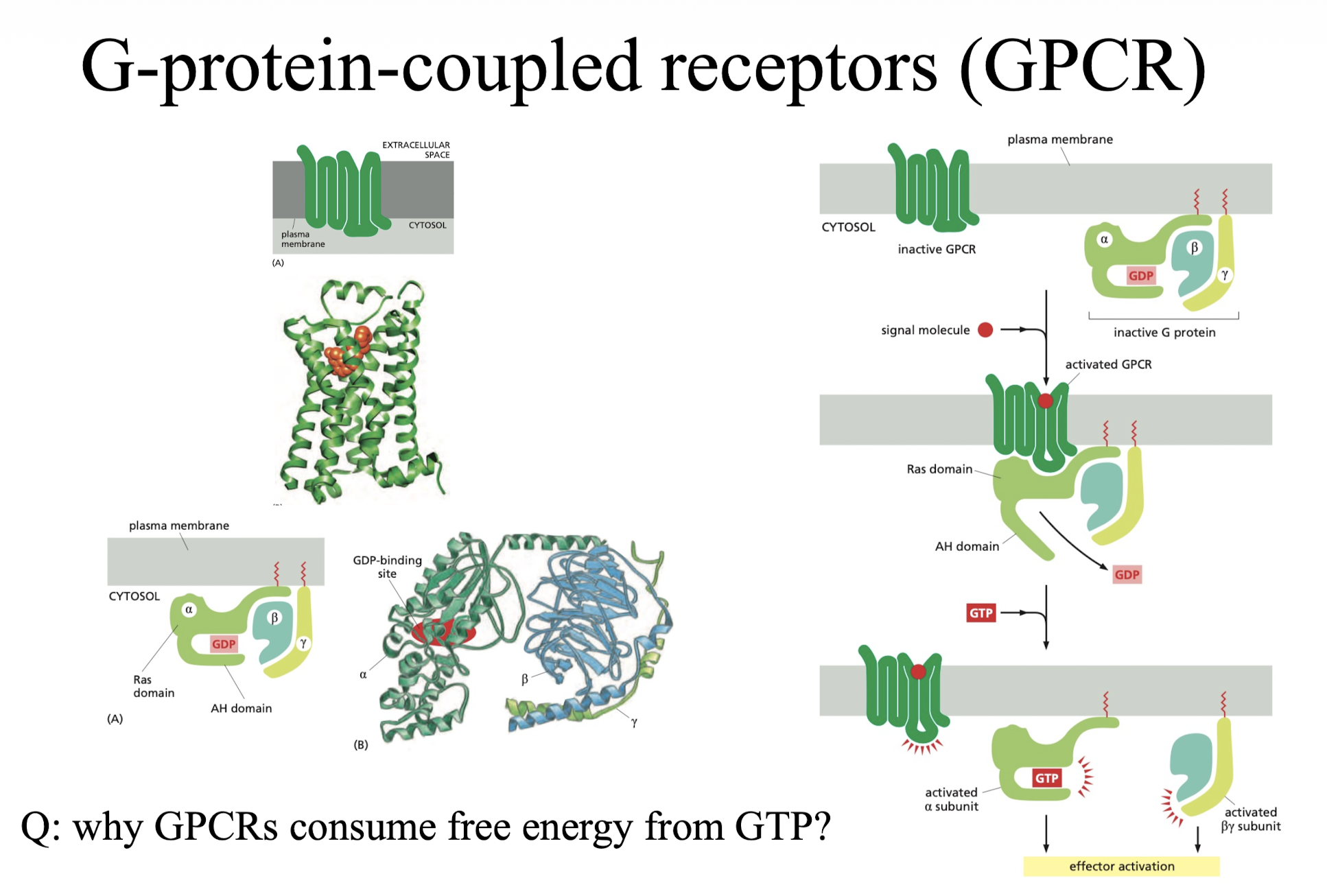
仍然回到我们之前多次讲的四态系统，这一次因为有 GTP 这种高能分子的存在，原来的细致平衡条件不再成立，有

\frac{k_+(\gamma\omega_+)ck_-(\gamma\omega_-)}{k_-\omega_+k_+\omega_-}=\gamma^2\neq1

激活状态和非激活状态的比例为

S([L]=0)=\frac{\omega_+}{\omega_++\gamma\omega_-},\quad S([L]=\infty)=\frac{\omega_+}{\omega_++\omega_-/\gamma}

对于 $\gamma\gg1$ 的情况 (驱动很强)，

S\approx\frac{[L]}{K_d+[L]}

产生一个 Hill 函数.

后面的放大由级联反应完成，就像光电倍增管一样，通过引入能量的方式不断指数放大信号：

两个酶反应：

\begin{aligned} &\text{E}+\text{K}\stackrel{q_1}{\underset{q_{-1}}{\rightleftharpoons}}\text{EK}\stackrel{q_2}{\underset{q_{-2}}{\rightleftharpoons}}\text{Ep}+\text{K}\\\\ &\text{Ep}+\text{P}\stackrel{q_3}{\underset{q_{-3}}{\rightleftharpoons}}\text{Ep}\cdot\text{P}\stackrel{q_4}{\underset{q_{-4}}{\rightleftharpoons}}\text{E}+\text{P} \end{aligned}

通过它们的稳态可以得到 ultrasensitive.

我们可以说，细致平衡阻碍了 Hill 系数的增大，也就拉低了超敏反应的敏感程度. 而维持非平衡态，就需要能量的输入. 所以又回到了我们提到的 Maxwell's Demon，这产生了「对外界的影响」.

下节课我们讲「适应」：我们知道 Hill 函数的图像是一个高速上升的曲线，但是这会导致这个反应只能测量一小段范围的浓度变化，一旦超出这个范围，系统就几乎没有响应. 所以需要平移这个曲线，在每一次测量之后调整基准值，这就是适应.

更新日志

2025/12/9 14:53

查看所有更新日志

版权归属：physnya