外观
Riemann 几何与张量分析
约 16440 字大约 55 分钟
2025-09-02
警告
本章内容很多,所以估计会多次更新.
如果你在文章中看到了这样 的符号,可以点击它,它是一个小小的注释,可能含有通往参考文献的链接.
2025/09/02 - 02:31,我已经更新完这篇笔记,为了重新提交一次 RSS 记录,我修改了 markdown 文件中自动生成的时间,从 2025/08/15 -14:09:31 改为 2025/09/02 - 02:36:17. 同时移除了 DRAFT 标记.
狭义相对论中的张量
狭义相对论研究四维 Minkowski 时空 (一种平直时空),在这样的时空中,用张量的语言表示 Lorentz 变换:
xμ′=aμαxα,μ,α=1,2,3,4;x4=ict
或写成:
dxμ′=aμαdxα
「线性」体现在变换矩阵元 aμα 不依赖于坐标. 上面的式子已经采用了 Einstein 求和惯例.
光速不变原理要求,时空间隔在 Lorentz 变换下保持不变:
ds2=dxμ′dxμ′=dxαdxα
因此变换矩阵一定是正交矩阵,满足 a~=a−1. (a 的转置矩阵记为 a~).
张量的定义有两个要点:分量个数 & 在坐标变化下按照特定的规律变换.
狭义相对论中:
零阶张量 (标量) 定义为 Lorentz 变换下的不变量,
U′(x′)=U(x)
(这里
\bold表示数组 xμ(′),μ=1,2,3,4). 标量只有一个分量.一阶张量 (矢量) 定义为由四个分量组成的一个量,它在 Lorentz 变换下像坐标微分一样变换:
Vμ′=aμαVα,μ,α=1,2,3,4
二阶张量用下式定义:
Tμν′=aμαaνβTαβ
n 阶张量的变换方式是:
Tμν⋯λ′=aμαaνβ⋯aλσTαβ⋯σ
几个具体的张量和 Lorentz 变换的形式:
(1) Lorentz 变换:
dx1′dx2′dx3′dx4′=γ00−iβγ01000010iβγ00γdx1dx2dx3dx4
(2) 电磁四矢:
Aμ=(A1A2A3A4)
这是一个矢量,前三个分量是磁矢势的三个空间分量,最后一个分量
A4=ciΦ
(3) 电磁场强:
Fμν=0−B3B2ciE1B30−B1ciE2−B2B10ciE3−ciE1−ciE2−ciE30,μ,ν=1,2,3,4
这是一个二阶反对称张量.
Lorentz 变换是正交线性变换,它的正交性保证了变换矩阵元满足:
aμαaμβ=δαβa~αμa~αν=aμαaνα=δμν(1)
但是此式不意味着变换矩阵对称,Lorentz 变换矩阵只是线性复正交和 Hermite 的.
注意
说明:
这里用的是 Lorentz boost 的虚时间表示,这样的表示用的是 x4=ict,能够把 Minkowski 空间变成真正的 Euclidean 空间. 在这样的表示下,Lorentz boost (换句话说,坐标的平移) 是不对称的,而且复正交.
但是标准 Lorentz 变换是用如下的表示:
dx1′dx2′dx3′dx4′=γ−βγ00−βγγ0000100001dx1dx2dx3dx4
这里用的是
x1x2x3x4=ctxyz
是实坐标的,显然其变换矩阵 (boost 部分) 是对称的,而且不是复正交的,而是伪正交的.
同时,标准 Lorentz 变换的「伪正交」条件是要求变换矩阵满足:
ΛTηΛ=η
其中 η 是 Minkowski 度规,η=diag(1,−1,−1,−1).
另外,Lorentz 变换不只有 boost (沿某一条轴的坐标平移),还有旋转的操作. 例如在标准 Lorentz 变换的表示中,一个绕 y 轴的 90° 旋转是:
Λ=1000000−100100100
这种变换矩阵不是对称的,但是是伪正交的.
广义相对论中的张量
因为广义相对论讨论的不是平直的时空,所以这里的坐标变换通常是非线性的,一般也不是正交的. 但是目前可以先丢开空间的平直性,在「仿射空间」中讨论一般的坐标变换.
「仿射」指线性,如果矢量满足可加性,则这个空间就是仿射空间;但是仿射空间中没有定义零矢量、曲率和挠率,所以我们不能讨论这个空间是不是平直的.
注意
上面是书中的定义. 实际上严谨的仿射空间定义是:
/Definition/
设 V 是域 F 上的矢量空间,且 A 是一个集合,其元素称作 点,并用 p˙,q˙,r˙,⋯ 表示. 称 A (或 (A,V)) 是和 V 相伴 (连带) 的仿射空间,若给定 Descartes 积 A×V 到 A 的映射 (记该映射的像 f(p˙,v) 为 p˙+v):
f:(p˙,v)↦p˙+v
其具有性质:
∀p˙∈A,∀u,v∈V,有 p˙+0=p˙,(p˙+u)+v=p˙+(u+v).
(存在零元,有结合律)
∀p˙,q˙∈A,有且仅有一个矢量 v∈V 使得 p˙+v=q˙. 通常用 pq 或者 q˙−p˙ 代表矢量 v.
并把 V 的维数 n 称为 A 的 维数,有时记成 An.
Wiki 上有一个帮助理解的非正式描述:
仿射空间像是没有原点的向量空间,其中的向量只有方向和大小.
若有甲、乙两人,甲认为空间的原点在 o 点,乙则认为原点在点 p. 现在要求两个向量 a 和 b (用点来表示向量,这里的向量指的是点和原点之间的差向量) 的和,那么两个人得到的结果不会是一样的.
另外,若两人分别计算 a 和 b 的线性组合,要求系数和为 1,那么两人将得到相同的结果. (就像我们高中所学的向量末端共线)
仿射空间就是要以相同的线性组合来描述同样的点,所以仿射组合的系数构成了一个「重心坐标」.
设四维仿射空间中的广义坐标变换:
x′μ=x′μ(xν),μ,ν=1,2,3,4
联系了两组广义坐标 x′μ,xν,其中 x4=ict. 这个函数关系可能很复杂,但是可以写出坐标微分的变换公式:
dx′μ=∂xα∂x′μdxα
仍然是重复指标代表求和,这样的重复指标又称傀儡指标 / 傀标.
提示
在广义坐标变换中,傀标只能由一个上标和一个下标组成.
(在分母上的上标算下标,在分母上的下标算上标)
如果变换矩阵行列式不为零:
det∂xα∂x′μ=0 or ∞
则逆变换存在,
dxα=∂x′μ∂xαdx′μ
变换系数满足
∂x′μ∂xα⋅∂xβ∂x′μ=∂xβ∂xα=δαβ∂xα∂x′μ⋅∂x′ν∂xα=∂x′ν∂x′μ=δμν
关于「上」和「下」标的问题,可见 .
另外,上下标有先后顺序,这仅仅是来源于上标下标需要排成一行,不能有重合的.
在广义相对论中,Lorentz 变换 aμν 对应:
aμν∼∂xν∂x′μ,(a−1)νμ∼∂x′μ∂xν
但是因为广义相对论中的广义变换矩阵不是正交矩阵,所以逆矩阵的形式更加复杂,也不一定满足 (1).
总结和狭义相对论的区别:
变换矩阵不一定是正交矩阵;
变换矩阵的矩阵元不再是常数.
(当然因为是逐点定义,所以微分形式的变换在某一个点处还是常数)
广义相对论中,零阶张量的定义仍然不变.
一阶逆变张 (矢) 量定义为「在广义坐标变换下像坐标微分一样变换的量」,
V′μ=∂xα∂x′μVα
坐标微分才是矢量,坐标本身不一定!
二阶逆变张量:「在广义坐标变换下按照下面规律变换的量」
T′μν=∂xα∂x′μ∂xβ∂x′νTαβ
n 阶逆变张量:
T′μν⋯λ=∂xα∂x′μ∂xβ∂x′ν⋯∂xσ∂x′λTαβ⋯σ
相对应地,有协变张量的定义,零阶定义不变,其他阶数有:
Vμ′Tμν′Tμν⋯λ′=∂x′μ∂xαVα=∂x′μ∂xα∂x′ν∂xβTαβ=∂x′μ∂xα∂x′ν∂xβ⋯∂x′λ∂xσTαβ⋯σ
协变张量和逆变张量的变换矩阵互为逆矩阵.
另外,还有混合张量,既有逆变指标又有协变指标,比如:
Tν1ν2⋯νq′μ1μ2⋯μp=∂xα1∂x′ν1⋯∂xαp∂x′μp⋅∂x′ν1∂xβ1⋯∂x′νq∂xβqTβ1β2⋯βqα1α2⋯αp
(其实应该写成 T′μ1μ2⋯μpν1ν2⋯νq 来表示先后顺序的… 不过这样疑似太长了)
有 p 个逆变指标 & q 个协变指标的张量称为 (p+q) 阶混合张量 / (p,q) 阶张量. 很明显,Kronecker 符号 δαβ 是 (1,1) 阶混合张量. Kronecker 符号满足:在任何坐标系下均有
δαβ=⎩⎨⎧10α=βα=β
可以在一个坐标系中定义,之后用混合张量的变换式得到任何坐标系下的 Kronecker 符号定义:
δ′μν=∂xα∂x′μ⋅∂x′ν∂xβδαβ=∂xα∂x′μ⋅∂x′ν∂xα=∂x′ν∂x′μ=⎩⎨⎧10μ=νμ=ν
因为狭义相对论是在线性正交变换下的,所以只有一类张量;但是广义相对论中有两类.
张量代数
(1) 加减法:必须同阶才能相加减,定义为相应分量相加减.
(2) 乘法:指「外乘」,外乘运算使张量阶数升高:
Cαβγμν=Aαβμ⋅Bγν
一个 (p1,q1) 阶张量和一个 (p2,q2) 阶张量相乘得到一个 (p1+p2,q1+q2) 阶张量.
(3) 缩并:让混合张量的一对上下标成为傀标,作求和. 比如 Cρτλμν 对 μ 和 τ 的缩并是
Cρλν=Cρμλμν
混合张量才能够缩并,缩并使张量的阶降低.
(4) 标积 (内积):外乘后再缩并,也就是
C=AμBμ
内积只能在逆变和协变之间进行.
(5) 对称性:关于一对上标 / 一对下标定义,若
Tαβγδμνσ=Tδβγαμνσ
则张量对下标 α 和 δ 对称. 若
Tαβγδμνσ=−Tαδγβμνσ
则张量对下标 β 和 δ 反对称.
提示
若称一个张量是对称 / 反称的,意味着它任何一对上标和任何一对下标都是对称 / 反称的.
反称张量的特点:反称指标取同一值的分量为零. 比如二阶反称张量写成矩阵时,对角元一定是零.
另外,任意一个二阶逆变 (/ 协变) 张量 Tμν (/ Tαβ) 都可以分解为一个对称张量 () 和一个反称张量 [] 的和:
Tμν=T(μν)+T[μν]
其中
T(μν)=2Tμν+Tνμ,T[μν]=2Tμν−Tνμ
警告
到这里我还有点没理解张量的物理实质是什么… 如果后面也没有理解,我可能需要在这个位置作补充.
平移 & 联络
张量逐点定义,如果要计算不同点之间张量之差,得到的不再是张量,会失去张量的各种变换性质. 但是我们需要研究相邻点之间张量的微小差值来得到张量的微分. 因此要新定义「差」,引入「矢量平移」和「仿射联络」的概念.
(1) 先来探索协变矢量的平移:
矢量场 Aμ 在相邻 P,Q 两点的值分别为 Aμ(P) 和 Aμ(Q),
/Definition/ (矢量平移)
P 点的矢量平移到 Q 点后,写作 Aμ(P→Q).
我们要求平移后的新矢量具有协变矢量的变换性质:
Aμ′(P→Q)=(∂x′μ∂xα)QAα(P→Q)(2)
虽然在 P 点 Aμ(P) 是协变的,但是在 Q 点 Aμ(P) 就不一定协变,因此 Aμ(P→Q) 和 Aμ(P) 之间有一个增量.
矢量平移要求:
- 平移后矢量 Aμ(P→Q) 是 Q 点的矢量;
- 平移引起的微元改变量 δAμ(P) 与位移 dxμ 呈线性.
(这样的矢量平移称为 Levi - Civita 平移)
所以有要求:
δAμ(P)≡Aμ(P→Q)−Aμ(P)=Γμνλ(P)⋅Aλ(P)⋅dxν
这里引入的比例系数 Γμνλ(P) 就是 P 点的仿射联络,建成联络. 定义了仿射联络的仿射空间称仿射联络空间.
注意
说明一下:下面用到的 Γμνλ 注意先后顺序的写法应该是 Γλμν,但是目前不注意先后顺序也没什么影响,所以先这么写了.
提示
一点理解:注意到这里有两次 Einstein 求和,对 λ 和 ν 求和,所以新的矢量分量会受到原来矢量各个分量的影响.
(2) 求联络在坐标变换下的变换性质,是要保证 (2) 式始终成立. 利用这个式子,有
(∂x′μ∂xα)Q=(∂x′μ∂xα)P+(∂x′ν∂x′μ∂2xα)Pdx′ν
理解
这玩意卡了我两个小时,然后反应过来我想多了. 一开始想的是这是不是下面的公式:
(∂B∂A)C=(∂B∂A)D+(∂D∂A)B(∂B∂D)C
但是并不是. 实际上这个公式来源于将 ∂xα/∂x′μ 看作一个随着 x′ν 变化的函数,再求一个微分而已.
这实在是太蠢了.
因此 (2) 式可以写作
Aμ′(P→Q)=((∂x′μ∂xα)+(∂x′μ∂x′ν∂2xα)Pdx′ν)⋅Aα(P→Q)
若利用 Γμν′λ 定义,写成:
Aμ′+Γμν′λ⋅Aλ′⋅dx′ν=((∂x′μ∂xα)P+(∂x′μ∂x′ν∂2xα)Pdx′ν)⋅(Aα+Γαγβ⋅Aβ⋅dxγ)=(∂x′μ∂xα+∂x′μ∂x′ν∂2xα∂xσ∂x′νdxσ)⋅(Aα+Γαγβ⋅Aβ⋅dxγ)
(这里都是在 P 点写的,所以把 Aμ′(P) 中标识位置的「(P)」去掉了,偏导数同理)
注意
为什么要在最后把 dx′ν 换成 ∂x′ν/∂xσ⋅dxσ?
这是因为之后要换傀标,然后合并成同一项,如果不更换的话,两边一个是 dx′ν 一个是 dxγ,处在不同的坐标下,怎么变都合并不了.
利用 Aμ′=∂xρ/∂x′μ⋅Aρ 和 dx′ν=∂x′ν/∂xσ⋅dxσ 得到:
Γμν′λ⋅∂x′λ∂xρAρ⋅∂xσ∂x′νdxσ=∂x′μ∂x′ν∂2xα⋅Aα⋅∂xσ∂x′νdxσ+∂x′μ∂xα⋅Γαγβ⋅Aβ⋅dxγ
这里已经将两边都有的 Aα 那一项去掉. 最后一项的傀标 γ 也可以换成 σ,再更换每一项中对矢量分量求和的傀标,原式可以合并为
(Γμν′λ∂x′λ∂xρ∂xσ∂x′ν−Γασρ∂x′μ∂xα−∂x′μ∂x′ν∂2xρ∂xσ∂x′ν)Aρdxσ=0
LHS 是两次对四维指标求和,相当于 16 项这样的括号. 因为这个式子对任意的 Aρdxσ 都是零,所以要求括号内始终为零. 这样就得到了仿射联络在坐标变换下的公式:
Γμν′λ=Γασρ∂x′μ∂xα∂x′γ∂xσ∂xρ∂x′τ+∂x′μ∂x′γ∂2xρ∂xρ∂x′τ
警告
这个公式实在是丑得可以… 注意求和的部分,下标太多容易搞混.
这也表明联络不是一种张量.
(3) 逆变矢量在平移下的增量:
和协变矢量很像,但是相差一个符号,
δAμ(P)≡Aμ(P→Q)−Aμ(P)=−Γλνμ⋅Aλ(P)⋅dxν
更高阶张量的平移我们兴趣不大.
总结一下联络的性质:
在同一个仿射空间中引入两种联络,1Γμνλ 和 2Γμνλ,虽然这两个都不是张量,但是它们的差 δΓμνλ 是 (1,2) 阶张量:
δΓμνλ=1Γμνλ−2Γμνλ
联络一般是非对称的,但是可以分为对称和反对称部分之和
Γμνλ=Γ(μν)λ+Γ[μν]λ
对称部分和反对称部分分别是
Γ(μν)λ=21(Γμνλ+Γνμλ),Γ[μν]λ=21(Γμνλ−Γνμλ)
对称张量称为对称联络,不是张量;但是反对称部分是张量,称为挠率张量.
联络一共有 4×4×4 个分量,对称部分有 40 个独立分量,反对称部分 (挠率张量) 有 24 个独立分量.
协变微商
标量场的协变微商
标量场 U(x) 的普通微商:
U,μ≡∂xμ∂U(x)
注意
这个「, 」作为一个微商符号属实有点诡异,不过既然是笔记,还是按照书本来罢.
P.S. 查了一下 Wiki 发现好像标准符号真的是这样,那没事了.
上面的普通微商变换到新坐标系:
U,μ′≡∂x′μ∂U′(x′)=∂xα∂U′∂x′μ∂xα=∂xα∂U∂x′μ∂xα=U,α∂x′μ∂xα
(其中中间一个等号的来源是 U′ 和 U 这两个函数形式是一样的)
因此可知,U,α 是协变矢量,不是标量场;这个「普通微商」就被称为「协变微商」. 用「; 」表示协变微商,对于标量场有
U;μ=U,μ
也就是协变微商等于普通微商.
协变矢量场的协变微商
协变矢量场的普通微商:
Aμ,ν≡∂xν∂Aμ≡Q→PlimΔxνAμ(Q)−Aμ(P)
但是空间中不同的两个点张量之差不一定是张量,所以普通微商不再具有张量性质.
而协变微商要用平移定义:
Aμ;ν≡Q→PlimΔxνAμ(Q)−Aμ(P→Q)
由平移定义,得到
Aμ;ν=Aμ,ν−ΓμνλAλ
这是协变矢量的协变微商. 值得注意,RHS 两项单独拿出来都不是张量,只有它们的差是张量.
协变微商的 Leibniz 法则
这是规定:
(A⋯⋯B⋯⋯);λ=(A⋯⋯;λ)(B⋯⋯)+(A⋯⋯)(B⋯⋯;λ)
协变微商和普通微商都服从 Leibniz 法则. 一个简单的例子是
(AμνσBβαγε);λ=Aμνσ;λBβαγε+AμνσBβαγε;λ
注意
到这里还是觉得张量微商这个概念有点不具体. 实际上把符号理解成分量,再把「;λ」这里后面的指标理解为微商定义里面要除掉的微元坐标的指标,就能想象出是个什么意思. 大概是某种张量场随着很多坐标变化,然后这个张量场的某个分量 μ (得是 ; 号前面的那个指标) 随着 xν 的改变而变化,所产生的那个叫做「微商」的东西 (换言之,变化率).
逆变矢量场的协变微商
逆变的指标在上面,直观地来讲,好像没有 ; 号前面的那个指标,所以我们想到要和协变矢量场配在一起写微商. Aμ(x) 和任意的一个协变矢量场 Bμ(x) 内积,得到标量场. 又知道标量场的协变微商就等于普通微商,那么
(AμBμ);λ=(AμBμ),λ
这时候用 Leibniz 法则 这下知道为什么要在这一节之前讲 Leibniz 法则了,可以得到
Aμ;λBμ+AμBμ;λ=Aμ,λBμ+AμBμ,λ
利用之前的协变矢量场协变微商公式,
Aμ;λBμ=Aμ,λBμ+ΓμλνAμBν
换傀标,同时矢量场 Bμ 是任意的,可以得到
Aμ;λ=Aμ,λ+ΓνλμAν
警告
这里协变微商的含义没有协变矢量场那么直观,因为定义式不是通过极限来做的. 不过理解为「对应」的关系倒可能也很不错.
高阶张量场的协变微商
类似地,对二阶张量:
Tμν;λTμν;λTμν;λ=Tμν,λ−ΓμλρTρν−ΓνλρTμρ=Tμν,λ+ΓρλμTρν+ΓρλνTμρ=Tμν,λ+ΓρλμTρν−ΓνλρTμρ
注意
可以看到,协变的指标对应一个「−」号,逆变的指标对应一个「+」号,额外项的求和都是对「被求导」的指标做的求和,这至少是一个记忆方法.
/Example/ (Kronecker 符号的协变微商)
Kronecker 符号是二阶混合张量,有
δμν;λ=δμν,λ+Γρλμδρν−Γνλρδμρ=δμν,λ
但是这个张量的分量完全是常数,所以直接得到协变微商为零.
测地线与仿射参量
在平直空间中,直线具有「自平行」性质,即线上的任意相邻两点的切矢量相互平行. 利用这一性质可以把直线概念推广到仿射空间,称为测地线.
四维空间中曲线的参数方程:
xμ=xμ(λ)
这里 λ 只是一个标志性的参量. 任意一点的切矢量定义为
Aμ=dλdxμ
这是一个逆变矢量. 刚刚说要比较相邻两点的切矢量是否平行,所以需要平移操作,平行要求:
Aμ(Q)=F(λ+dλ)Aμ(P→Q)
这里 F(λ+dλ) 只是一个系数,上面式子是在 Q 点做比较. 因为 P 点的切矢量肯定平行于 P 点自己的,所以 F(λ)=1,若定义
f(λ):=dλdF
则上面式子可以改写成
Aμ(Q)=[1+f(λ)dλ]⋅Aμ(P→Q)
满足这个式子的曲线称为 测地线 / 自平行线. 接下来的任务是求测地线方程. 利用平移矢量的关系,可得
Aμ(P→Q)=Aμ(P)−Γαβμ(P)⋅Aα(P)dxβ=dλdxμ+Γαβμdλdxαdλdxβdλ
另外,
Aμ(Q)=Aμ(P)+dAμ(P)=dλdxμ+dλ2d2xμdλ
所以测地线微分方程是
dλ2d2xμ+Γαβμdλdxαdλdxβ=f(λ)dλdxμ
简化
在参量选择比较好的情况下,测地线方程可以简化. 假设另一个标量参量 σ,有参量变换 λ=λ(σ),我们知道
dλdxμdλ2d2xμ=dσdxμ⋅dλdσ=dσ2d2xμ⋅(dλdσ)2+dσdxμ⋅dλ2d2σ
于是
[dσ2d2xμ⋅(dλdσ)2+dσdxμ⋅dλ2d2σ]+Γαβμ(dλdσ)2dσdxαdσdxβ=f(λ)dσdxμdλdσ(dσ2d2xμ+Γαβμdσdxαdσdxβ)(dλdσ)2=[f(λ)dλdσ−dλ2d2σ]⋅dσdxμ
如果参量 σ 满足
f(λ)dλdσ−dλ2d2σ=0(3)
则上面式子简化为
dσ2d2xμ+Γαβμdσdxαdσdxβ=0
称满足 (3) 的参量 σ 为仿射参量,采用这种参量时,f(σ)=0,平行条件是直接相等.
值得注意的是,仿射参量并不唯一,τ=aσ+b 都是仿射参量.
曲率与挠率
我们已经知道联络的反称部分是挠率张量. 现在要引入一个新的由联络构造的张量 —— 曲率张量. 这两个量是决定空间几何性质最重要的量.
(1) 曲率张量的引入:对于给定的协变矢量场 Aλ(x),求两次协变微商 Aλ;μ;ν 可得
Aλ;μ;ν=Aλ;μ,ν−ΓλνρAρ;μ−ΓμνρAλ;ρ=Aλ,μ,ν−Γλμ,νρAρ−ΓλμρAρ,ν−ΓλνρAρ,μ+ΓλνρΓρμσAσ−ΓμνρAλ;ρ
注意
可以很明显地看出「Aμ;λ」这个符号的好处:这可以看作一个二阶的张量,然后得到第一个等号后面的结果.
对于第二个等号,过程应该是:
LHS=(Aλ,μ−ΓλμρAρ),ν−ΓλνρAρ;μ−ΓμνρAλ;ρ
然后分别展开得到上述结果. 上面没有展开最后一项的原因是后面并没有展开的必要性.
交换协变微商的顺序,也就是求 Aλ;ν;ν,得到
Aλ;ν;μ=Aλ,ν,μ−Γλν,μρAρ−ΓλνρAρ,μ−ΓλμρAρ,ν+ΓλμρΓρνσAσ−ΓνμρAλ;ρ
这两者相差:
Aλ;μ;ν−Aλ;ν;μ=RλμνρAρ−2Γ[μν]ρAλ;ρ
其中
Rλμνρ≡Γλν,μρ−Γλμ,νρ+ΓσμρΓλνσ−ΓσνρΓλμσ
而联络的反称部分 Γ[μν]ρ=(Γμνρ−Γνμρ)/2 是挠率张量,等式左右两边都得是张量,所以 Rλμνρ 必须要是一个张量,这被称为 曲率张量.
注意
张量的协变微商是个张量,因为在求协变微商的过程中,所有联络系数产生的非齐次项都被添加的那些项抵消了. 再者,从定义完全可以验证协变微商的变换规律.
从上面可以看出,只有曲率和挠率都是零时 (或许可以理解为空间是平直的?),协变矢量的二阶协变微商才可以交换顺序,当然这一结论对逆变矢量、更高阶张量的协变微商均成立.
(2) 挠率的几何意义:
如下图,空间中从 O 点出来的两个无穷小位移,分别是 dxμ∼OQ′ 和 δxμ∼OQ,现在把 dxμ 平移距离 δxμ 到 Q 点,得到 QP;再把 δxμ 平移距离 dxμ 到 Q′ 点,得到 Q′P′. 在 Euclidean 空间中,P 和 P′ 肯定重合,但是空间如果是弯曲的,那么情况会不一样.
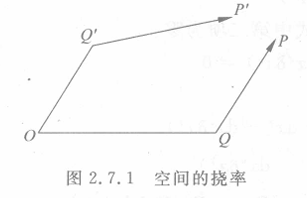
我们知道,
QPQ′P′=dxμ−Γλνμdxλδxν=δxμ−Γλνμδxλdxν
可计算 P 和 P′ 两点之差:
Δ=OQ+QP−(OQ′+Q′P′)=δxμ+(dxμ−Γλνμdxλδxν)−[dxμ+(δxμ−Γλνμδxλdxν)]=(Γνλμ−Γλνμ)δxνdxλ=2Γ[νλ]μδxνdxλ
这是一个二阶的偏移,体现挠率的作用.
(3) 曲率的几何意义:讨论无挠率的情况. 这个时候原来的四边形是闭合的,再考虑另一个矢量 Aμ,让它从 O 点开始沿这个闭合路径平移,经历 O→Q→P→Q′→O.
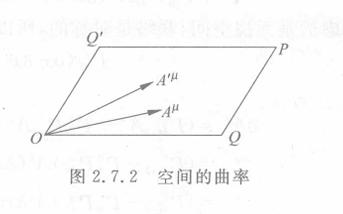
回到 O 点后,Aμ 变为 A′μ=Aμ+δAμ. 有
δAμ=A′μ−Aμ=Aμ(O→Q→P→Q′→O)−Aμ=Aμ(O→Q→P)−Aμ(O→Q′→P)
分别计算这两项:
Aμ(O→Q)Aμ(O→Q→P)=Aμ−ΓλνμAλδxν=(Aμ−ΓλνμAλδxν)−Γαβμ(Q)(Aα−ΓτσαAτδxσ)(dxβ−Γργβdxρδxγ)=Aμ−ΓλνμAλδxν−Γαβμ(Q)Aαdxβ+Γαβμ(Q)ΓτσαAτδxσdxβ−Γαβμ(Q)Γργβdxρδxγ
这里省略了本来应该有的「(O)」,因为大多数比较都是在 O 点进行. 我们知道联络的微分是
Γαβμ(Q)=Γαβμ(O)+Γαβμ,γ(O)δxγ=Γαβμ+Γαβμ,γδxγ
代入,最终得到
Aμ(O→Q→P)=Aμ−ΓλνμAλ(δxν+dxν)−Γλνμ,γAλdxνδxγ+ΓλνμΓργνAλdxρδxγ+ΓλνμΓργλAρδxγdxν
(这里利用了傀标的可替换性)
同理,
Aμ(O→Q′→P)=Aμ−ΓλνμAλ(dxν+δxν)−Γλνμ,γAλδxνdxγ+ΓλνμΓργνAλdxγδxρ+ΓλνμΓργλAρdxγδxν
差值为
δAμ=Γλνμ,γ(δxνdxγ−dxνδxγ)+ΓλνμΓργνAλ(dxρδxγ−dxγδxρ)+ΓλνμΓργλAρ(δxγdxν−dxγδxρ)
因为挠率为零 (这是我们的假设,在开头说过了),所以 RHS 第二项为零,有
δAμ=(Γλνμ,γAλ−ΓλνμΓργλAρ)(δxνdxγ−dxνδxγ)=(Γλνμ,γ−ΓσνμΓλγσ)Aλ(δxνdxγ−dxνδxγ)=(Γλνμ,γ−ΓσνμΓλγσ)Aλδxνdxγ−(Γλνμ,γ−ΓσνμΓλγσ)Aλδxνdxγ=−RλνγμAλδxνdxγ
这里就出现曲率了!
警告
这个曲率的定义式真有点难记,意义也不是很明显…
由上面的计算,可见只有在曲率为零的空间,一个逆变矢量沿无穷小环路平移一周,才能不附加转动地与原矢量重合,这就是曲率产生的几何效应. 对于曲率和挠率都是零的空间,一定可以找到一个坐标系,使得联络的所有分量在这个坐标系中都是零.
(4) 空间的平直性:因为挠率和曲率都是张量,所以它们的作用和坐标系的选取没有关系,如果挠率和曲率在某个坐标系里所有分量都是零,那么换任何坐标系都是如此,因此它们是空间的内禀性质;反之,联络并不是张量,所以即使是在平直空间中,换坐标系也有可能出现非零的联络.
(5) 曲率的两个性质:
曲率张量的后一对指标反称:
Rλμνρ=−Rλνμρ
曲率张量只有两种独立的缩并方式:
1、2 指标缩并
Aμν=Rλμνλ
1、3 指标缩并
Rμν=Rμλνλ
1、4 缩并和 1、3 缩并只差一个负号 (正是因为第一个性质),所以不是独立的.
我们把挠率不为零的空间称为扭曲的,曲率不为零的空间称为弯曲的. 在之后的讨论中,我们会很少提到挠率,一般默认挠率为零.
度规张量
引入联络之后还需要度量,也就是引入度规和距离. 引入度量的仿射空间称为 Riemann 空间,这里的几何就是 Riemann 几何.
距离与度规
用二次型
ds2=gμνdxμdxν
来定义空间中的距离 ds (也可以叫「线元」). 我们想要让距离是一个标量,因此这里度规 gμν 必须要是一个二阶协变张量;另外,dxμ 和 dxν 地位对等,所以 gμν 还要是对称张量.
下面是一些具体的度规例子.
/Example/ (三维 Euclidean 空间)
用直角坐标,线元是
ds2=dx2+dy2+dz2
度规张量便是
(gij)=100010001,i,j=1,2,3
如果使用球坐标,线元表达式是
ds2=dr2+r2dθ2+r2sin2θdφ2
度规张量
(gij)=1000r2000r2sin2θ,i,j=1,2,3
注意
怎么这里度规张量是 3×3 的?啊这是三维 Euclidean 空间.
/Example/ (四维 Minkowski 空间)
这里线元是
ds2=−(dx0)2+(dx1)2+(dx2)2+(dx3)2
度规张量
(gμν)=(ημν)=−1000010000100001,μ,ν=0,1,2,3
度规的正则形式与幺正基
一般来说,Riemann 空间中的度规分量 gμν 随着坐标的变化不是常数. 如果是常数,且 det∣gμν∣=0,则一定可以找到一个坐标变换,把二次型 ds2=gμνdxμdxν 化成坐标微分的平方和 (或差) 的形式,使度规张量在新坐标系下的分量为
gμν=⎩⎨⎧±1μ=ν0μ=ν(4)
注意
书中未证明这一定理. 实际上,证明并没有特别困难. 考虑一个新的坐标系,它和之前的坐标系之间相差一个线性变换,
yα=Lαμxμ+cα,dyα=Lαμdxμ
定义 Lαμ 的逆矩阵是 Mμβ,有 LαμMμβ=δαβ 和 MαμLμβ=δαβ. 这时,新的坐标系下,线元表示为
ds2=gμνdxμdxν=(gμνMμαMνβ)dyαdyβ
新的度规就是 gμνMμαMνβ=gαβ′,这相当于对原来的度规矩阵进行合同变换 MTgM.
合同变换本质上是改变二次型的基.
根据线性代数中的 Sylvester 惯性定律,存在可逆矩阵 M 使得
MTgM=η
其中 η 是对角元素为 ±1 的对角阵,同时正负号的数量在合同变换下不变.
通过选择 M 为 Sylvester 惯性定律给出的那个矩阵,新的度规就是 gαβ′=ηαβ,满足
gαβ′=ηαβ=⎩⎨⎧±10α=βα=β
证毕.
(4) 式叫做度规张量的正则形式,把 gμν 表为正则形式的坐标基叫正交归一基或者幺正基. 但是,当且仅当 Riemann 空间平直时度规才能在全空间变换为正则形式. 当然,在空间中某一点 P 邻域,因为度规 gμν(P) 几乎是常数,所以可以局部地变为正则形式,这就说明 Riemann 空间可以看作是局域平直的.
时空与号差
在之前的例子中,三维 Euclidean 空间的度规张量非对角元都是零、对角元全为正,这是 正定度规. 而四维 Minkowski 空间中的度规张量非对角元是零,但是对角元不全是正的,这是 不定度规.
我们定义:正则形式下,度规分量对角元之和称为度规的号差. Minkowski 空间的号差为 +2,这是显而易见的. 但是这个概念推广到四维 Riemann 空间时,必须逐点把度规化为正则形式,计算号差. 由之前在 Minkowski 空间中得到的经验,三个「正对角元」对应的是空间,剩下的「负对角元」对应的是时间,这就区分了时空;号差为 +2 的四维 Riemann 空间,就被称为 Riemann 时空.
注意
号差是人为定义的,当然可以定义 −2 作为时空的号差. 但是这本教材定义的是 +2,所以之后统一用 +2.
弯曲的 Riemann 时空可以逐点建立局域的 Minkowski 坐标系.
张量指标的升降
先定义逆变度规张量,以便之后用度规来升降张量的指标.
协变度规张量的行列式 g≡det∣gαβ∣,代数余子式写成 Δαβ. 若 g=0,可以定义逆变度规张量:
gαλ:=gΔαλ
它满足
gαλgλβ=gΔαλ⋅gλβ=δαβ
协变度规张量可以降低逆变指标:
Aα≡gαβAβ,Tαβ≡gαλTλβ
逆变度规张量可以升高协变指标:
Aα≡gαβAβ,Tαβ≡gαλTλβ
于是可以定义坐标微分的协变形式,
dxα:=gαβdxβ
所以之后写「距离 (线元)」就可以写成 AαAα (dxαdxα) 了!同时我们还可以发现,Kronecker 符号其实是度规的混合形式:
gαβ=δαβ
因为:
gαβ=gαλgλβ=⎩⎨⎧gαλ0λ=βλ=β=gαλδλβ
Christoffel 符号
几个问题:联络和度规之间有无联系?矢量平移在 Euclidean 空间中不会改变长度,如何在仿射空间中保持这一性质?
矢量平移有:
Aμ(P→Q)=Aμ(P)−Γνλμ(P)Aν(P)dxλ
现在我们想要求平移不改变长度,所以要求
gμν(Q)Aμ(P→Q)Aν(P→Q)≡gμν(P)Aμ(P)Aν(P)
将平移公式和 gμν(Q)=gμν(P)+gμν,λ(P)dxλ 代入,保留一阶:
注意
这里用普通微商而非协变微商是因为纯粹是在使用普通微商的定义罢了.
[gμν+gμν,λdxλ](Aμ−ΓσγμAσdxγ)(Aν−ΓαβνAαdxβ)gμν,λAμAνdxλ−gμνΓσγμAσAνdxγ−gμνΓαβνAαAμdxβ(gμν,λAμAν−gμνΓσλμAσAν−gμνΓαλνAαAμ)dxλ(gμν,λ−gανΓμλα−gμβΓνλβ)AμAνgμν,λ−gανΓμλα−gμβΓνλβ=gμνAμAν=0=0=0=0
上述三个指标可以轮换,得
gλμ,ν−gαμΓλνα−gλβΓμνβgνλ,μ−gαλΓνμα−gνβΓλμβ=0=0
前两式相加减去第三式:
(gμν,λ+gλμ,ν−gνλ,μ)−gανΓμλα−gμβΓνλβ−gαμΓλνα−gλβΓμνβ+gαλΓνμα+gνβΓλμβ=0
注意到度规张量是对称的,而其中后六项在交换度规张量指标后 (或者不交换时) 可以视为给联络降逆变指标:
(gμν,λ+gλμ,ν−gνλ,μ)−gναΓμλα−gμβΓνλβ−gμαΓλνα−gλβΓμνβ+gλαΓνμα+gνβΓλμβ(gμν,λ+gλμ,ν−gνλ,μ)−Γνμλ−Γμνλ−Γμλν−Γλμν+Γλνμ+Γνλμ=0=0
注意
到这里似乎已经走投无路了:我们怎么进一步化简?但是想到我们很久之前提到的,我们目前讨论的时空是没有挠率的,是弯曲的时空,而非扭曲的时空. 因此,多了一个极为重要的条件,那就是:联络关于下标对称.
有了这个条件,可以很轻松地进一步推导.
(虽然我在这里卡了半个晚上,最后感谢超理讨论环的学长「银龙 ~ iungrdvgtd」略加点拨. 不过要我说,书中直接讲「注意到联络的对称性」确实欠妥,毕竟毫无提示.)
最终得到无挠 Riemann 空间中,在保持矢量长度平移不变性的条件下,对称联络与度规的泛函关系:
ΓλμνΓμνα≡21(gμλ,ν+gνλ,μ−gμν,λ)=21gαλ(gμλ,ν+gνλ,μ−gμν,λ)
满足此式的联络,称为 Christoffel 符号;这个式子在广义相对论中极为常见,因为广义相对论所用的时空就是无挠率的 Riemann 时空.
在推导的过程中,我们还可以发现一些额外的结果,比如:
gμν,λ−gανΓμλα−gμβΓνλβ=0
其实意味着 gμν;λ=0 (度规张量的协变微商为零),所以逆变度规张量的协变微商也是零,混合度规张量也是. 这个可以作为 Riemann 空间中矢量长度具有平移不变性的一个条件.
到这里,我们终于可以回顾一下物理的内容:注意到可以证明如下的定理
/Theorem/
对无挠 Riemann 时空中的任何一点,都可以找到一个坐标变换,把那一点的 Christoffel 符号的所有分量都变到零.
注意
书中又略去了证明. 尝试证明如下:首先考虑到联络的变换规则是
Γμν′λ=Γασρ∂x′μ∂xα∂x′γ∂xσ∂xρ∂x′τ+∂x′μ∂x′γ∂2xρ∂xρ∂x′τ
如果坐标变换是:
xμ=x′μ−21Γαβμx′αx′β
先来计算各阶导数 (这里可以通过改变原点使得在该点 xα≡0),
∂xα∂x′μ∂x′σ∂xλ∂x′α∂x′β∂2xμ=δμα=δλσ=−Γαβμ
代入变换公式,发现可以做到 Christoffel 符号的所有分量为零.
因为联络的所有分量为零 = 测地线方程是直线;而不全为零时测地线不是直线,所以联络相应于「引力场强 / 惯性场强」. 上面的定理在这样的理解下,就变成对于无挠 Riemann 时空中的任何一点,都可以找到一个局域的自由落体坐标系. 所以这个定理就是等效原理的数学基础.
而有挠率的空间找不到这样的变换,因为挠率是张量,不可能通过坐标变换把它的所有分量都变成零,因此我们的时空只能是无挠率的.
短程线
在 Euclidean 空间中,短程线是直线;现在利用变分求 Riemann 空间中两点间的短程线.
定义泛函
S=∫ABds
作为连接 A 和 B 的曲线长度. 短程线满足变分为零,也就是
δS=δ∫ABds=0
而 ds=(gαβdxαdxβ)1/2,若引入一个标量 λ 来描述曲线 xμ=xμ(λ),上式可以化为
ds=(gαβdλdxαdλdxβ)1/2dλ=(gαβx˙αx˙β)1/2dλ=Ldλ
\dot{} 是导数的简写,最后一个等号则定义了 Lagrange 函数.
变分的 Euler - Lagrange 方程为
∂xν∂L−dλd∂x˙ν∂L=0
代入 L 得到
gαβx˙αx˙β1∂xν∂gαβx˙αx˙β=dλd(gαβx˙αx˙βgανx˙α+gνβx˙β)=dλd(gαβx˙αx˙β2x˙ν)
如果取 λ 为曲线长度 s,那么
gαβx˙αx˙β=gαβdsdxαdsdxβ=1
(因为曲线长度本身随着曲线长度的增长率就是 1) 这简化了方程,
21gαβ,νx˙αx˙β21gαβ,νx˙αx˙βgανds2d2xα=dsd(gανx˙α)=gανds2d2xα+dxβdgανdsdxβdsdxα=(21gαβ,ν−gαν,β)dsdxαdsdxβ
注意到这里 RHS 的 α 和 β 指标完全对称,有
gαν,β=21(gαν,β+gβν,α)
于是
gανds2d2xα+21(gαν,β+gβν,α−gαβ,ν)dsdxαdsdxβds2d2xμ+21gμν(gαν,β+gβν,α−gαβ,ν)dsdxαdsdxβ=0=0
和我们定义的 Christoffel 符号一致,最终得到
ds2d2xμ+Γαβμdsdxαdsdxβ=0
这和我们之前定义的测地线方程完全一致,唯一的区别在于这里的联络多了 Christoffel 符号的限制,只能在无挠率的 Riemann 时空中成立,而且是关于下标对称的.
在无挠率 Riemann 时空,测地线就是短程线.
警告
上面推导给了我们一个启发:测地线可以用「长度」作为参数,这是仿射参量.
但是之后会遇到的描述光线的「零测地线」,因为其「长度」为零,所以 ds=0,不能作仿射参量.
Riemann 空间的曲率张量
仍然在无挠率的空间讨论.
曲率张量的对称性
在 曲率与挠率 中给出了曲率张量和联络的关系:
Rλμνρ=Γλν,μρ−Γλμ,νρ+ΓσμρΓλνσ−ΓσνρΓλμσ(5)
而且得到了反对称性,也就是 Rλμνρ=−Rλνμρ. 在无挠率的空间,曲率张量会有很多更好的性质,为方便讨论,引入 (0,4) 型表示 (降逆变指标):
Rρλμν≡gρσRλνμσ
可以证明这一表示有几个性质:
后一对指标反对称;
前一对指标反对称;
前一对指标与后一对指标对称;
Ricci 恒等式:
Rλμνρ+Rμνλρ+Rνλνρ=0,Rρλμν+Rρμνλ+Rρνλν=0
三个派生的重要张量
曲率张量缩并可以得到三个重要张量:
(1) Ricci 张量:我们已经知道曲率张量只有两种独立的缩并方式,但是在 Riemann 空间中,Christoffel 符号的对称性增加了曲率张量的对称性,有
Aμν=Rλμνλ=0
注意
书中没说理由,来直接用定义算一下:
Rλμνλ=Γλν,μλ−Γλμ,νλ+ΓσμλΓλνσ−ΓσνλΓλμσ=∂xμ∂Γλνλ−∂xν∂Γλμλ+ΓσμλΓλνσ−ΓσνλΓλμσ
现在先看后两项,第三项
ΓσμλΓλνσ=ΓλμσΓσνλ=ΓσνλΓλμσ
只是改变了傀标,和第四项完全相同,所以原式化为
Rλμνλ=∂xμ∂Γλνλ−∂xν∂Γλμλ
其实到这里可以发现,因为 Rλμνλ 关于后一对协变指标对称,所以已经可以得到 Rλμνλ=0. 但是我一开始是问了 DeepSeek,它告诉我了一些别的计算,所以我还是写下来.
难点落在求 Γλνλ 上. 这时考虑 Christoffel 符号的定义,
Γλνλ=21gλσ(gλσ,ν+gνσ,λ−gλν,σ)
注意到后两项
gλσgνσ,λ−gλσgλν,σ=gσλgνλ,σ−gλσgλν,σ=gλσgλν,σ−gλσgλν,σ=0
(第一个等号只是改变了第一项的傀标,第二个等号是利用度规张量的对称性) 所以可以得到
Γλνλ=21gλσgλσ,ν
为了更好计算,我们引入 g=det∣gλσ∣. 由线性代数的结论,
∂Aij∂det(A)=det(A)(A−1)ji
于是
∂gλσ∂g∂xν∂g⟹gλσgλσ,ν=g⋅gλσ=∂gλσ∂ggλσ,ν=ggλσgλσ,ν=∂xν∂ln∣g∣
原来的曲率张量缩并变为
Rλμνλ=21(∂xν∂xμ∂2−∂xμ∂xν∂2)ln∣g∣=0
证毕.
到这里为止我收获最大的就是换傀标名称这个操作,有时候有奇效,这就是对称性的魅力.
上面证明了不能缩并逆变指标和第一个协变指标,因此我们只剩下一种缩并,这种缩并得到的张量称为 Ricci 张量:
Rμν=Rμλνλ
Ricci 张量对称:
Rμν=gλρRρμλν=gλρRλνρμ=gρλRλνρμ=Rνρμρ=Rνμ
(又是利用对称性)
(2) 曲率标量:Ricci 张量的缩并称为曲率标量,
R=gμνRμν=Rμμ
(3) Einstein 张量:这是 Einstein 引入的一个对于广义相对论很有用的张量,
Gμν≡Rμν−21gμνR
曲率张量的独立分量
讨论下面几种情况:(已经确认四个指标全部相同一定是 0)
四个指标只有两个不同值:由反对称,
Rμμμν=Rμμνν=0
只有唯一的独立排列 Rμνμν. 这种情况下不为零的独立分量个数是
1×Cn2=2!(n−2)!n!
(这里的 n 是维数,第一个因子是排列的可能数,第二个因子是维度中选出 2 个不同值的可能数)
四个指标中有三个不同值:从 n (维度) 中取三个数作为指标,有 Cn3 种取法,剩下一个一定和这三个中的一个相同. 因为前后两对分别反对称,所以相同的两个指标不能同时在前也不能同时在后,于是是一前一后. 但是后一对和前一对对称,所以只有一种独立排列;但是第四个指标有三种选择,所以独立分量数是
3×1×Cn3=2!(n−3)!n!
(第一个因子是第四个指标的可能选择数,第二个因子是排列的可能数,第三个因子是维度中选出 3 个不同值的可能数)
四个指标全部不同:不考虑 Ricci 恒等式,Cn4 种取法中每一种组合都对应三种独立排列方式 (原本是 A44=24 种排列,后一对和前一对对称,减少一半排列数;前后两对分别反对称,独立排列数再减为原来的 1/4,最后剩了 3 种独立排列),再考虑 Ricci 恒等式,减少一个独立排列,最后剩下 2 种.
独立分量数:
2×Cn4=4!(n−4)!2×n!
(第一个因子是每一种取法对应的排列可能数,第二个因子是维度中选出 4 个不同值的可能数)
综上所述,独立分量个数有
N=Cn2+3Cn3+2Cn4=12n2(n2−1)
简单计算可知 N(4)=20,N(3)=6,N(2)=1.
另外,Ricci 张量和 Einstein 张量都是对称张量,独立分量个数是
N=n+(n−1)+⋯+1=2n(n+1)
(就是左下角的三角形种分量的个数) 在 4 维空间它有 10 个独立分量.
曲率标量是不变量,只有一个独立分量.
空间的平坦性
因为已经有挠率为零了,如果这时候曲率张量所有分量全是零,那么一定能找到一个坐标,这里面 Christoffel 符号的所有分量为零 (见 定理),
定理 的证明
之前似乎没有证明这个定理,在这里简单说明一下 (避免之后我自己看不懂):首先选择 P 点的一组坐标基,因为没有曲率和挠率 (矢量的平行移动结果与路径无关),可以通过矢量从 P 点开始的平行移动来生成一个全空间的矢量场.
之后可利用线性代数中的结论证明这个坐标基和原来坐标系的基矢量对易,因此可以作为新坐标系的基矢量,在新坐标系联络为零.
联络分量全部为零 ⟺ 度规张量普通微商 gμν,λ=0,也就是说度规张量分量全是常数,这样的空间是 平坦的,度规可以化成 Minkowski 度规.
曲率张量分量全部为零是空间平坦性的判据.
Bianchi 恒等式
从曲率张量的定义式 (5) 出发,可以得到所谓的 Bianchi 恒等式:
Rλμν;σρ+Rλνσ;μρ+Rλσμ;νρ=0
/Proof/
张量关系式不随坐标系而改变,为方便,选择 P 点处联络为零的坐标系. 显然在 P 点有
Rλμν;σρ=Rλμν,σρ
也就是
Rλμν;σσ=(Γλν,μρ−Γλμ,νρ),σ+(ΓαμρΓλνα−ΓανρΓλμα),σ=(Γλν,μρ−Γλμ,νρ),σ=Γλν,μ,σρ−Γλμ,ν,σρ
没挠率的话后面两项似乎一直是零,其实根本没必要写出来罢. 同理可以计算 Bianchi 恒等式里的另外两项,相加就证明了恒等式.
缩并 Bianchi 恒等式的指标 ρ 和 σ,并利用 Ricci 张量的定义,得到
Rλμν;σσ+Rλνσ;μσ+Rλσμ;νσRλμν;σσ−Rλσν;μσ+Rλσμ;νσRλμν;σσ−Rλν;μ+Rλμ;ν=0=0=0
两边同时乘以 gνλ,因为 gνλ;α=0 所以可以很容易凑出全微分,得到
Rμ;σσ−R;μ+Rμ;νν=0⟹2Rμ;νν−R;μ=0
定睛一看,这和 Einstein 张量有类似的形式,所以有下面三种表述:
(Rνμ−21δνμR);ν(Rμν−21gμνR);ν(Rμν−21gμνR);ν=0=0=0
这表明 Einstein 张量的协变散度为零.
几个重要的运算
提示
内心 OS:终于到这里,这章快要结束了.
度规的微分
(欸这个我是不是之前已经用到了?证明 Ricci 张量是曲率张量的唯一缩并 的时候)
设 g=det∣gμν∣,Δμν 为 gμν 的代数余子式,有
gδνα=gαρΔνρ
逆变度规张量的定义就是 gμν≡Δμν/g,所以这里可以得到
∂gμν∂g=Δμν=ggμν
于是
dg=g⋅gμνdgμν=g⋅[d(gμνgμν)−gμνdgμν]=−g⋅gμνdgμν
利用了一下 gμνgμν 全微分为零.
注意
这时候有人要问了:之前不还是偏导数吗,怎么到这里不写 ∂ 开始写 d 了?
A:要知道,这可是 Einstein 求和啊,当然写出来的是全微分.
此外,还得到了我刚刚用到了的式子:
∂xσ∂g=g⋅gμνgμν,σ=−g⋅gμνgμν,σ
这些运算和之前提到过的「度规张量协变微商为零」都是广义相对论中常用的计算.
一个特殊的 Christoffel 符号
Γαμμ=21gμνgμν,α=−21gμνgμν,α=2g1∂xα∂g=∂xα∂ln∣g∣
这个也是和上面一样,在 这里 用到过了. 另外,因为我们规定好了号差,所以这里可以直接写 ∣g∣=−g.
散度的运算
和 Euclidean 空间类似,但是用协变微商换掉普通微商 (毕竟要得到一个标量). 散度运算使张量降阶,而且要注意的是:对协变指标求散度,定义为把指标升高之后再求散度.
逆变矢量的散度:
divAμ=Aμ;μ=Aμ,μ+ΓαμμAα=−g1∂xμ∂(−g⋅Aμ)
d'Alembert 算子:
□Φ=div(gradΦ)=div(gμν∂xν∂Φ)=−g1∂xμ∂(−g⋅gμν∂xν∂Φ)
二阶逆变张量的散度:
Cμν;ν=−g1∂xν∂(Cμν−g)+ΓνσμCνσ
如果这个二阶逆变张量反称,那么后面一项显然为零,注意到这一点可以简化计算.
旋度的运算
和散度一样,也应该用协变微商代替普通微商. 但是可以证明,这里用哪一个都是一样的 (简单想一下,就是做差的时候多的一项被抵消掉了,比较显然). 所以旋度运算和 Euclidean 空间完全一致.
旋度运算使得协变矢量场变成二阶反称张量场,使二阶反称张量场变成三阶反称张量场.
curlμνAμcurlμνAμν≡Aμ;ν−Aν;μ=Aμ,ν−Aν,μ≡Aμν;τ+Aντ;μ+Aτμ;ν=Aμν,τ+Aντ,μ+Aτμ,ν
体元的变换
赝张量定义为
Tμν=∣α∣α∂x′ρ∂xμ∂x′σ∂xνT′ρσ
式中,α 为坐标变换矩阵的行列式,∣α∣ 为 α 的绝对值. 对于不含反射的坐标变换,α/∣α∣=+1,这时赝张量的变换和张量相同;有反射变换,系数就是 −1,赝张量的变换比张量变换多一个负号.
不加证明地指出,体元在坐标变换下的规律是:
−g⋅d4x=∣α∣α−g′⋅d4x′
体元是赝标量.
2025/09/02 - 02:31,终于结束这一章的阅读笔记了. 之后来做习题. 由于我的 Typora 在将近 1.7w 字的重压下已经不堪重负,我决定单开一篇笔记来写习题. 这章 (或者说这整本书) 的习题并不多,如果之后都是单开一篇笔记来写习题,我想可以写得更详细些.
更新日志
2025/10/9 02:50
查看所有更新日志
f85b5-build(theme): update theme to rc-168于bc36a-feat(note): hope this is the last update of GR chapter-2于967a8-feat(note): update GR chapter-2于53eab-feat(note): update GR chapter-2于921db-feat(note): update GR chapter-2于c9b1c-feat(note): update self-learn-GR chapter-2于b0d2e-feat(note): update GR chapter-2于ed330-feat: update于70b9a-feat(note): update于cace8-feat(note): update于a13eb-feat(note): update于74d61-feat(notes): update于99c50-feat(notes): update于1902b-feat(note): add self-learn-GR于
