菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 4 二态系统

复制页面

约 2078 字大约 7 分钟

2025-10-12

上节课我们最重点讲的是化学势，这是因为在生命过程中需要进行很多化学反应. 我们说到化学平衡时有平衡常数等等，另外，如果想要研究系统的演化，我们可以来考虑系统的 kinetic 效应.

平衡态是一种特殊的稳态，不仅使得系统稳定，而且还要能够找到一种能量函数在这个状态下达到极值. 一个例子是我们上节课说到的细致平衡，在一个 A,B,CA,B,C 三种物质的环形反应链中，每一对反应都达到平衡才是所谓的细致平衡，这要求

k1k2k3k−1k−2k−3=1\frac{k_1k_2k_3}{k_{-1}k_{-2}k_{-3}}=1

这种情况下能够找到一种势能函数. 反之，如果这个体系有所谓的「旋度」，也就是有静流，那么就一定无法找到这样的势能函数.

如果大家学过图论，我们会知道一个「好的」图在每一个环路中都满足类似上面的平衡条件.

如何破坏这种平衡？我们举 ATP 的例子，在生物体内的 ATP 浓度很高，它在一个循环的反应中不断地加入，用渗透压来驱动反应向某一个特定方向旋转.

Michaelis-Menten 反应，这是一种酶催化反应：酶不参与反应，自由的酶 + 结合的酶 = 总量，

[E]+[ES]=Etot[E]+[ES]=E_{\text{tot}}

下面我们来用一下我们已经学到的上一章知识. 考虑二态系统，比如 DNA 复制时酶的结合与不结合、神经上电压的高于阈值与低于阈值等.

最简单的二态系统是我们的离子通道：打开和关闭. 为这两个态赋予两个能量，

e−βεclosed ,e−β(εopen−τΔA)e^{-\beta\varepsilon_{\text{closed}}}\,,\quad e^{-\beta(\varepsilon_{\text{open}}-\tau\Delta A)}

对于打开的离子通道，可能会有其他效应来进行一些调控，比如人体的触觉感知，在受到压力时细胞膜可能被拉伸，让这个离子通道被拉得更开. 因此为了描述这个效应，我们在上面的 open 态加入了一个由表面张力系数 τ\tau 和细胞膜面积变化 ΔA\Delta A 构造的表面能项.

为什么关闭状态没有表面张力能？因为关闭时结合比较紧，不能被拉开.

提示

其实一种理解是这并不是完全的一个二能级，因为受到了表面张力能的调控；但是另一种理解是 eβτΔAe^{\beta\tau\Delta A} 是一个概率性质的因子，表征 open 态出现的概率.

打开概率：

p0=eβτAeβτA+e−β(εc−εo)p_0=\frac{e^{\beta\tau A}}{e^{\beta\tau A}+e^{-\beta(\varepsilon_{\text{c}}-\varepsilon_{\text{o}})}}

这是一个随着 AA 陡峭变化的函数. 简单的图像理解：closed 态和 open 态都是自由能极小值点，在没有施加力的作用时，closed 态的能量更加低；而施加力之后，open 态的能量降低了.

这被称为 allostery (别构效应)：生物体希望在生产出蛋白质之后能够调控这种蛋白质的工作，比如，

一种蛋白质用来结合葡萄糖，它结合的位点在一个「夹子」的中间；一开始蛋白质的「夹子」是打开的，结合葡萄糖的亲和力很低. 但是引入一个调控因子 X，结合蛋白质的另一个位点，改变蛋白质的构象把这个「夹子」关上，那么蛋白质和葡萄糖就能紧密结合.

别构效应是产生在蛋白质两个不同位点之间的调控效应.

别构效应也需要满足一定的热力学规律. 认为反应物和调控因子分别是 GG 和 XX，平衡态先结合哪一个都有可能，但是

ΔGG→GX−ΔG0→X=ΔGX→GX−ΔG0→G\Delta G_{G\to GX}-\Delta G_{0\to X}=\Delta G_{X\to GX}-\Delta G_{0\to G}

也就是，先结合 XX 会造成 GG 的结合概率增大；反之，先结合 GG 会对 XX 的结合产生同样的效果，所以不管是怎么结合，反应都朝着我们期望的方向「GXGX 均结合」加速进行，产生了互相影响的效果.

这个调控效应在生物中极为常见，我们常说的活化效应其实也是同一个机制.

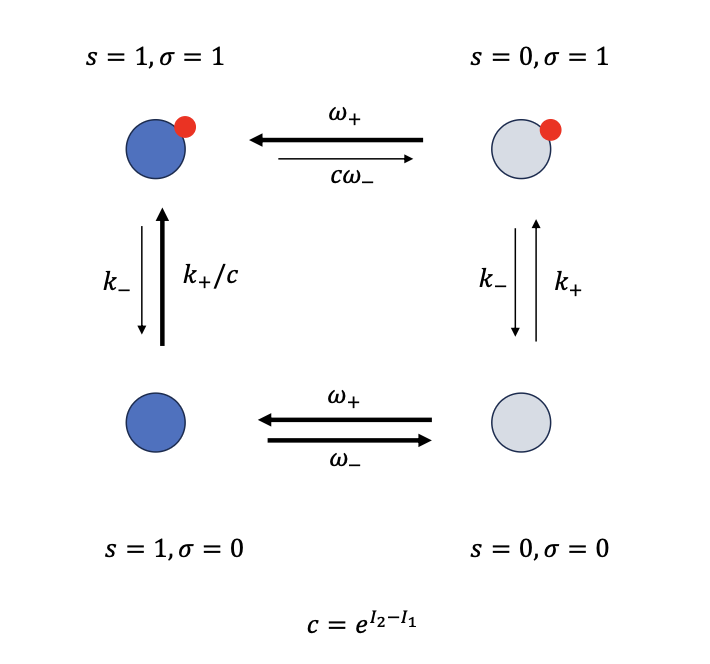
下图 σ\sigma 表示是否活化、ss 表示是否与反应物结合：

更进一步，我们有所谓「协同」(Cooperativoty)，比如某种抑制因子结合一个蛋白后，对近邻的一个蛋白亲和力的影响. 这其实很类似于 Ising Model，也是磁矩近邻之间产生相互作用.

这时候，配分函数写成：

Z=1+2e−β(ε−μ)+e−β(2ε+J−2μ)Z=1+2e^{-\beta(\varepsilon-\mu)}+e^{-\beta(2\varepsilon+J-2\mu)}

其中 JJ 体现了两个近邻单元的相互作用，这是血红蛋白结合氧气的一个理论建模，在上世纪 60 年代就已经完成. 计算得到一个很复杂的式子

⟨N⟩=2(c/c0)e−βΔε+2(c/c0⋅e−βΔε)2e−βJ1+2(c/c0)e−βΔε+(c/c0⋅e−βΔε)2e−βJ\braket{N} = \frac{2(c/c_0)e^{-\beta\Delta\varepsilon}+2(c/c_0\cdot e^{-\beta\Delta\varepsilon})^2e^{-\beta J}}{1+2(c/c_0)e^{-\beta\Delta\varepsilon}+(c/c_0\cdot e^{-\beta\Delta\varepsilon})^2e^{-\beta J}}

出现 cc (浓度因子) 是因为化学势中间含有这个.

如果 J=0J=0 (无相互作用)，上面的式子简化为

⟨N⟩=2(c/c0)e−βΔε1+(c/c0)e−βΔε=2⟨N0⟩\braket{N}=2\frac{(c/c_0)e^{-\beta\Delta\varepsilon}}{1+(c/c_0)e^{-\beta\Delta\varepsilon}}=2\braket{N_0}

这就是两个 N0N_0 相加罢了，没有体现相互作用的效果.

Monod-Wyman-Changeux (MWC) model：如果 subunits 之间的相互作用足够强，那么所有蛋白质的构象是完全一致的，只能同时活化或者同时失活，呈现强关联的特征.

/Example/

乙酰胆碱，一种小分子神经递质. 乙酰胆碱的受体是一种五聚物，有两个结合位点，只要结合了一个位点就能够打开让 Na+\text{Na}^+ 进入，所以一共有八个状态：左边、右边结合或不结合 (2×2=42\times2=4 个状态) 和活化后的 44 种结合状态，可以分别计算能量和概率.

但是这里有简并的存在！对于左边结合一个和右边结合一个的态，自由能是一样的，所以计算配分函数时这一项多一个 22 的因子.

一般地，对于 MWC Model，

Fclosed(1)=Fc−ΔFc−μ=Fc−kBTln⁡cKclosedFopen(1)=Fo−kBTln⁡cKopen\begin{aligned} F_{\text{closed}}(1) &= F_{\text{c}} -\Delta F_{\text{c}}-\mu = F_{\text{c}}-k_BT\ln\frac{c}{K_{\text{closed}}}\\\\ F_{\text{open}}(1) &= F_{\text{o}}-k_BT\ln\frac{c}{K_{\text{open}}} \end{aligned}

假设有 nn 个结合位点，所有结合位点都强关联 (结合一个就全部响应)，那么

Zo=e−Fo/kBT(1+c/Ko)n ,Zc=e−Fc/kBT(1+c/Kc)nZ_{\text{o}}= e^{-F_{\text{o}}/k_BT}(1+c/K_{\text{o}})^n\,,\quad Z_{\text{c}}=e^{-F_{\text{c}}/k_BT}(1+c/K_{\text{c}})^n

于是

po=ZoZo+Zc=LL+(1+c/Kc1+c/Ko)n ,L=e−β(Fo−Fc)p_{\text{o}}=\frac{Z_{\text{o}}}{Z_{\text{o}}+Z_{\text{c}}}= \frac{L}{L+(\frac{1+c/K_{\text{c}}}{1+c/K_{\text{o}}})^n}\,,\quad L=e^{-\beta(F_{\text{o}}-F_{\text{c}})}

我们考虑结合非常困难的情况，这时 Ko≪c≪KcK_{\text{o}}\ll c\ll K_{\text{c}}，上述函数化为一个 Hill 函数，

po≈(1+c/Ko)n(1+c/Ko)n+1/Lp_{\text{o}}\approx\frac{(1+c/K_{\text{o}})^n}{(1+c/K_{\text{o}})^n+1/L}

nn 变大时，这个函数的响应越来越灵敏，所以很适合用在神经系统的感受器上. 这个模型非常有趣，因为它体现了蛋白质之间的相互关联竟然能影响系统对外部刺激的响应模式. 这个策略是平衡态所能达到最强的响应方式了，当然我们后面会说非平衡态会得到更加好的响应模式.

下面我们说动力学校对 (Kinetic Proofreading)，也就是蛋白质正确折叠的机制.

注意

很恐怖的一点是，这是 Hopfield 发现的，没错，就是那个去年因为神经网络获得 Nobel Prize for Physics 的 Hopfield.

这个机制具体而言是，蛋白质的错误折叠有更大的概率被解离，而且直接被解离到初始的状态上.

原文：Kinetic Proofreading: A New Mechanism for Reducing Errors in Biosynthetic Processes Requiring High Specificity, Proc. Nat. Acad. Sci. USA Vol. 71, No. 10, pp. 4135-4139, October 1974

更新日志

2026/9/9 05:47
查看所有更新日志
  • d6df0-build(theme): theme update于
  • c3099-build(theme): update theme于
  • 79171-feat(note): add biophysics note于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)