外观
Lesson 12 Time Series Analysis
约 3263 字大约 11 分钟
2025-12-04
提示
Quizzes
什么是 truncated data?举个例子.
截断的数据,比如探测器只能探测流量在某个阈值之上的源.
实际上我们不知道阈值之下到底丢了哪些数据、丢了什么数据.
什么是 censored data?举个例子.
模糊的数据,比如探测器在某一个波段看到了某个源,但是另一个波段看不到这一个源.
实际上我们知道那里有一个源,而且我们知道它在某个波段高于阈值.
下面关于 flux-limited 样本的表述,正确的是:
- 更亮的源所占比例被高估了
- 总有一个表观的趋势 —— 更大的距离对应着更大的光度
- 表观的趋势一定是 biased.
- 如果两个本征的量是相互独立的,那么表观的量也相互独立.
选择 a., b..
如果不考虑测量误差,密度均匀分布,那么 flux function 和光度分布完全无关,我们的阈值只是在这个 function 上做截断,不会影响 flux function 的具体形式,因此 c. 是对的.
什么是 flux-limited samples 的 Eddington bias?
有几个条件:
- 暗的源比亮的源多很多
- 测量误差存在,而且是随机分布的
这种情况下暗的源可能因为误差而被测成亮的源,反之亦然,我们会高估暗源数量.
什么是 volume-limited data?
……
……
倒数第二节课了.
时间序列指的是,我们测量一个数据随着时间的变化,
(t1,y1),(t2,y2),(t3,y3),⋯
测量时间序列的目的就是找到某个变量随着时间的变化,想要了解这个变化关系;同时来预测后面的可能值和可能事件.
比如恒星的光变曲线,可以预测后面的某个时间的恒星的光度是什么样的;或者统计 γ 射线暴在全宇宙的分布,预测这种事件出现的频率.
而且实际上时间序列并不一定要有「时间」,只要是一种二维的、两者呈现函数关系的统计分布,都可以叫做时序分析.
有几种很典型的时序数据 (狭义上的):
- Periodic:天鹅座 RR 变星,周期性的光变曲线
- Burst:行星对后面的恒星产生微引力透镜,光稍微变亮一点点;或者是某种爆发事件.
- Chirp (啁啾):频率会变化的周期性结构,比如双黑洞合并的引力波事件,两者越靠近频率越高.
但是宇宙并没有上面这些数据一样 nice,比如这样的数据:
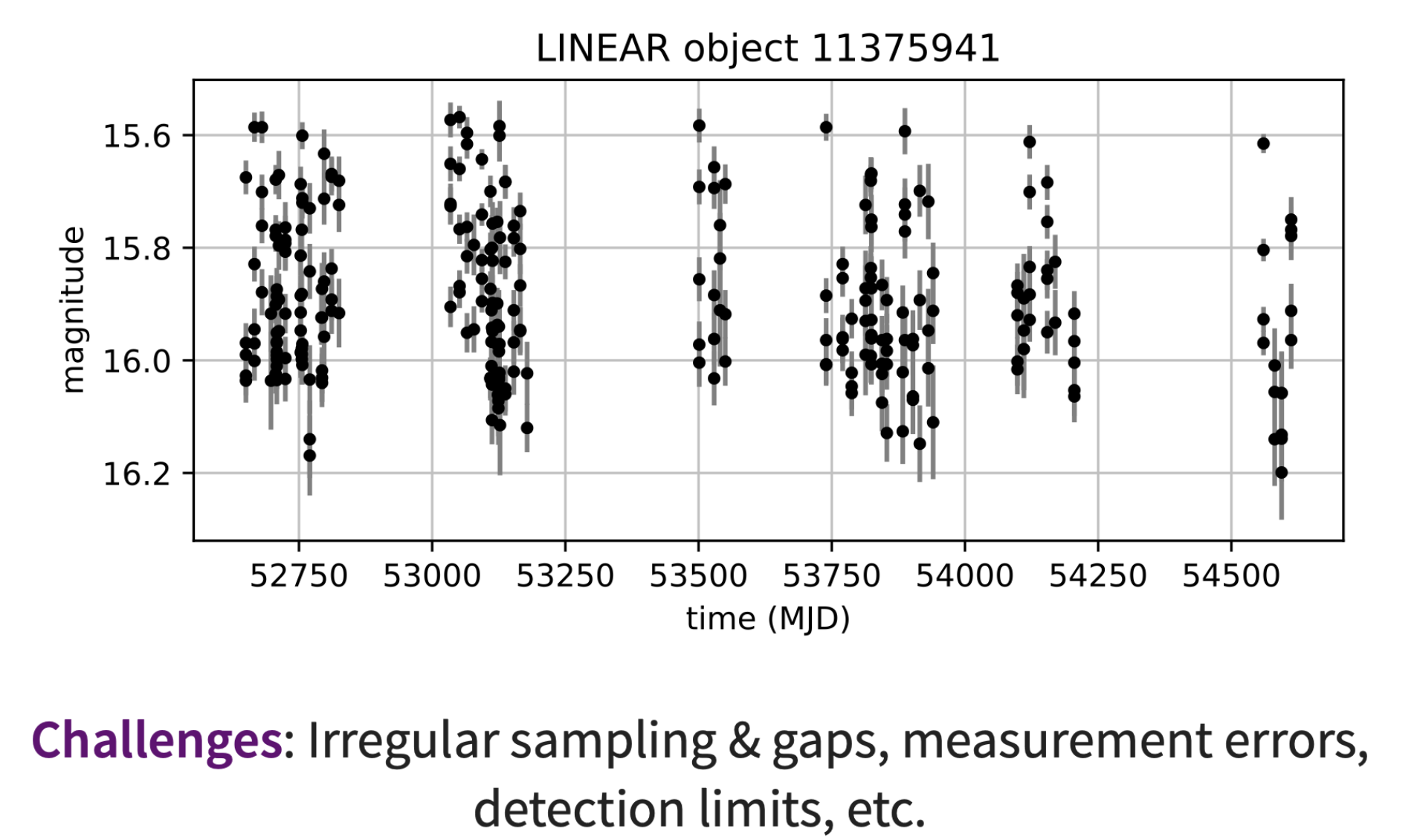
实际上这一坨是非常好的数据,虽然误差很大、被阈值所限制,但是我们经过一些分析会得到一颗极好的变星.
Fourier Analysis
「Let frequencies tell the story of time.」
先来看公式:
H(f)=∫−∞∞h(t)e−2πiftdt,h(t)=∫−∞∞H(f)e2πiftdf
和我们在 Lesson 8 中遇到的类似,用一组基函数来组合出未知的某个函数,这里的基函数恰好是三角函数.
几种常见的 Fourier 变换:
- 三角函数的变换是 δ 函数
- Gauss 函数的变换是另一个 Gauss 函数
- 方波变换为 sinx/x 形式的函数
- 脉冲变换为新的脉冲
/Example/
分析
2sint+sin3t
在复平面上,表现为一个以 2 为半径的圆周上面有一个以 1 为半径的小圆在旋转 (这不就是 3b1b 的科普演示视频吗),类似本轮与均轮.
按照这个思路,我们可以分解 RR-Lyrae 的光变曲线,分解到 8 个 mode 上就几乎可以完全拟合.
换句话说,古人的本轮和均轮在描述行星轨道上的成功实际上并不是因为行星的轨道多么的好,而是这样分解本来就能够把任意的周期轨道拟合清楚.
另外,Fourier 变换提供了一个高速计算卷积的方法. 卷积指的是:
(f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ
一般而言,误差和真实值实际上就是一种卷积,我们要做的大多数时候是反卷积,也就是上述计算的逆运算. 一个定理是,
F(f∗g)=F(f)⋅F(g)
也就是卷积的 Fourier 变换等于两个函数各自的 Fourier 变换之积.
在时域上,我们可能有一个非常剧烈的抖动数据,这时候用一个窗口函数 (方波脉冲) 和这个数据做卷积,就得到一个更平滑的数据曲线 (这也是 KDE 的原理).
而同时在 Fourier 空间中,这个操作要更加容易,就是把原始数据的变换和窗口函数的变换乘在一起而已,再变换回去得到光滑的数据曲线.
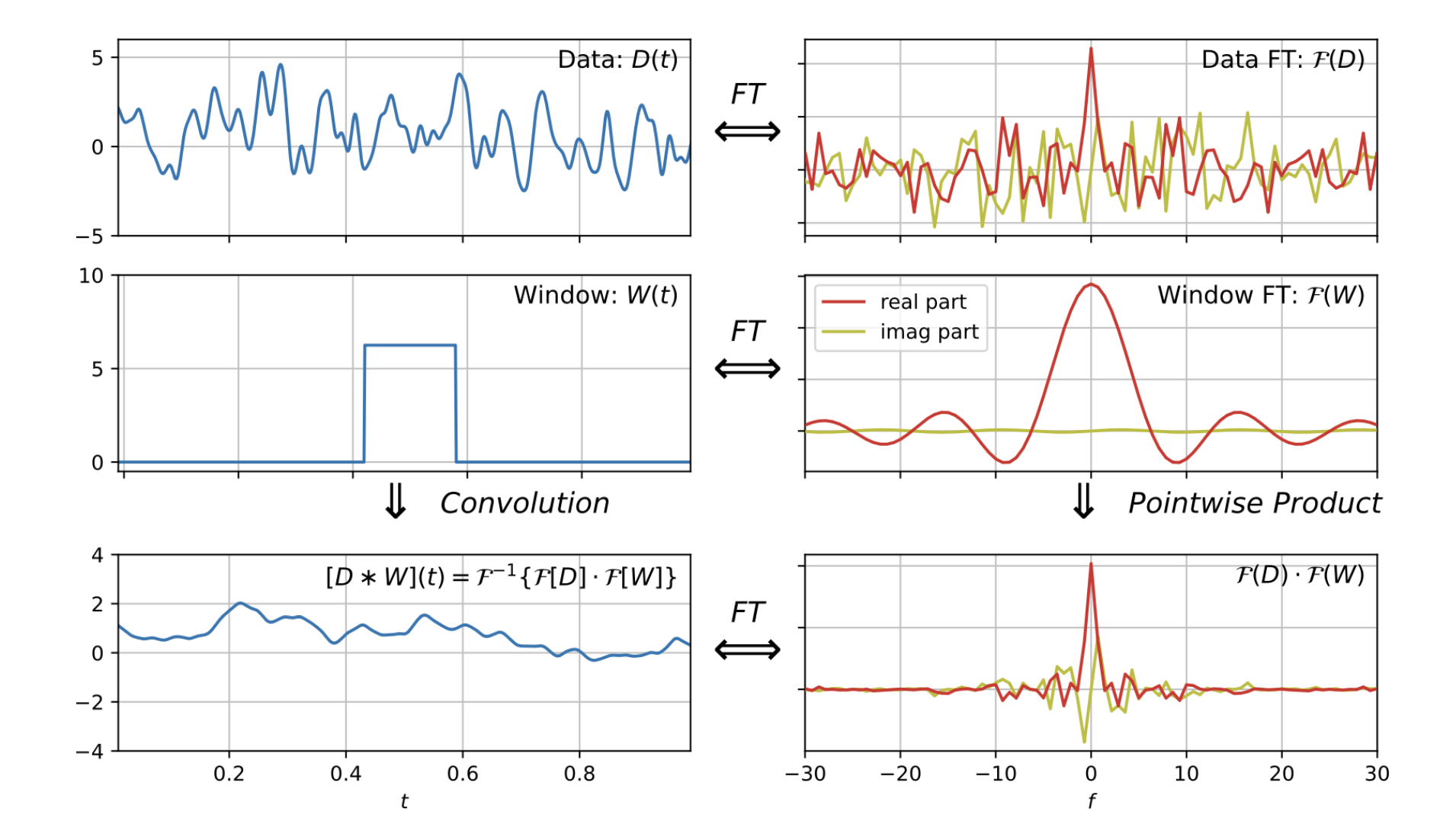
DFT (Discrete Fourier Transform, 离散 Fourier 变换):在时间尺度上均匀采样,原来的积分化为求和:
Hk=j=0∑N−1hje−2πift/N
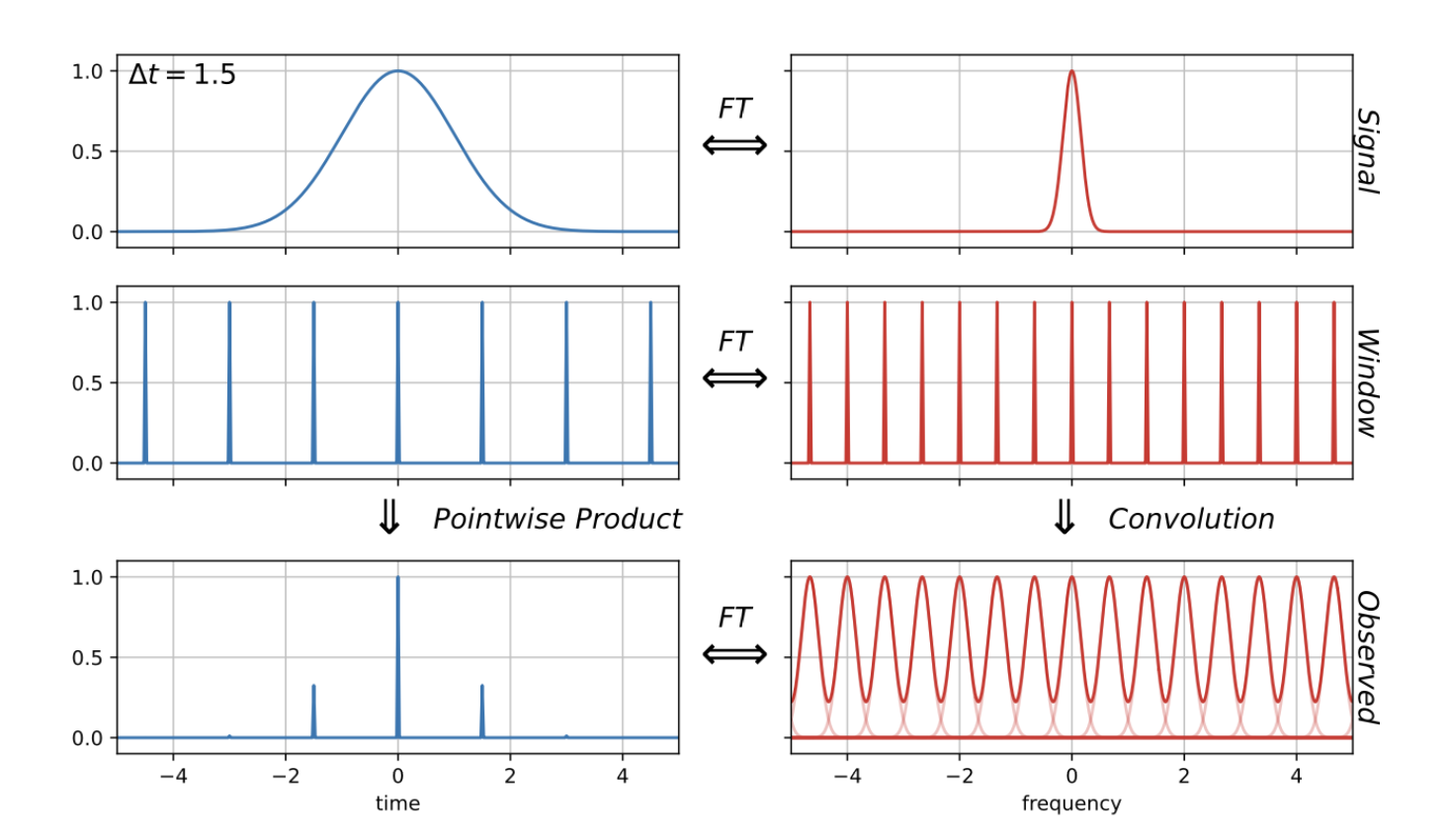
在时域上,用一个等间隔的 δ 函数去对任意一个目标函数去采样,那么这个操作相当于时域上的乘积,在 Fourier 空间是一个卷积,采样函数变换还是一个 δ 函数序列,原来的函数的变换作用到这个 Fourier 空间的采样函数上就相当于一个 KDE,相当于把这个函数复制了很多遍.
当采样的时间间隔很小时,Fourier 空间的采样函数间隔很宽,可以完美的把被复制的函数拆开,然后完全复原原函数;但是如果时间间隔很大,Fourier 空间的采样函数间隔很窄,会把复制的多份目标函数的 Fourier 变换重合在一起,无法分辨,就没办法完美还原.
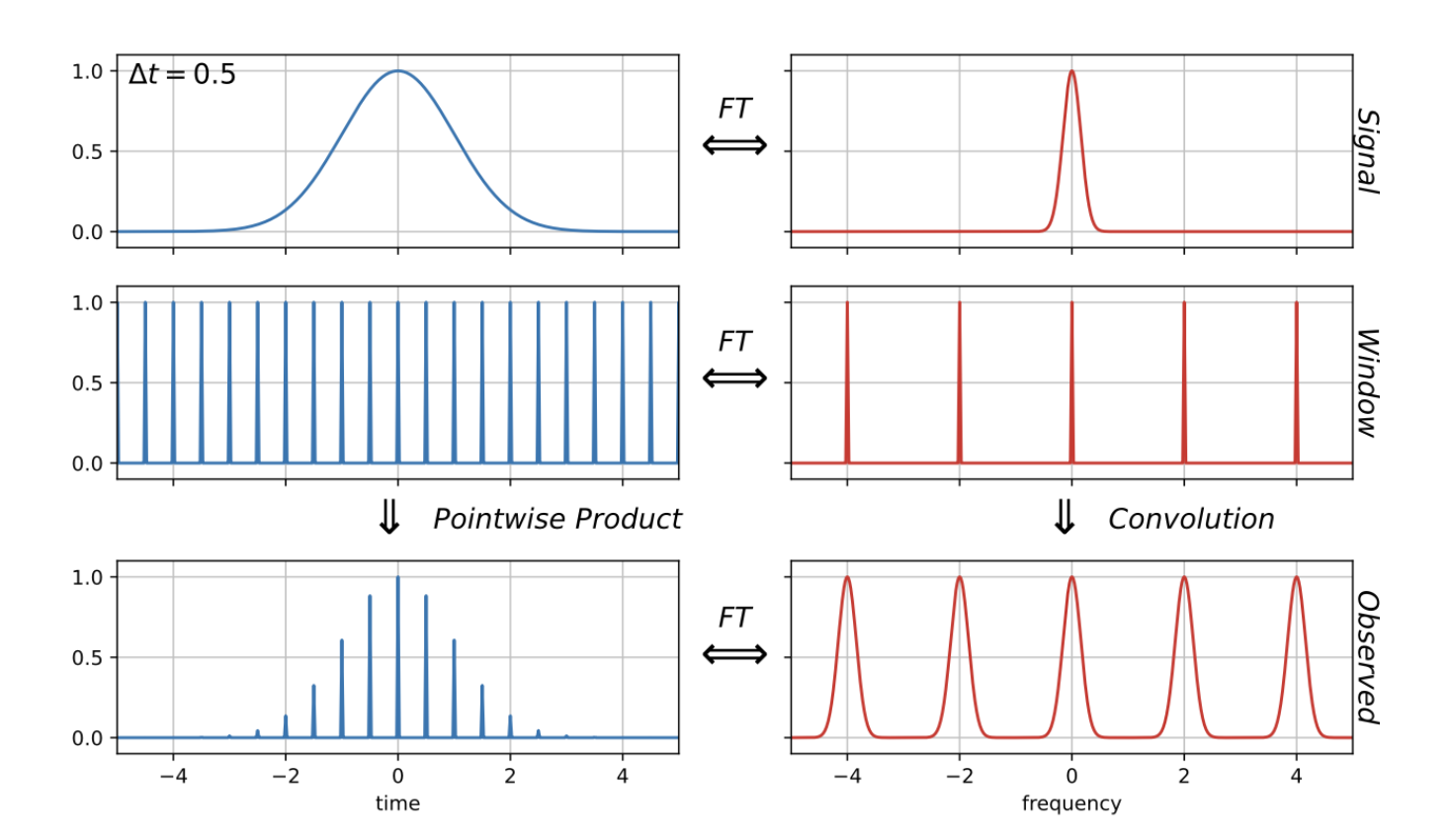
FFT (Fast Fourier Transform, 快速 Fourier 变换):这个算法的复杂度是 O(NlogN).
The most important numerical algorithm of our lifetime.
—— Gilbert Strang
在代码上调用很简单:
import numpy as np
t, y = generate_data(...)
f = np.fft.fftfreq(t.size, t[1] - t[0])
y_fft = np.fft.fft(y)
# Only non-negative frequencies are needed for real-valued data
sel_freq = (f >= 0)
psd = np.abs(y_fft[sel_freq])**2 # power spectrumPeriodic Time Series
我们在第八次作业已经被模型选择所折磨过,那里用不同的 kernel、换不同模型都会对结果影响很大,而且效果也并不好. 同时,这些数据做 DFT 也不行,因为我们不一定是在时间上均匀采样的. 所以我们引入一个新的东西:periodogram (周期图)
对于一个光变曲线:
R(f)=j=1∑Nyjcos(2πftj),I(f)=j=1∑Nyjsin(2πftj)
周期图为
PS(f)=NV2[R2(f)+I2(f)]
相当于做完离散 Fourier 变换之后,把模提取出来. 得到的效果很好,但是缺点在于我们需要很密的采样.
但是如果我们随机地采样,而不是周期性地采样,并采用改进的周期图 Lomb-Scargle Periodogram:
τi(f)≡ti−4πf1arctanj=1∑Ncos(4πftj)j=1∑Nsin(4πftj)C(f;τj)=j=1∑∞cos2(2πfτj),S(f;τj)=j=1∑∞sin2(2πfτj)PLS(f)=V1[C(f;τj)R2(f;τj)+S(f;τj)I2(f;τj)]
在 30 个周期内仅仅采样 20 个点,也能得到在真实频率处的一个尖锐的峰值.
这说明大自然给了我们一个机会,随机地采样点比周期性但是频率低的采样点能够更高效地确定周期性数据的频率.
实际上,周期图的高度表征了后验比,所以真实频率给出的高度会是指数上升的,决定效率相当高. 另外,加权周期图对应我们在之前的课程中讲到的 χ2 分布.
LS 周期图的代码调用:
from astropy.timeseries import LombScargle
ls = LombScargle(t, y) # or with errors: LombScargle(t, y, dy)
frequency, power = ls.autopower(
minimum_frequency=0.01, maximum_frequency=10
)参考文章:Jaynes 1987
Localized & Stochastic Signals
对于 burst 或者 chirp 之类形态的信号,我们的真实数据是局域性的,这时候 Fourier 变换效果不好,因为没有周期. 我们引入又一个新的概念:spectrogram (谱图),相当于套了一个时间窗口之后的 Fourier 变换,对于 chirp 信号非常合适 (但是相对应地,对于 burst 信号效果不好).
这个方法是 2016 年第一次引力波探测所使用的方法.
小波 Fourier 变换:
Hw(t0;f0,Q)=∫−∞∞h(t)w(t;t0,f0,Q)dt
其中的 kernel 是
w(t;t0,f0,Q)=Q1e2πif0(t−t0)exp[−Q2f0(t−t0)2]
可以同时给出频率和时间的信息. 用小波变换可以给出广义的 spectrogram,时间窗口是可变的而不是固定的,小波功率谱同时表达了时间和频率,同时筛选效率极高.
代码调用:
from astroML.fouier import wavelet_PSD
f0 = np.linspace(0.01, 1, 100)
WPSD = wavelet_PSD(t, y, f0, Q=1.0)最后我们来说一种完全随机的信号,不属于上面几种,大致上是「有一段时间内两个量有强关联,另一段时间内两个量没有关联」,比如 AGN (活动星系核),在活跃期吸积了一大块物质,呈现明显的时间关联光变曲线;宁静期没有物质吸积,光度不出现明显变化.
引入相关函数:
CF(τ)=σfσg1T→∞lim∫(T)f(t)g(t+τ)dt
更狭义地,有自相关函数:
ACF(τ)=σf21T→∞lim∫(T)f(t)f(t+τ)dt
自相关函数在 0 处值为 1,如果出现白噪声,那么就是一个完全的 δ 函数.
/Example/
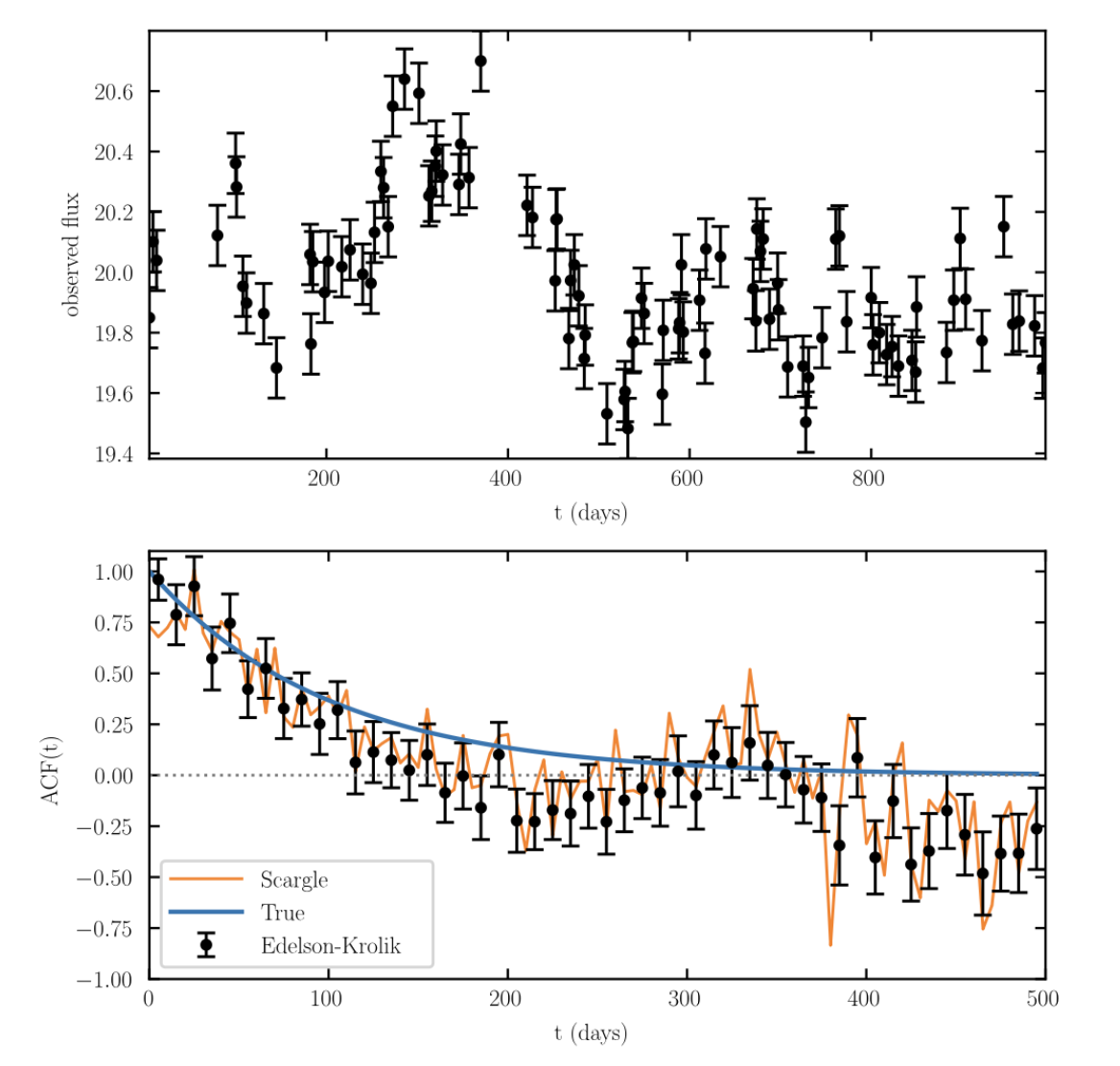
随机行走,时间越长关联性越差,给一个 e−λt 的衰减数据模拟.
如图:
Exercise: Light Curve Periodicity
在说今天的练习之前,先说一下大作业.
课程给了 5 个预设的问题,当然也可以说服自己的队友来做一些新的问题. 我们给出的问题在上限上是可以发表的成果.
Hubble Diagram
查看题目中给出的文章,在 GitHub 中有现成的数据,利用文章中的模型来拟合,然后和文章中的结果相比较.
如果要做得更深入:可能在模型中有些东西人们并没有考虑到. 比如拟合的数据会存在残差,如果两类不同超新星的残差很不一样,那么意味着前人做的结果很多是错的,因为他们没有考虑这两种不同超新星在定标的时候产生的效果不同.
这甚至可以完全推翻现有的宇宙学结果.
Selection of High-Redshift Galaxies
训练集中有已经知道红移的星系,然后利用训练集训练神经网络,确认新星系的红移,这是典型的 classification.
Photometric Redshifts of Galaxies
用 DESI 的数据来做训练集,复现题目中论文的结果.
TESS Transient Detection
从 TESS 的数据 (这完全是一个宝库!) 中寻找新的变星,做 clustering 找到一些比较特殊的变星,分析是不是有和之前的种类不一样的变星;甚至可以和 Gaia 的数据做对比.
Radom Catalog for 2PCF
这是下一节课要讲的东西,用随机样本来处理红移的数据.
目前业界的方法是直接生成变量,但是这个方法是有缺陷的.
12.25 口头报告,1.15 书面报告. 评分规则:
Oral presentation (group): 25%
- 15th week (Dec 25, 2025)
- 20 minutes presentation + 5 minutes Q&A
- 1% bonus per persentation for asking effective questions
Written report (individual): 25%
- Due date: Jan 15, 2026
- PDF report + code submission
- 5% bonus for English write-up
警告
似乎没时间做今天的练习了...
这一次复现第八次作业,用周期图来重新完成之前的 UltraNest 和 KDE 做的结果,然后发现周期图在这个 case 上远强于 UltraNest. 缺陷在于,我们今天的方法只能做二维.
下次课请鹏城实验室的一位助理研究员来做 AI for Physics 的讲座,再下一次才讲最后一节课的内容.
更新日志
2025/12/4 15:35
查看所有更新日志
b7b8f-feat(note): add as note于