外观
Lesson 9 Density Estimation
约 2734 字大约 9 分钟
2025-11-13
提示
Quizzes
在不同情况下应该怎么做推断?
我们已经了解得很深入.
参数推断
有一定了解.
模型选择
完全不了解.
非参数统计
比如,用基函数展开可能的函数形式.
在参数推断时,最关键的是哪一个量?
后验,也就是:
P(θ∣DMI)=P(D∣MI)P(D∣θMI)P(θ∣MI)
在模型选择时,最关键的是什么?
Bayes 因子,也就是后验比,其中的重要成分是我们所谓的归一化因子 —— 证据.
下面有关非参数统计的表述,正确的是:
- 没有参数
- 参数的数量固定
- 利用一个 flexible 函数形式,来保证能够符合我们的模型
- 设置弱的、general 的先验 (not necessarily uniform)
- 通常用更多参数,而不是用参数化的模型
- 最终我们可以得到一些性质,以便于进行下一步的参数化模型选择
选择 c., d., e., f.
基函数展开有关表述:
- 结果会取决于基函数
- 基函数的性质如果出现了简并,那么最后的结果不能用
- 不同问题需要选取不同基函数
- 基函数的类型、项的数量可以在下一步被模型选择所精确
选择 b., c., d.
Gaussian 过程有关表述:
- 描述的不是函数的分布
- 先验是由一个平均函数 (often zero) 和一个有超参数的协方差核所决定的
- 超参数可以从训练集得出
- 如果训练集距离真值很远,我们不能得到好的预测
- 如果数据有噪声,那么不能工作
- 如果数据不是 Gaussian 过程生成的,那么不能得到正确的结果
注意
Gaussian 过程的具体含义是,我们利用不同的协方差矩阵,在函数空间对函数进行采样 (超参数的采样). 训练集的作用是,告诉我们这些采样的函数的极限范围大概是多少、弥散大概是怎样的.
选择 a., b., c.
我们用什么来描述「不确定的程度」?
信息熵:
H=−i∑pilnpi
无差别原理是我们最早提出的、判断未知事件的概率分布的原理,它和熵有何关系?
无差别原理对应最大熵原理.
Gauss 分布和最大熵原理的关系?
给定均值和方差的情况下,最大熵对应的分布是 Gauss 分布.
上节课我们做的是非参数统计,完全不知道如何构建模型. 这节课我们的了解更少,只能从数据本身推断出可能的结构,甚至无法取基函数.
我们的目的是:
- 从很多噪声的 MCMC 采样中得到 smooth, bin-free 的概率分布
- 没有事先模型、解析结果的情况下,得到一个估计
这个过程可以在真实的物理上,也可以是对一个虚拟的参数做估计.
Histograms
直方图的定义是,
h(x)=k=1∑MhkΠ(x;xk−1,xk)
实际上就是一种数数,但是很有用,比如我们做数值积分就可以利用直方图做 Riemann 和.
直方图 bins 太少,会导致很多重要的数据特征没有体现出来;bins 太多,会产生大量的「毛刺」,噪声非常明显. 我们在取 bins 的时候,有一个 Scott 经验法则,对于 N 点和标准差 σ^,取
vscott=3.49σ^N−1/3
但是仅仅对 Gauss 分布有效. 一个简单的拓展是,Freedman - Diaconis rule,把对长尾敏感的标准差换成百分位数,得到
vFD=2(q75−q25)N−1/3
这些经验法则并不能很好地处理窄峰、比较精细的分布 (比如课堂上的 5 个 Lorentz 分布叠加的神必分布),我们还需要更加有效的方法.
Knuth Method
暂时先不考虑每个 bin 的宽度不同. 考虑 M 个 bin,M 作为参数,就变为我们熟悉的问题了,即对下面这个函数做参数估计:
h(x)=VMk=1∑MπkΠ(x;xk−1,xk),k=1∑Mπk=1
就是要找到一个 M 使得 h(x) 最接近我们的数据. Bayes 定理:
P(π,M∣DI)∝P(D∣π,MI)P(π,M∣I)=P(D∣π,MI)P(π∣MI)P(M∣I)
边缘化为
P(M∣DI)=∫P(π,M∣DI)dπ∝P(M∣I)∫P(D∣π,MI)P(π∣MI)dπ
先验是均匀分布的 M,以及多方的 Jeffreys' for π:
P(π∣MI)=ΓM(1/2)Γ(M/2)k=1∏Mπk−1/2
似然是
P(D∣π,MI)=(VM)Nk=1∏Mπknk
虽然结果并没有比 FD-rule 好很多,但是至少已经抛弃了 Gauss 分布的前提.
Adaptive binning: Bayesian Blocks
直译过来就是自适应的 bin 宽度. 这种方式能够处理小的尖峰 (这个方法是由研究脉冲的天文学家提出的),在不同的数据密度处取不同的 bin 宽度.
这一次我们联合优化 bins 的数量 Nb 和 bins 的宽度构成的向量 T. 这种情况我们不得不做假设了,下面说几种.
假设数据由 Poisson 分布生成,那么
lnLmax=k=1∑NblnLmax(k)=k=1∑Nbnk(lnnk−lnTk)+const.
第二种假设是考虑仪器的测量误差是 Gaussian 分布的,有
lnL({xi,σi}∣Nn,TI)=−21k=1∑Nbi∈k∑(σixi−μk)2+const.
这个方法的问题在于,如果我们移动 bin 的起始点位置,会对最后的记过造成很大的影响;另外,高维情况下几乎没有办法处理. 代码:
import numpy as np
import matplotlib.pyplot as plt
from astropy.visualization import hist
from scipy.stats import norm, laplace
# Generate sample data
N = 500 # total number of samples
weights = [0.7, 0.15, 0.15] # mixture weights
dists = [laplace(0,0.4), norm(-4,0.2), norm(4,0.2)]
data = np.hstack([d.rvs(int(N * w)) for d,w in zip(dists,weights)])
fig, ax = plt.subplots()
hist_values, hist_bin_edges = [], []
for method in ['scott', 'freedman', 'knuth', 'blocks']:
value, edges, _ = hist(data, bins=method, ax=ax, density=True)
hist_values.append(value) # retrieve histogram values
hist_bin_edges.append(edges) # retrieve bin edgesContinuous Estimators
Kernel Density Estimator (KDE)
在每个样本附近放一个小的 bump,bump 的求和会给出一个光滑的概率密度分布 (bump 是光滑的). 得到
f^h(x)=NhD1i=1∑NK(hd(x,xi))
其中 K(x) 是 kernel,也就是每一个 bump 的形状. 和 histogram 对比,可以看出 KDE 的好处是,可以得到连续的分布. 但是最大的缺点是,整个分布对带宽 (kernel 的宽度) 非常敏感,不同带宽会得到完全不一样的分布.
这本质上和 bins 的数量问题是一样的,也有 Scott's rule 和 FD rule. 还有一个 cross - validation 方法:最大化下面的 leave - one - out (LOO) 的 log - likelihood:
CVLL(h)=N1i=1∑Nlogf^hi−i(xi)
KDE 的另一个好处是,可以方便地给出测量的误差. 我们先假设 f(x) (分布) 是测量误差和真实分布的卷积:
f(x)=(h⋆g)(x)≡∫h(u)g(x−u)du
仔细观察其实也可以发现,KDE 给出的本来就是 kernel 函数和真实分布的卷积,所以做一个反卷积会得到我们所谓的真值分布.
在高维情况下,带宽是一个矩阵,这时需要对数据做一个 pre - whitening (清洗),将每个维度的参数无量纲化,变成一个对称矩阵,用一个各向同性的 kernel 去做 KDE. 代码:
import numpy as np
from sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV, LeaveOneOut
param_grid = {'bandwidth': np.logspace(-1, 1, 20)}
kde = GridSearchCV(KernelDensity(kernel='gaussian'),
param_grid, cv=LeaveOneOut())
kde.fit(data[:, None])
print("Best bandwidth: ", kde.best_estimator_.bandwidth)
# Evaluate the density on a grid of points (`x_grid`)
pdf_kde = np.exp(kde.best_estimator_.score_samples(
x_grid[:, None]))
# Or, if you have a fixed bandwidth
# kde_fixed = KernelDensity(bandwidth=0.5, kernel='gaussian')
# kde_fixed.fit(data[:, None])k - nearest neighbor (k - NN) estimator
基于「邻居」的 kernel:
f^k(x)=NVD(dk)k
也就是自适应的一种 kernel,不是全部一样的 kernel. 这里 VD(dk) 是 D 维、直径 dk 的球的体积. 虽然比之前的 KDE 要更进一步,但是还是有一个自由参数,也就是 k —— 到底要取几个「邻居」?
代码实践仍然不算难,调用 astroML 包 (astro - machine learning),
import numpy as np
from astroML.density_estimation import KNeighborsDensity
from sklearn.model_selection import GridSearchCV, KFold
def knn_scorer(estimator, x_data, y=None):
"""Custom scorer for k-NN density estimator"""
dens = np.maximum(estimator.eval(x_data), 1e-99)
return np.mean(np.log(dens))
param_grid = {'k': np.arange(5, 125, 5)}
knn = GridSearchCV(KNeighborsDensity('bayesian'),
param_grid, cv=KFold(n_splits=5), scoring=knn_scorer)
knn.fit(data[:, None])
print("Best k: ", knn.best_estimator_.k)
# Evaluate the density on a grid of points (`x_grid`)
pdf_knn = knn.best_estimator_.eval(x_grid[:, None])AI - Based Directions
注意
大家是不是写作业的时候离不开 AI 了...
神经网络的不同权重可以表达处不同的函数. 两种手段:
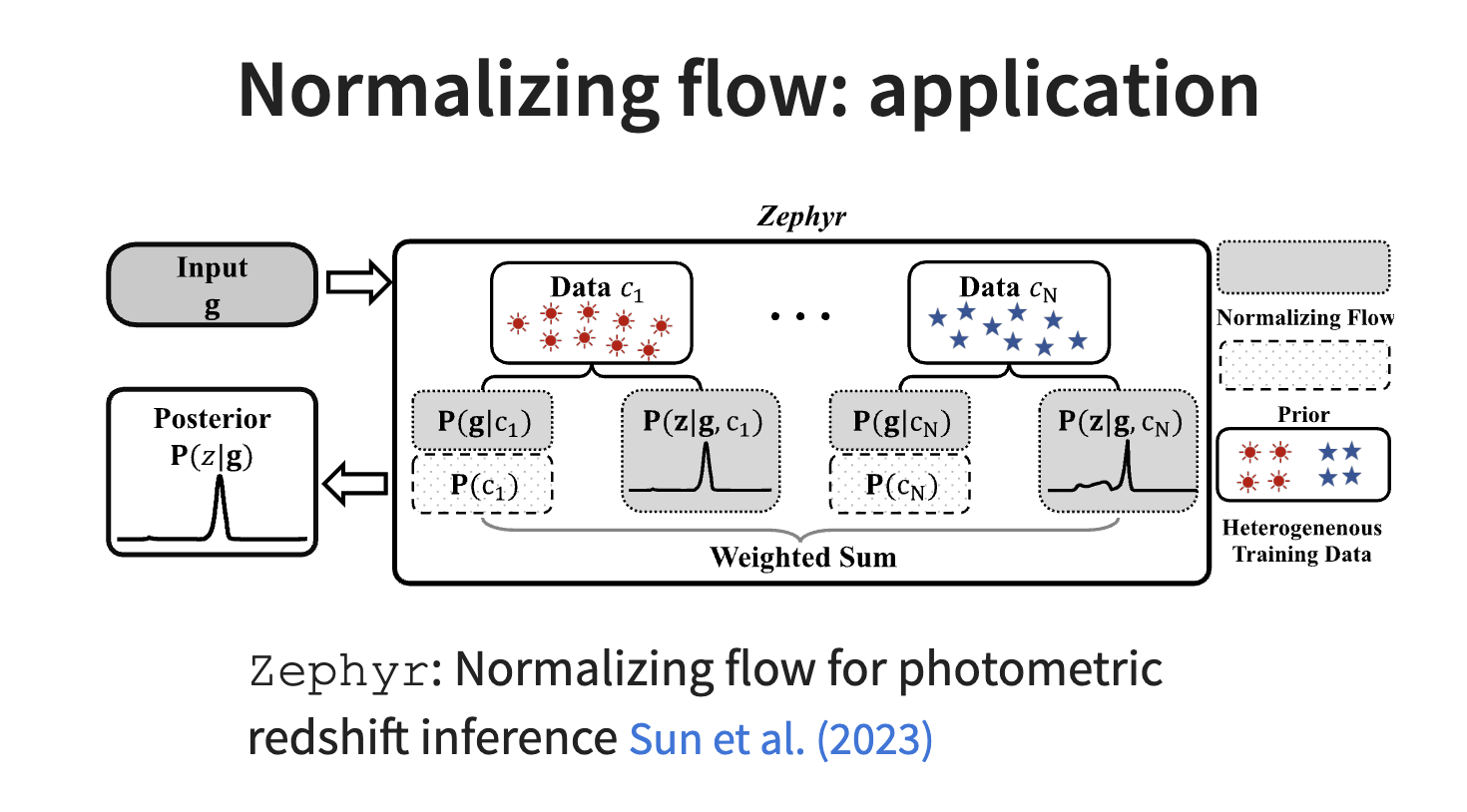
- Normalizing flows:从一个简单的基础分布 (比如说 Gaussian) 开始,学习一个可逆双射,映射进入数据空间;从这些变量的变化中找到 density.
- Autoregressive models:通过乘积法则把联合分布因式分解,用神经网络把每一个条件概率算出来.
Normalizing Flows:
从一个简单的分布开始,z0∼N(0,1),考虑一个序列 zk=fk(zk−1),通过这样的序列把标准的正态分布变成一个任意的分布:
pX(x)=pZ(z0)i=1∏K∣detJfi(zi−1)∣−1
这里,Jfi 是 Jacobian Jfi(zi−1)=∂fi(zi−1)/∂zi−1. 我们训练集的目的是最大化似然:
θmaxN1j=1∑NlogpX(xj;θ)
Autoregressive Model:
利用神经网络来对序列中的每一个步骤建模,其实就是一个乘积法则:
P(x1,x2,⋯,xD)=i=1∏DP(xi∣x1,x2,⋯,xi−1)
下面我们可以做一件更更加有野心的事情,我们可以不知道似然是什么样子了,但是给定参数、模型和背景信息可以模拟出整个数据. 也就是,可以学习后验,来模拟出似然,得到后验;或者学习似然,模拟出后验.
计算参数和数据的联合分布,P(θ,x),神经网络学习这样的分布之后,可以在输入观测数据 x 之后直接输出参数的后验分布.
Exercise
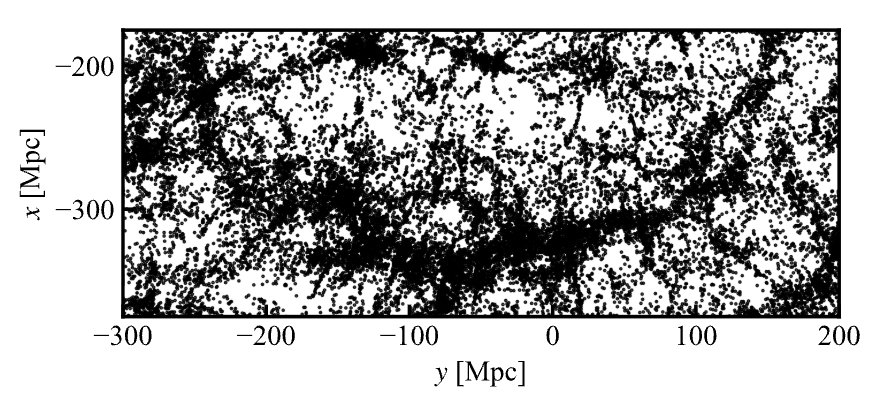
SDSS 巡天的「Great Wall」. SDSS 巡天项目中发现了一条长达亿光年尺度的结构,请大家用自己喜欢的方法 (KDE、k - NN 等) 画出它的二维分布.
更新日志
2025/11/13 14:25
查看所有更新日志
de44d-feat(note): add pf note于
