提示

Quizzes

1. 给定信息 $I$，数据 $D$，模型 $M$ 和参数 $\theta$，那么

   1. 先验 (prior)：$P(\theta|MI)$

   2. 似然 (likelihood)：$P(D|\theta MI)$

   3. 后验 (posterior)：$P(\theta|DMI)$

   4. 证据 (evidence)：$P(D|MI)$

      可以用 marginalization 来计算.

   5. Bayes 定理：

      $$P(\theta|DMI)=\frac{P(\theta|MI)P(D|\theta MI)}{P(D|MI)}$$

2. 什么是 Monte-Carlo？

   均匀地随机采点，然后采完之后做平均.

3. 什么是 Important Sampling？

   因为有些点的 likelihood 很低，所以可以没有必要过多地采样这些点，相当于在 Monte-Carlo 上面加一个分布函数去采样，我们希望这个分布函数和我们的后验尽可能一样.

4. 如果我们在做 MC 采样时，增加了 100 倍数据量，那么误差应该？

   有一个常见的关系，$\sim N^{-1/2}$.

5. 对于 MCMC 算法，下面哪一个正确？

   1. 每个点取决于上一个点.
   2. ……

   一个陷阱是，MCMC 不能直接得到证据，同时，MCMC 并不会最终收敛到一个点.

6. MCMC 的 issues？

   1. Incomplete burn-in

      Burn-in 时间太短会造成 bias.

   2. High auto-correlation

      点与点之间关联太强，那么就会造成大量的浪费.

   3. Too wide & too narrow

      可能会跑得太远造成浪费，也有可能被 trap.

7. HMC？

   ……

8. nested sampling (V.S MCMC)

   1. 更准确
   2. 内置的模型选择
   3. 副产品是 evidence
   4. 可以不需要调参数
   5. 对于多峰的分布更加 robust
   6. 需要 gradient information

   选择 b, c, e.

   不选择 a，是因为准确度取决于不同的实际问题.

这节课要开始讲应用了.

Nonparametric Statistics (非参数统计)：我们探索未知的理论时，并不知道特别好的函数形式，所以现在需要一个 flexible 的模型来描述可能的函数形式；同时，要充分利用好先验的作用，因为这时我们的知识非常少；另外，为了表达我们的未知模型 (足够 flexible)，需要大量的参数，这和 Occam's Razor 是违背的，因此还需要一个方式来描述我们的复杂程度.

Model Forms and Representations

「Fit what you know, soften what you do not know.」

已经有 $D$ 和 $I$，确定最后的 $f(x)$.

第一种情况是我们已经非常了解 $f(x)$，这就是一个测电阻的实验，我们的操作是把估计函数变成了估计确定形式的函数的一个参数；第二种情况是我们大概知道是哪一些函数，那么我们就可以按照上节课的方法，每个模型都试一次，最后计算后验比；第三种情况是最困难的，完全不知道任何函数形式，这一点我们后面会讲到.

现在我们假设某一次测量得到的光谱上有一系列非常 sharp 的发射线，

$$\phi(\lambda)=\sum_{j=1}^M\alpha_j\delta(\lambda-\lambda_j)\quad[\text{photon}\cdot\text{s}^{-1}]$$

考虑像素的影响 ($i$) 和 Gauss 型的一个点扩散函数 (point-spread function, PSF)，宽度为 $w$，现在的谱线变成了一个不光滑的形式.

$$\mu = A\exp\left[-\frac{(x-\lambda)^2}{2w^2}\right]+B$$

总的似然为

$$P(D|fI)=\prod_i\frac{\mu_i^{n_i}e^{-\mu_i}}{n_i!}$$

这节课我们已经不能再忽略分母了.

Case 1

我们知道一定只有三条谱线，

$$\mathcal{L}(\theta)=\sum_i(n_i\ln \mu_i-\mu_i-\ln n_i!)$$

这里也显式写出了分母. 同时因为我们对这些数据的了解程度比较多、数据量比较大，取什么先验并不重要，所以最简单地，直接取 $\pi(\theta)=\text{const.}$.

from scipy.special import gammaln, xlogy

def prior_transform(cube, ranges):
  """Transform unit cube to physical parameters for UltraNest"""
  params = np.empty_like(cube)
  for i, (pmin, pmax) in enumerate(ranges):
    params[i] = pmin + (pmax - pmin) * cube[i]
  return params

def log_likelihood(params):
  """Log-likelihood function for spectrum data (x,spec)"""
  if params[1] < params[0] or params[2] < params[1]:
    return -1e99 * params[:3].sum()   # enforce lam1 <= lam2 <= lam3
  mu = spec_model(x, lam=params[:3], A=params[3:], B=50, w=2)
  loglike = xlogy(spec, mu) - mu - gammaln(spec + 1)
  return loglike.sum()

这段代码的目的是，去掉三个谱线的对称性，也就是要求三个谱线存在 $\lambda_1<\lambda_2<\lambda_3$ 的关系，如果不满足这样的关系，就返回一个 -1e99 的极小似然，建立一堵「墙」；同时还要给一个小的常数，产生一个「斜坡」，让 Markov chain 知道怎么跑回来.

另外介绍一个 code trick，在很久以前跑过的 nest 算法之后，想要重新读出来要使用 read_file 函数，这个函数没有很好的文档，所以必须要提一下：

from ultranest.integrator import read_file
from getdist import plots, MCSamples

# Load UltraNest results (same as that returned by sampler.run())
_, results = read_file(log_dir, x_dim=len(param_names))
ws = results['weighted_samples']

# Create (weighted) getdist MCSamples object with hard prior ranges
mcsample = MCSamples(samples=ws['points'], weights=ws['weights'],
    loglikes=-ws['logl'], names=param_names, labels=param_labels,
    ranges={n:p for n,p in zip(param_names, param_ranges)},
    sampler='nested')

# Make the posterior triangle plot
g = plots.get_single_plotter()
g.triangle_plot(mcsample, filled=True)

如果不用 slides 上面的代码，最后得到的图片一定会有问题. 按照上面那些代码可以得到这样的图片：(蓝色是最终拟合，直方图是数据，其他是 MAP 给出的谱线位置，蓝色线的阴影是我们得到的每个点的标准差)

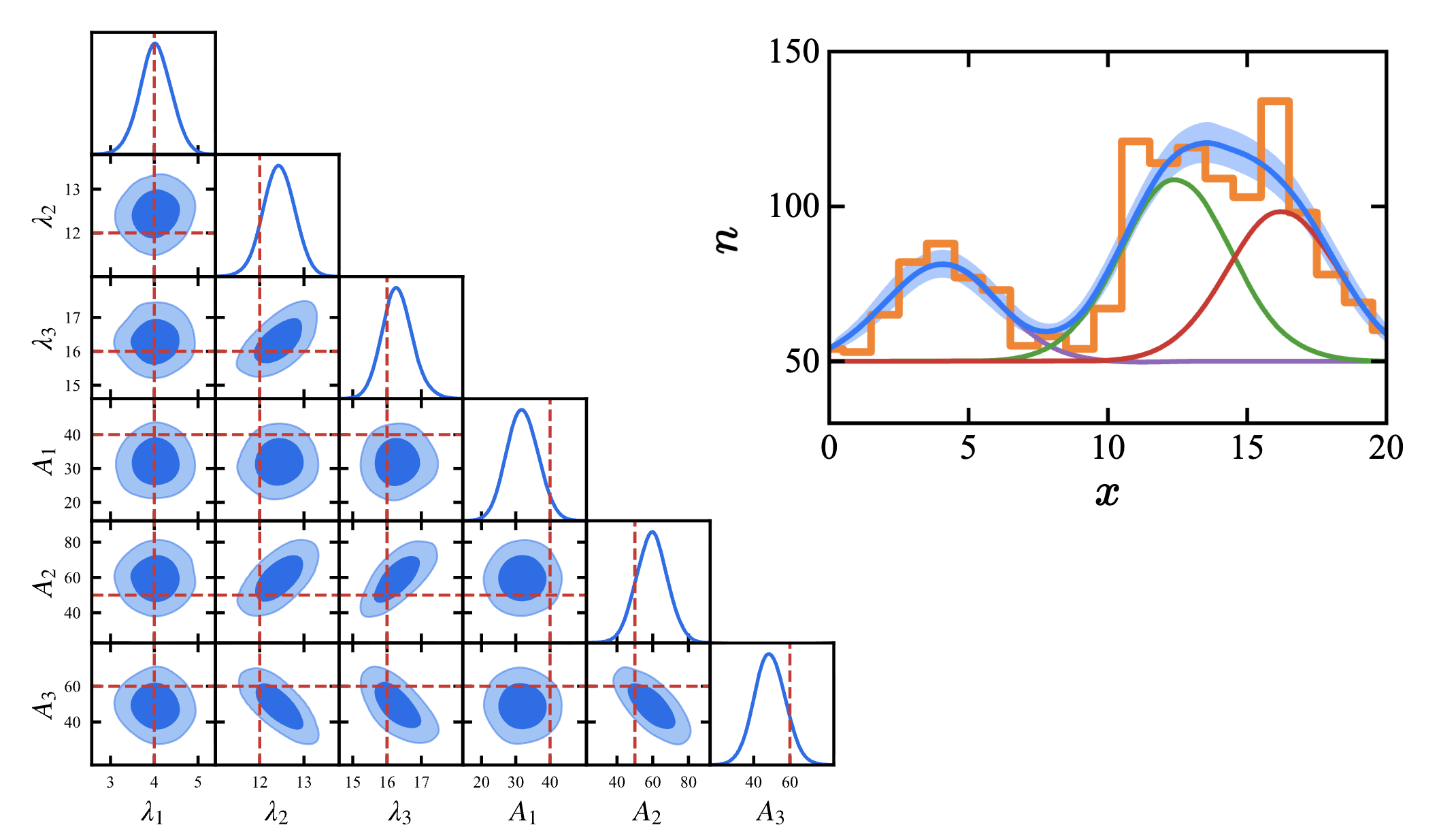
Case 2

现在我们要做模型选择，

$$\mu_{2,i}^{(M)}=\mu_2(x_2;M)=\sum_{j=1}^M\left\{ A_j\exp\left[-\frac{(x_2-\lambda_j)^2}{2w_j^2}\right]+B_j\right\}$$

我们现在甚至不知道到底有几条谱线.

所以尝试跑 2 条谱线的模型、4 条谱线的模型，最终得到下面的结果：

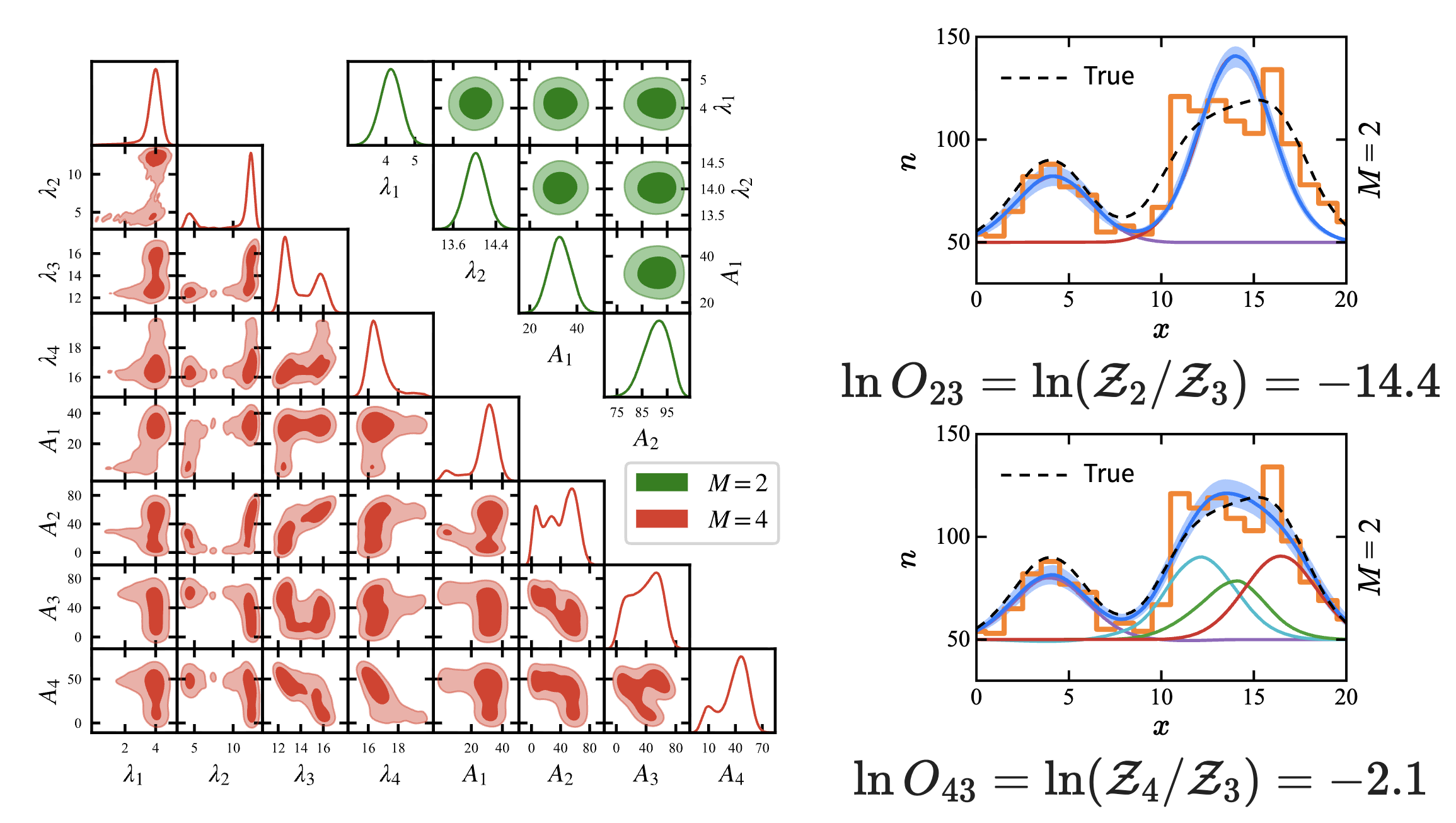
后验比：$\ln O_{23} = \ln(\mathcal{Z}_2/\mathcal{Z}_3)=-14.4$，$\ln O_{43}=\ln(\mathcal{Z}_4/\mathcal{Z}_3)=-2.1$. 根据经验，后验比绝对值超过 $5$ 就可以给出决定性结果，这里可以排除掉 2 条谱线的模型；4 条谱线的模型被 Occam's Razor 所抛弃，最后的结果还是和 case 1 一致.

Case 3

现在我们什么都不知道了. 为了减少所用的参数到可数的范围，我们只能取一些弱假设 (不改变问题的性质的那些假设).

没有参数化的模型，所以一个最简单的想法是，给每一个像素点都找一个值. 但是这样会产生巨量的参数.

更加折衷的方案是，考虑基函数展开：

$$f(x)=\sum_{l=1}^\infty b_lh_l(x)$$

对于这个问题，我们知道谱线是点扩散函数，所以拿 Gauss 分布作为基函数展开；在数据中的 21 个区间内，取 11 个中心值，用 11 个参数进行拟合，结果如图：

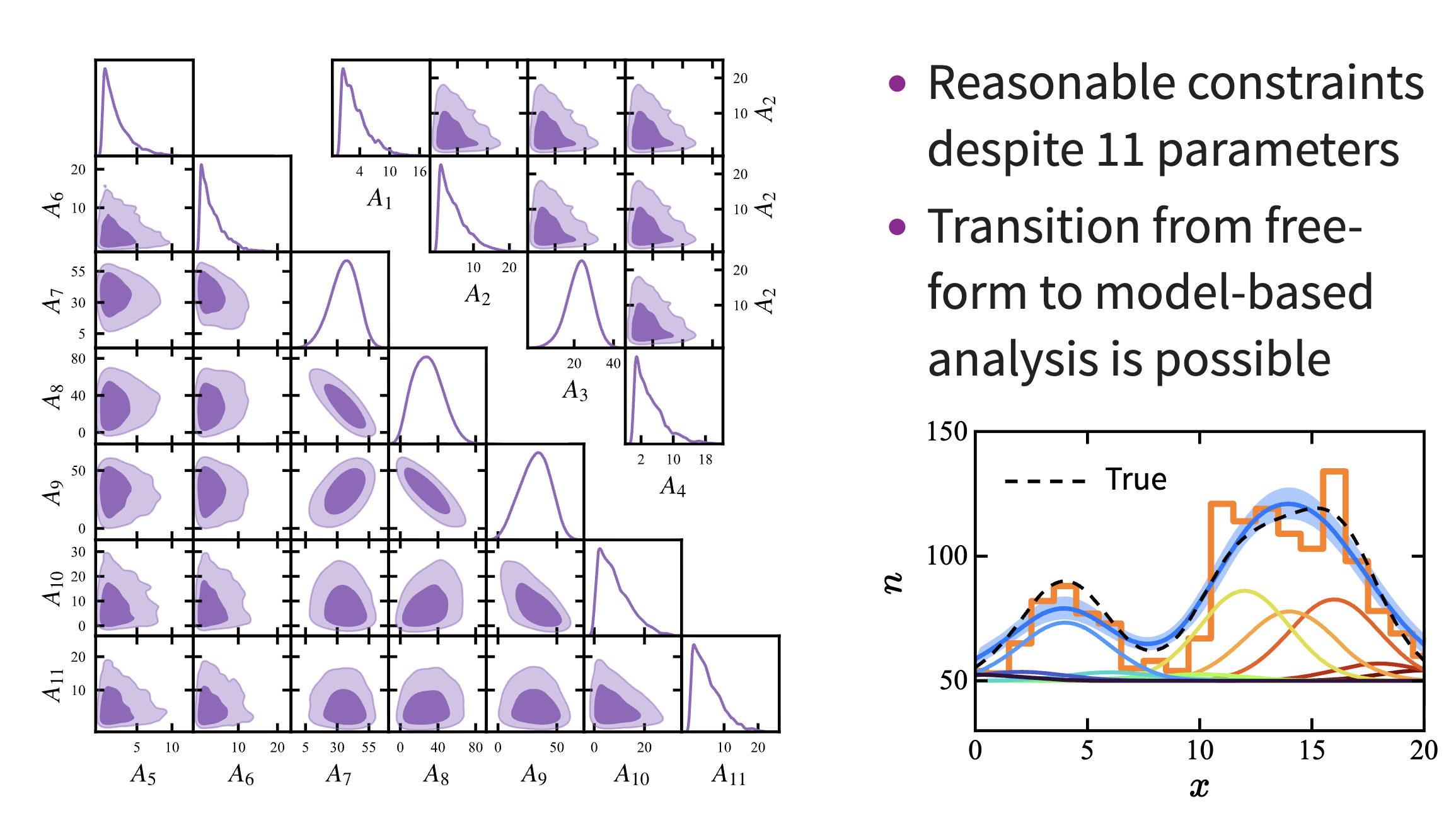
可以看到图中占据主导作用的只有 2 - 4 个峰，这说明我们已经找到了一个不错的函数形式，下一步该缩减参数了，于是我们下一步合理的操作就是缩减这 11 个参数，用 2 - 4 个参数来拟合，接近正确答案.

Gaussian Process Regression

除了直接做参数的先验，我们应该还有其他方法. 下面进入早期机器学习的领域.

我们现在不做参数的先验，而是做函数的先验：$P(f|I)\sim\mathcal{N}(\vec{m},\bold{K})$

• 输入的参数 $\vec{X}=\{x_1,\cdots,x_n\}$ 被 Gauss 分布所产生：

  $$f(\vec{X})\sim\mathcal{N}(\vec{m}(\vec{X}),\bold{K}(\vec{X},\vec{X}))$$

• Gauss 分布是常见的，所以这个方法并不仅仅适用于 Gauss 型的分布.

核函数 (kernel function)：$k(x_i,x_j;\theta)$，with hyperparameters $\theta$.

常取的一个核函数是 Radial basis function (RBF)，类似 Gauss 分布

$$k(x_i,x_j)=\sigma^2\exp\left[-\frac{(x_i-x_j)^2}{2l^2}\right]$$

还有周期性的

$$k(x_i,x_j)=\sigma^2\exp\left[-\frac{2\sin^2(\pi|x_i-x_j|/p)}{l^2}\right]$$

或者线性的. 这些核函数描述的是每两个坐标上的函数值关联大小，直观来看，一个点和自身的关联是 $1$，越往远处走，关联性就会出现变化，可能是越来越小，也可能存在周期性. 用一个核函数 (2 个参数 $\sigma,l$)，可以确定一族函数.

用一组训练集 $(X,Y)=(x_i,y_i)_{i=0}^n$ 来优化超参数：

$$P(\theta|X,Y)\propto P(Y|X,\theta)P(\theta)$$

证据：

$$P(Y|X,\theta)=\int P(Y|f,X,\theta)P(f|X,\theta)\text{d}f$$

这是在函数空间里面的一个积分.

从训练集中，我们学会：

$$\begin{bmatrix} Y\\f(X^*) \end{bmatrix}\sim\mathcal{N}\left(0,\begin{bmatrix} \bold{K}(X,X)&\bold{K}(X,X^*)\\ \bold{K}(X^*,X)&\bold{K}(X^*,X^*) \end{bmatrix}\right)$$

即得到一个联合分布.

最后得到一个「函数的概率云」，函数可以在范围内自由变动；但是一旦给定一个点的函数值，在这一点的函数就会「坍缩」.

下面的代码是我们课程第一次使用机器学习的工具包：

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

lambdas = [4, 12, 16]
As = [40, 50, 60]
x, spec = sim_spec(lambdas, As, B=50, w=2)
spec_var = spec             # Poisson variance

kernel = 1 * RBF(length_scale=1, length_scale_bounds=(0.1,10))
GP = GaussianProcessRegressor(kernel=kernel, alpha=spec_var,
    n_restarts_optimizer=9)
GP.fit(x.reshape(-1,1), spec.reshape(-1,1))

# Generate the credible intervals
x_sp = np.linspace(0, 20, 1000).reshape(-1,1)
mean, std = GP.predict(x_sp, return_std=True)

得到的结果：

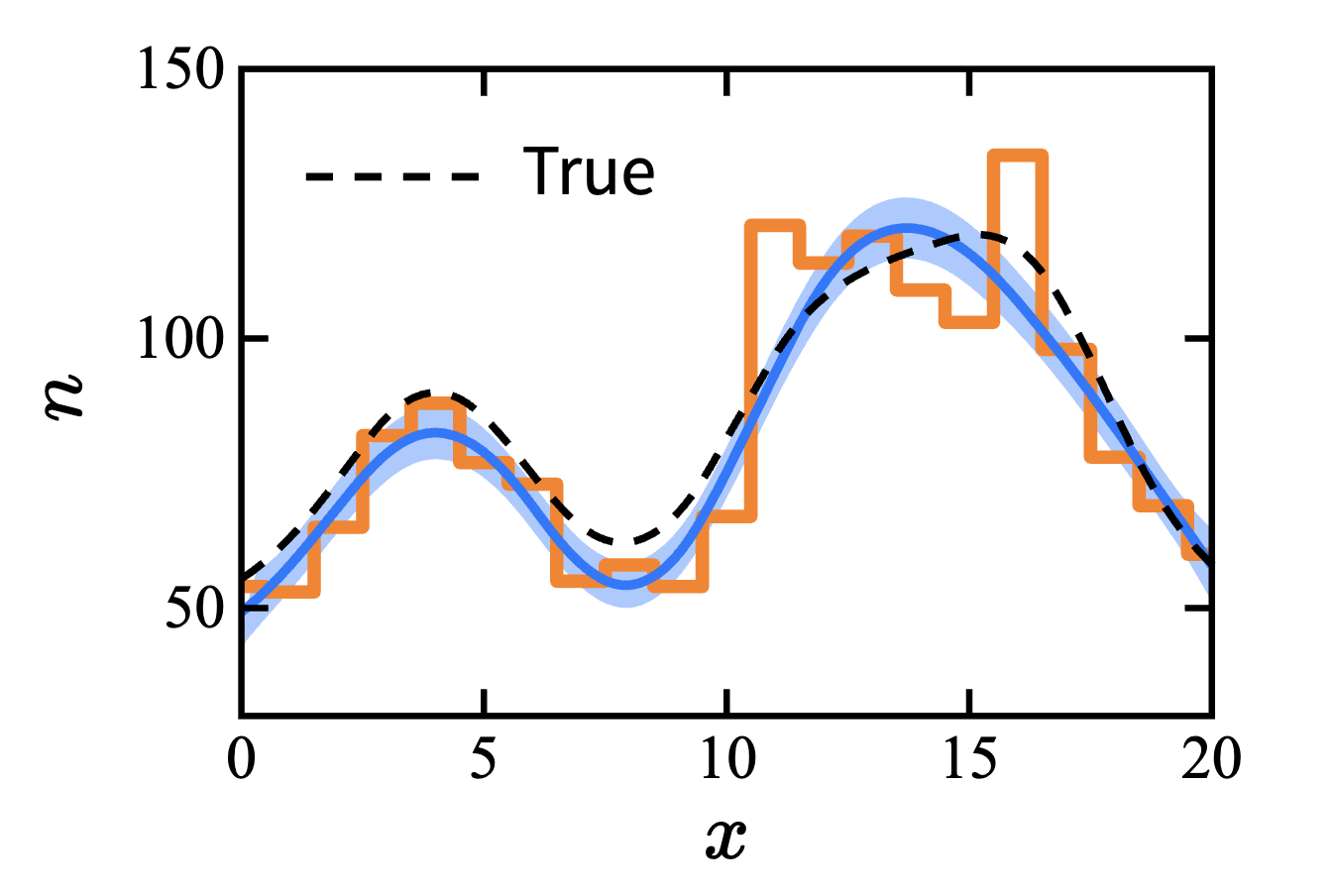
我们的假设只有：函数是平滑的，而且在一定范围里面，基函数是 Gauss 的. 这已经能够得到足够好的结果 —— 函数在每一点的值可以被较为准确地写出. 当然如果想要得到「有几条谱线」的答案，已经可以化为 Case 2 来做.

Maximum Entropy Principle

回到我们课程最开始的问题：统计如何表达我们的无知？也就是，Gauss 分布究竟在什么程度上表达了我们是无知的？为什么我们一开始要采用 Gauss 分布？

一个好的分布函数的前提是：

• 连续性
• 单调性，更大的概率表征更不确定
• 不变性，不同问题得出相同结果

满足这些条件的最佳函数是

$$H_i=\sum_i-p_i\ln p_i$$

这正是熵，Shannon 的信息熵.

我们知道在最无知的情况下，$\{p_i\} = \{1/n\}$. 更深层次的原因是，要求信息熵的最大值，做 Lagrange 乘子法得到的就是等概率原理. 因此我们可以说，最大熵原理是更基本的一条原理. 如果进一步地，我已经知道了

$$\int xp(x)\text{d}x=\mu,\quad \int(x-\mu)^2p(x)\text{d}x=\sigma^2$$

也就是在变分时再加入两个 Lagrange 乘子. 最后我们得到了 Gauss 分布：

$$p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]$$

Exercise

• Given the simulated light curve, predict the brightnesses of the star at along with the uncertainties
• Try Gaussian process regression [online example] with an appropriate kernel
• If time permits, try also predictions via parameter inference (assume the model is known)

更新日志

2025/11/6 16:14

查看所有更新日志

• 1d3c9-feat(note): add as & ed note于 2025/11/6

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)

贡献者: physnya

上一页Lesson 7 Regression & Samplers

下一页Lesson 9 Density Estimation