提示

Quizzes

1. 给定信息 $I$、数据 $D$ 和假说 $H$，则

   1. Prior (先验)：$P(H|I)$

   2. Likelihood (似然)：$P(D|HI)$

   3. Posterior (后验)：$P(H|DI)$

   4. Evidence (证据)：$P(D|I)$

   5. Bayes 公式：

      $$P(H|DI)=\frac{P(D|HI)P(H|I)}{P(D|I)}$$

2. 我们用什么量来判断假说成立的可能性大小？

   后验比 (Posterior (log -) odds)

3. 做二元的假设检验 ($H$ vs $\bar{H}$)，写出后验比：

   $$O_H=\frac{P(H|DI)}{P(\bar{H}|DI)} = \frac{P(D|HI)P(H|I)}{P(D|\bar{H}I)P(\bar{H}|I)}$$

4. 怎么通过后验比的值来判断假说的可信度？

   $O_H\gg1$，prefer $H$；$O_H\ll1$，prefer $\bar{H}$；如果 $O_H\sim1$，那么我们无法区分这两种假说.

5. 我们得到了可信的、但是很不合理的数据，和我们已有的所有假说都不符合，那么我们下一步最好怎么做？

   考虑引入一个新的假设，这个假设的先验很低但是能够解释我们的现象.

   这是科研最难的部分之一 —— 提出新的模型和假说.

6. 什么时候一个「死假设」会「复活」？

   当数据比较极端但是支持死假设时.

7. 重复进行很多次实验，那么某一个特定假设的正确可能性会随着实验次数单调变化

   不止一个假说时，不一定单调.

8. 冗余参数是什么？

   一个连续化的参数 $f$ (比如正面硬币概率)，我们并不觉得它很重要，只需要它在一个区间中，所以可以积分掉这个参数 (也就是边缘化，marginalization)

9. 数据一定会让观点趋同吗？

   错. 同样的数据可以支持相反的观点.

10. 给定模型 $M$ 和模型的参数 $\theta$，则 Bayes 公式中的 $M$ 和 $I$ 可以视为一体的：

    $$P(\theta|DMI)=\frac{P(D|\theta MI)P(\theta|MI)}{P(D|MI)}$$

11. 证据是什么？

    $$E(M)=P(D|MI)=\int P(D|\theta MI)P(\theta|MI)\text{d}\theta$$

12. Bayes 因子是什么？

    $$Q_{ij}=\frac{E(M_i)}{E(M_j)}$$

    这个会乘在我们之前的后验比上面.

13. 什么是 Occam's razor？

    在两个模型拟合数据的效果差不多时，我们倾向于选择参数更少、参数跑动空间更小、更简单的理论.

相关性 $\neq$ 因果性.

Multi-parameter Posterior

前面 $1/3$ 学期一直在抛硬币，现在我们终于来研究天文问题了. 我们来研究光谱，用 Gauss 分布来描述一个连续的谱：

$$\phi(\lambda) = \alpha\exp\left[-\frac{(\lambda-\lambda_0)^2}{2w^2}\right]+\beta$$

模拟：

import numpy as np

def expected_counts(x, A=50, w=5, B=50, lam0=0):
  """Compute expected photon counts at channels x
  Note that A and w may be ndarrays for posterior sampling"""
  n = [A * np.exp(-(xi - lam0)**2 / (2 * w**2)) + B for xi in x]
  return np.array(n)

def sim_spec(A=50, w=5, B=50, lam0=0, m=1, M=51, seed=42):
  """Simulate a spectrum with given parameters"""
  x = (np.arange(M) - M // 2) * m         # channel centers
  nexp = expected_counts(x, A=A, w=w, B=B, lam0=lam0)
  rng = np.random.default_rng(seed)
  num = rng.poisson(nexp)                 # simulated counts
  return x, num

($\beta$ 是一个噪声) 光子量为 $mt\phi(\lambda)$. 我们期望，将这个探测到的连续数据离散化，得到分立的谱线.

之前我们说过，光子的分布符合 Poisson 分布：

$$P(n_i\equiv n(x_i)|N_i)=\frac{N_i^{n_i}e^{-N_i}}{n_i!}$$

如果 $\alpha mt=\beta mt=50$，信噪比是多少？

信号 $S=50$，这是显然的；噪声和信号都符合 Poisson 分布，它们的叠加意味着平均值相加，而噪声是 $\sqrt{\mu}$ (平均值的平方根)，所以噪声 $N=\sqrt{50+50}=10$，信噪比是 $5$，这在天文上已经很难得了.

考虑 $\lambda_0$ 和 $B=mt\beta$ 已经给出了，未知量只有 $A$ 和 $w$. 由 Bayes 定理，得到

$$p(A,w|n_i,I)\propto p(n_i|A,w,I)p(A,w|I)$$

假设每次的数据都是独立的，

$$p(\{n_i\}^M_{i=1}|A,w,I)=\prod_{i=1}^Mp(n_i|A,w,I)=\prod_{i=1}^M\frac{N_i^{n_i}e^{-N_i}}{n_i!}$$

这里的乘积太大了，考虑取对数，得到

$$\begin{aligned} \ln p(A,w|\{n_i\},I)&=\ln p(\{n_i\}|A,w,I)+\ln p(A,w|I)\\\\ &=\sum_{i=1}^M(n_i\ln N_i-N_i)-\ln(Aw)+\text{const.} \end{aligned}$$

取 $\ln$ 之后，因为数据已经给定，所以 $n_i$ 的那些项实际上是常数，我们的计算被简化了很多.

最终我们将得到一个 $A$ - $w$ 平面上的等高线图 (等 $\sigma$ 线图)：对于二维分布，$1\sigma$ 对应 $39.34\%$、$2\sigma$ 对应 $86.47\%$、$3\sigma$ 对应 $98.89\%$.

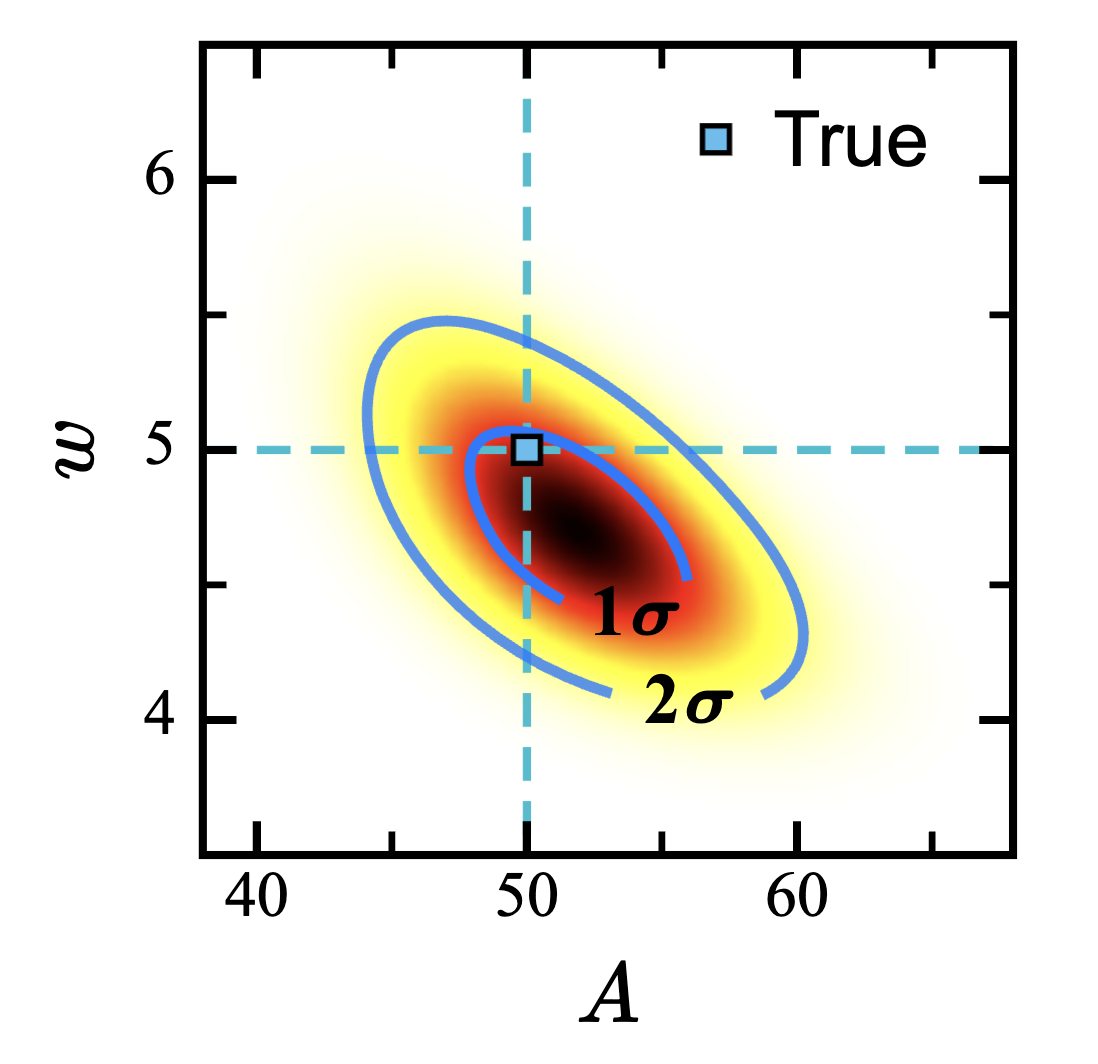
但是我们觉得给出一个图片并不是足够说明问题，所以我们需要投影到两个轴上面，这又是我们提到过的边缘化 (marginalization)：这里的冗余参数是我们不关心的那一个，需要将它积分掉. 投影之后按照一维的方式来估测我们的真值、误差等等.

我们的工作做完了吗？

并没有！

我们没办法从两个一维的分布把之前的二维分布重建出来了，所谓的重建只能得到一个很「正」的椭圆.

Correlation & Degeneracy

(关联和重建)

高维的方差定义为：

$$C(\theta)=\braket{(\theta-\braket{\theta})(\theta-\braket{\theta})^T}=\begin{pmatrix} \sigma_1^2&\rho_{12}\sigma_1\sigma_2&\cdots&\rho_{1n}\sigma_1\sigma_n\\ \vdots&\ddots&\ddots&\vdots\\ \sigma_n\sigma_1&\rho_{n2}\sigma_n\sigma_2&\cdots&\rho_{nn}\sigma_n^2 \end{pmatrix}$$

这里的非对角元定义为协方差，矩阵称为协方差矩阵. 在这个问题中，我们的协方差是

$$\braket{(A-\braket{A})(w-\braket{w})}$$

当然，协方差矩阵的计算只需要一行 numpy 的代码罢了. 用协方差矩阵重建这个二维分布时，我们发现每个单维度的分布并无变化 (只由对角元决定)，而重建出来的二维分布不再是之前的一个椭圆，而是很接近我们最开始测量到的数据.

当我们重建出这个二维分布时，我们发现，$A$ 增大时 $w$ 减小，只有这样的模型才能够满足我们的这个关系. 回到物理的情景，实际上意味着当光谱的峰值提升，光谱的宽度应该降低，这是由光子数守恒 (面积守恒) 所决定的.

通过观察协方差矩阵来判断数据的关联模式：对角元决定了长轴 / 短轴的宽度 (椭圆的胖瘦)，非对角元的正负性决定了相关关系是正相关还是负相关，非对角元越大、相关性越强.

如果把协方差矩阵 (Covariance Matrix) 归一化，得到 Correlation Matrix：

$$\bold{R}=\begin{pmatrix} 1&\rho_{12}&\cdots&\rho_{1n}\\ \rho_{21}&1&\cdots&\rho_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ \rho_{n1}&\rho_{2n}&\cdots&1 \end{pmatrix}$$

这个矩阵的矩阵元 $\in[-1,1]$.

假设两个参数 $\theta_i$ 和 $\theta_j$ 不相关，则它们的 $\rho_{ij}=0$，协方差：

$$\braket{(\theta_i-\braket{\theta_i})(\theta_j-\braket{\theta_j})}=\braket{\theta_i\theta_j}-\braket{\theta_i}\braket{\theta_j}=0$$

这和我们之前说到的独立事件的式子很像.

那么我们看看下面的论断：

1. 独立事件一定不相关
2. 不相关事件一定独立
3. 完美独立的事件的相关系数一定是 $\pm1$
4. 如果两个变量都和第三个变量强相关，那么它们之间一定相关

首先对于 3.，我们课程只考虑线性的相关性，所以是对的；对于 4.，我们能够构造出一个非常扁的圆柱，它在某个平面上投影是一个圆 (完全不相关)，而在另外两个平面上投影都是直线 (完全相关). 所以实际上只有第一个论断是正确的，因为「独立」是一个极强的条件.

在上面的问题中，我们还能够对单个变量进行估计：先猜测一个 $A$ 值然后估计 $w$. 我们发现，猜错 $A$ 会导致 $w$ 出现比较大的偏差.

如果我们强行固定 $A$ (自由参数)，会得到更小的不确定度，也会出现更大的 bias —— 这是不好的，因为我们的数据应该忠实地反应我们对现实的了解程度，不能有意地加强先验来获得更小的不确定度，何况这样可能产生更大的偏差.

Derived Parameters

假设我们的 $w$ 来源于恒星的 Doppler 效应，恒星的速度展开正比于 $w$：

$$\sigma_v=10w$$

最无脑的思路是，把 $w$ 换成 $\sigma_v$，在之前的计算中完全用 $\sigma_v$ 来操作. 但是这样有点太麻烦，我们可以用上面的关系来直接确定两种分布之间的关系，在这里是形状相同的两个分布.

但是如果是 $f=Aw/10$ 的分布呢？

用 Jacobian：

$$|\nabla g|=\begin{vmatrix} w/10&A/10\\0&10 \end{vmatrix}=w$$

则 114514

$$p(f,\sigma_v|D,I)=p(A,w|D,I)\cdot$$

考虑 $\vec{y}$ 是由 $A$ 和 $w$ 两个分量构成的矢量，换成另外两个，那么得到了所谓误差传递公式：

$$\sigma_z=\begin{bmatrix} \frac{\partial y}{\partial A}\\\frac{\partial y}{\partial w} \end{bmatrix}^{-1}\begin{bmatrix} \sigma_A^2&\sigma_A\sigma_w\\ \sigma_w\sigma_A&\sigma_w^2 \end{bmatrix}\begin{bmatrix} \frac{\partial y}{\partial A}\\\frac{\partial y}{\partial w} \end{bmatrix}$$

当然我们高中竞赛的时候不会考虑这些交叉项.

Exercise

固定 $A$，做 $B$ 和 $w$ 的统计.

独立的数据产生的结果可以叠加：

$$p(f,\sigma_v|D_1D_2I)=p(f,\sigma_v|D_1I)\cdot p(f,\sigma_v|D_2I)$$

原则上这样的叠加会让二维图上整个区域变小，但是可能会出现下面的情况：

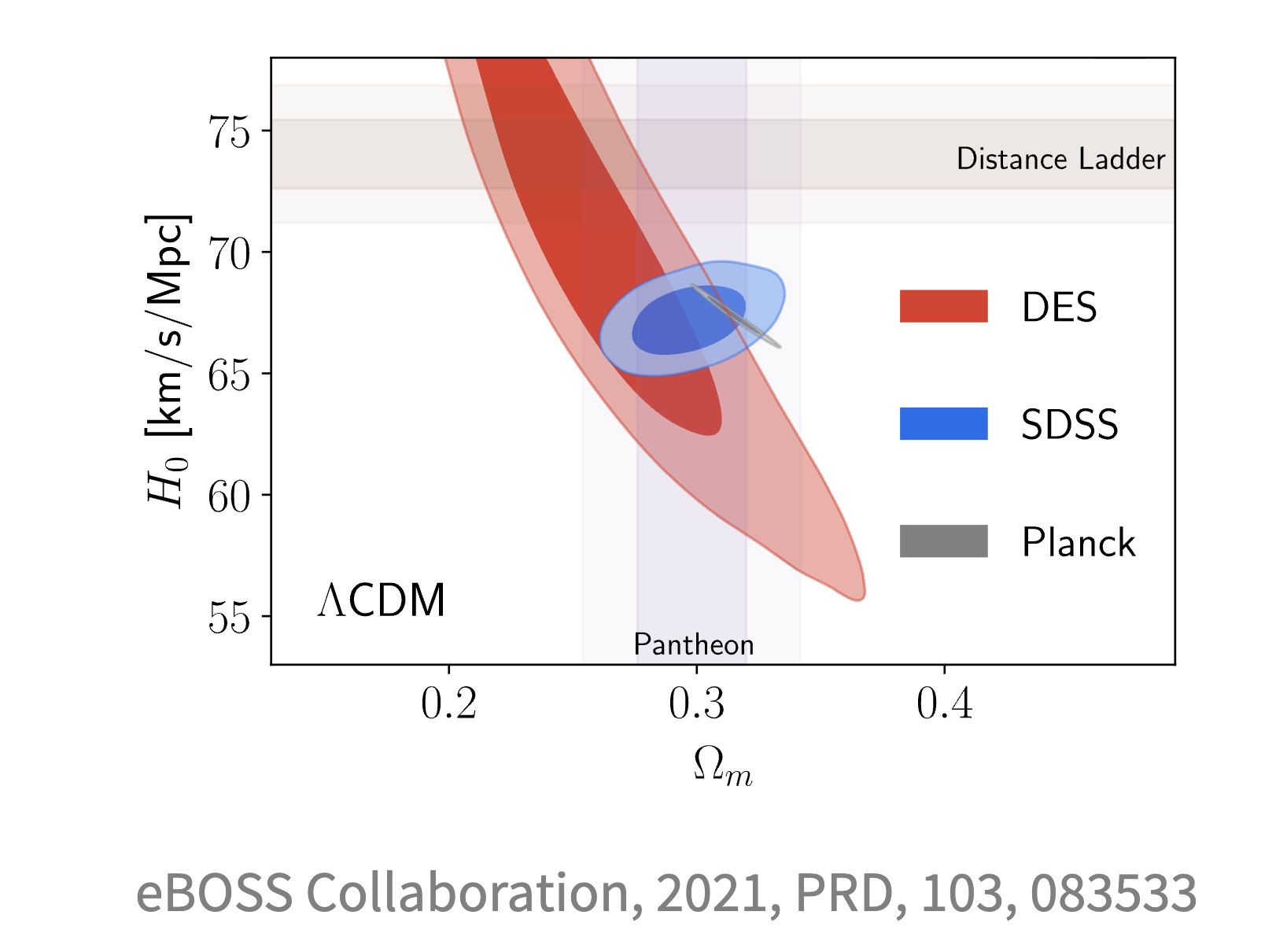
这来源于对理论的解读不同，也可能是系统误差.

更新日志

2025/10/23 14:10

查看所有更新日志

• 282d7-feat(note): add as note于 2025/10/23

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)