提示

Quizzes

1. 概率论的乘法规则是什么？

   $$P(AB|I)=P(A|BI)P(B|I)=P(B|AI)P(A|I)$$

   (我们再次再次回顾这个规则)

2. 概率论的加法规则是什么？

   $$P(A|I)+P(\bar{A}|I)=1$$

3. 加法规则的推广？

   $$P(A+B|I)=P(A|I)+P(B|I)-P(AB|I)$$

   如果 $A$ 和 $B$ 互斥，最后一项就没有了.

4. 给出表达式：

   1. Prior (先验)？

      $$P(H|I)$$

   2. Likelihood (似然)？

      $$P(D|HI)$$

   3. Posterior (后验)？

      $$P(H|DI)$$

   4. Evidence (证据)？

      $$P(D|I)$$

   5. Bayes' Theorem？

      $$P(H|DI) = \frac{P(D|HI)P(H|I)}{P(D|I)}$$

5. 在一个合理的先验下，更多的数据对后验造成什么影响？

   1. 后验更接近真相了.
   2. 后验变宽，包含了真值.
   3. 后验的峰值更窄，接近真值.
   4. 取决于先验，无法分辨.

   答案应该选 a. 和 c.，因为后验应该是变窄的、向真值集中，而且数据越多我们了解的程度一定更深；但是如果真值有两个峰值，c. 也有可能是错的.

6. 有哪些估计真值的方式？这几种方法分别如何估计误差？

   我们可以用均值、中位数或者峰值来估计.

   1. 均值估计的误差是用标准差来估计的.
   2. 中位数估计的误差是用百分位数估计的.
   3. 峰值估计的误差可以用「作水平线划定 $68\%$ 的方法」估计.

   但是峰值估计没有其他两个那么好的性质.

7. 什么方法能够最好地呈现一个复杂的后验？

   直接上图！

8. 怎么算一个后验 $p(\theta)$ 的均值和标准差？

   $$\mu=\int\theta p(\theta)\text{d}\theta\,,\quad\sigma=\sqrt{\int(\theta-\mu)^2p(\theta)\text{d}\theta}$$

9. 找到下述表述对应的概念：

   1. 能够最小化误差平方的估计方式：均值估计.
   2. 能够最小化绝对误差的估计方式：中值估计.
   3. 能够最大化后验密度的估计方式：MAP (Maximum a Posteriori)，峰值估计.
   4. 重参数化不影响结果的估计方式：中值估计 (任意百分位数估计).

10. 判断题：

    1. 三种估计在对称且单峰的先验下，得到的真值等价.
    2. 标准差 = 16 / 84 百分位数的对称且单峰的先验，均值估计和中值估计等价. ($\times$)
    3. ...

11. 一个长尾的后验，排序三种估计值.

    $$\text{MAP}<\text{median}<\text{mean}$$

12. 对于独立的数据点 $D=\{d_i\}$，给定模型 $H$ 和背景知识 $I$，似然怎么写？

    $$P(D|HI) = \prod_i P(d_i|H,I)$$

13. 判断：如果样本分布没有有限的均值和标准差，那么统计不可做.

    并非，因为在真值处的概率仍然可观.

这节课我们说模型选择，这是比较难而且「坑」很多的一个部分. 我们在上节课学会了数学公式之后，我们这节课回到自己的常识，用合适的数学工具处理数据并验证是否符合自己的常识.

我们最经常处理的问题是，哪个数学模型 (一次函数、二次函数还是指数函数) 更好地拟合某一串数据点？

假设检验

从 Bayes' Theorem 开始：

$$P(H|DI)=\frac{P(D|HI)P(H|I)}{P(D|I)}$$

如果我们有两种互补的假设，$H$ and $\bar{H}$，Bayes 定理告诉我们，

$$P(H|DI)=\frac{P(D|HI)P(H|I)}{P(D|I)}\,,\quad P(\bar{H}|DI)=\frac{P(D|\bar{H}I)P(\bar{H}|I)}{P(D|I)}$$

如果把这两者做比，应当得到

$$O_{H}\equiv\frac{P(H|I)}{P(\bar{H}|I)}=\frac{P(H|I)}{1-P(H|I)}\,,\quad O_{\bar{H}}=O^{-1}_H$$

这样消掉了归一化常数证据. 如果 $Q_H\ll1$，那么我们选择 $\bar{H}$，反之则选择 $H$；但是如果 $O_H\approx1$ 就无法判断.

推广一些，我们可以对任意的两个假设做后验比，来选择正确的假说. 一般我们使用的是 $\log_{10}O_H$ 或者 $\ln O_H$ 来判断，这是因为人类的判断，或者说感觉，很多时候是对数的.

比如如果人类能够接受月亮的光，那么太阳光的数量比月光大了几个量级，人类的感觉必须要是对数的才能接受这样的差异；

另外，人类对时间的感知也是对数的，18 岁 (年龄对数的中值) 之前对一年的感知是缓慢的，但是到了年纪越来越大，时间会「越来越快」.

提示

真是毛骨悚然的事实啊...

继续玩硬币，假设两个硬币 $A$ 和 $B$：

$$\begin{aligned} f_A &= P(1|AI)=1/2\,,\quad P(0|AI)=1/2\\\\ f_B &= P(1|BI)=1/4\,,\quad P(0|BI)=3/4 \end{aligned}$$

这两个硬币混在一起，我们想要区分它们，就拿出一个硬币做实验. 这里，

• 先验：

  $$P(H|I)=P(\bar{H}|I)=\frac{1}{2}$$

• 似然：

  $$P(D|HI)=\prod_iP(d_i|AI)\,,\quad P(D|\bar{H}I)=\prod_iP(d_i|BI)$$

• 后验比：

  $$O_H=\prod_i\frac{P(d_i|AI)}{P(d_i|BI)}\Longrightarrow\ln Q_H=\sum_i\ln\frac{P(d_i|AI)}{P(d_i|BI)}$$

我们发现，每一次实验都让后验比的对数变化一个常数：

$$\Delta\ln Q_H^{(1)}=\ln\left|\frac{P(1|AI)}{P(1|BI)}\right|=\ln2\,,\quad\Delta\ln Q_H^{(0)}=\ln\left|\frac{P(0|AI)}{P(0|BI)}\right|=\ln2/3$$

所以随着实验数据的增长，$\ln Q_H$ 线性变化，到达某个值时，我们可以开始下判断. 这个概率影响的是 $\ln Q_H$ 的斜率，也就影响我们需要多少次实验才能下判断.

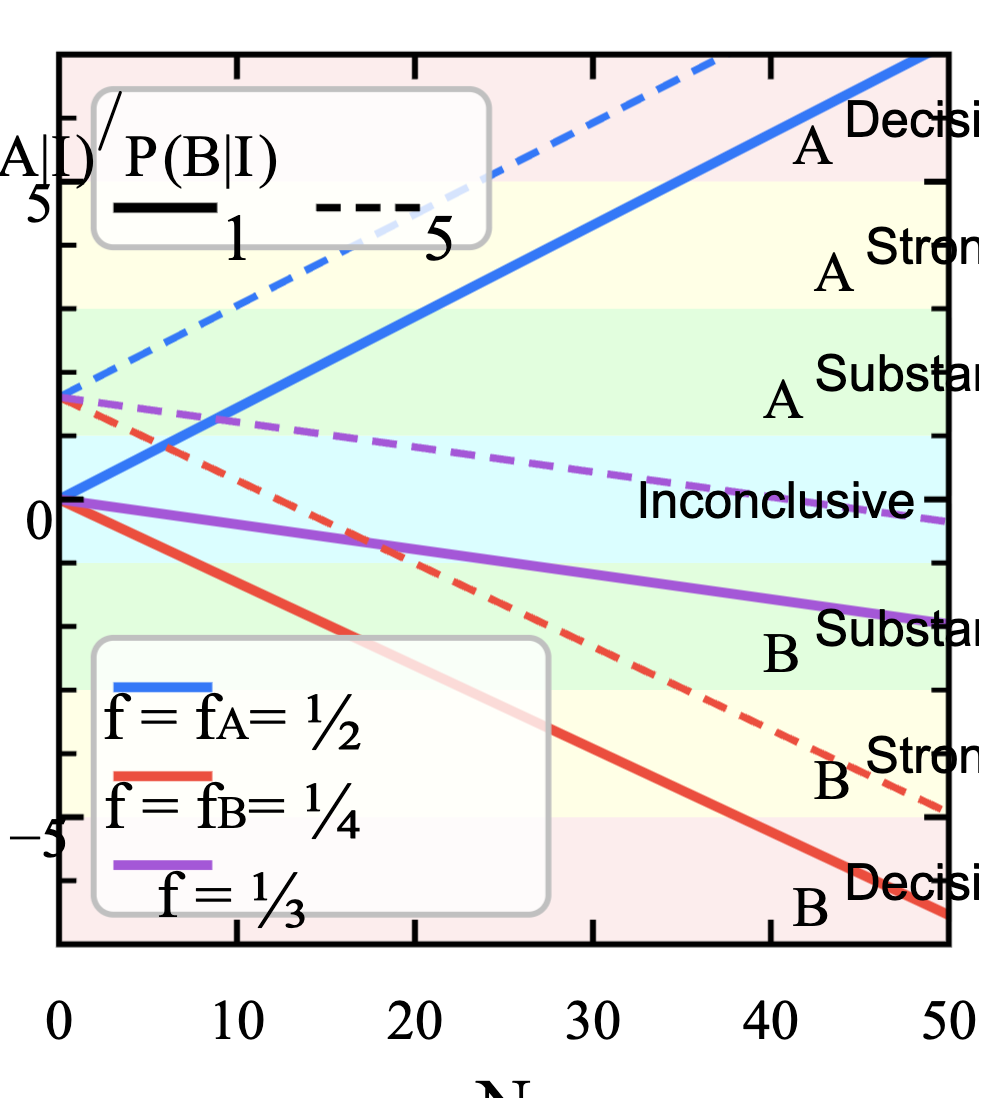
而先验在这里影响的是图像上的截距，比如如果有 5 个好的硬币，1 个坏的硬币，那么我们一开始拿到的就更可能是好的硬币.

---

现在出现了异常的状况：连着 50 次全部是正面.

那么按理来说这里的后验比 $\ln Q_A\approx34.7>5$，非常支持「硬币是好的」这一结论. 但是，如果 50 次全部是正面，你还敢相信这个硬币是好的吗？

所以现在我们要在理论上下一个保险，来保证我们能够对背景知识做出怀疑.

引入一个 $C$ 硬币的「死假设」，它的先验非常小，$P(C|I)=10^{-6}$，而且 $C$ 硬币的抛掷概率是

$$f_C=P(1|CI)=\frac{99}{100}$$

另外两个的先验变小了 $0.5\times10^{-6}$，这是一个几乎可以忽略的影响.

$$O_C=\frac{P(C|DI)}{P(\bar{C}|DI)}=\frac{P(C|DI)}{P(A|DI)+P(B|DI)}=\frac{P(D|CI)P(C|I)}{P(D|AI)P(A|I)+P(D|BI)P(B|I)}$$

50 次都是正面的数据记为 $\hat{D}$，代入，得到的 $\ln O_{A,B,C}$ - $N$ 图像变成了一个类线性的图像：

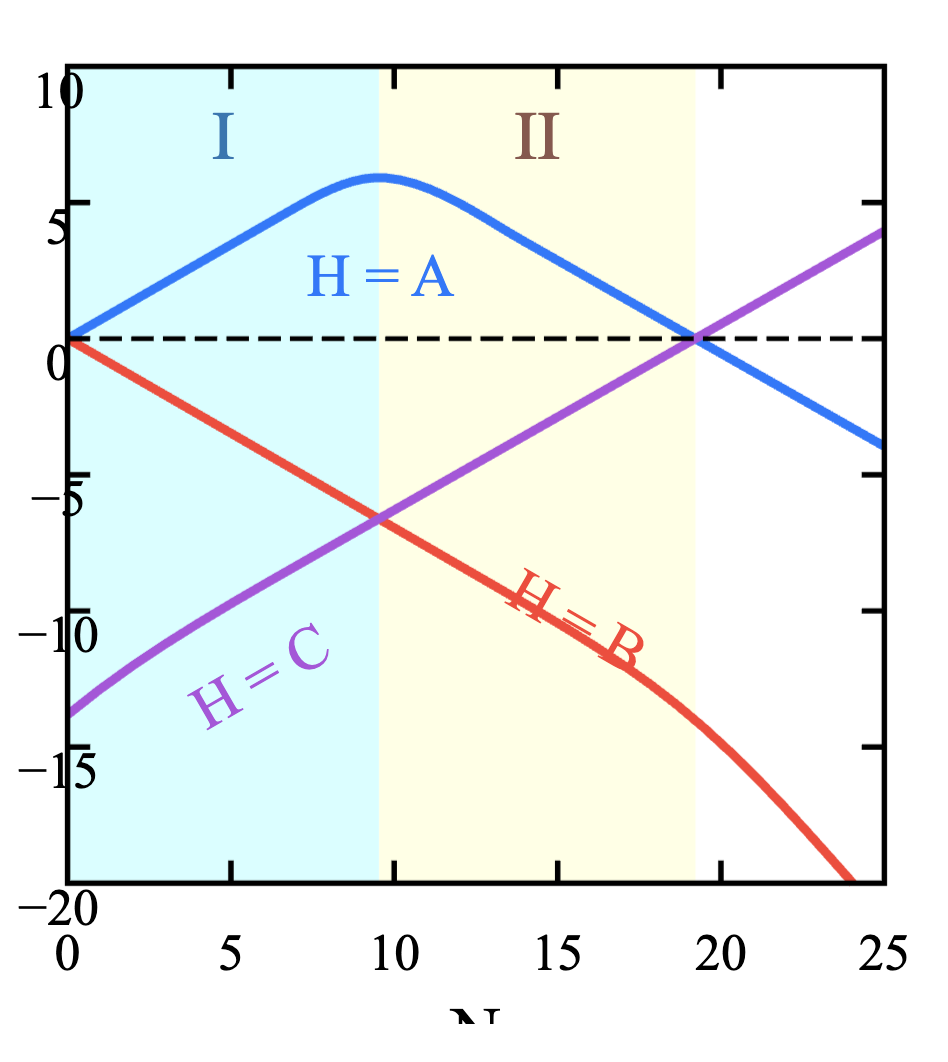
分为三个阶段：

1. $A$ vs. $B$：$C$ 被极小的先验所控制了.
2. $A$ vs. $C$：$C$ 的概率因为实验结果而大幅提升.
3. $C$ vs. $B$：$C$ 占据主导地位.

这里我们也能看到，在极端的实验结果下，一个「死假设」也有可能复活.

备选假说

How do we test if a coin is fair？

除了 $f=1/2$ 以外，其他所有的 $f$ 都不是 fair，这像一个 delta 函数.

我们说，我们的判断应该是 $f$ 在 $1/2$ 邻域的一个小区间 $\Omega$ 就算是 fair. 于是 $\bar{H}=\Omega_c=[0,1]/\Omega$.

所以 $f$ 的值不重要了，我们只关心 $f$ 所在的区间，我们可以把 $f$ 给积分掉，这就是所谓的 marginalization (边缘化)：

$$O_H=\frac{P(D|HI)P(H|I)}{P(D|\bar{H}I)P(\bar{H}|I)}=\frac{\displaystyle{\int_\Omega P(D|f,I)P(f|I)\text{d}f}}{\displaystyle{\int_{\Omega_c} P(D|f,I)P(f|I)\text{d}f}}$$

举一个例子：

在上世纪有一段时间超能力很火，有一位 Stewart 女士声称自己有心灵感应，设计了一个实验：

在一个房间内一个实验员选择一张卡片 (五选一)，这张卡片由另一个实验员确认，进入女士的房间，让她给出答案，到另一个房间换一个人记录.

---

它们一共做了 37100 次实验，其中猜对了 9410 次.

如果每次猜测是独立的，那么这就和抛硬币一样.

我们的先验应该是，超能力不可能出现，所以先验在 $0.2$ 附近应该有一个很窄的峰值：

$$p(f|I)\propto\exp\left[-\frac{(f-0.2)^2}{2\times0.004^2}\right]\,,\quad0\leq f\leq1$$

假说设定，$5\sigma$ 才能认定有超能力，那么

$$H_t=\{f>0.22\}\,,\quad H_0=\{f\leq0.22\}$$

似然是 Bournoulli 分布：

$$p(D|f,I)\propto f^n(1-f)^n$$

后验比：

$$\begin{aligned} O_{t0}&=\frac{P(D|H_tI)}{P(D|H_0I)}\cdot\frac{P(H_t|I)}{P(H_0|I)}\\\\ &=\frac{\displaystyle{\int_{0.22}^{1}P(D|f,I)P(f|I)\text{d}f}}{\displaystyle{\int_0^{0.22}P(D|f,I)P(f|I)\text{d}f}} \approx2.9\times10^{28} \end{aligned}$$

强烈支持有超能力的假说，这还是在先验给得很低的情况下.

---

问题出在哪里？

我们不应该假定 $H_0=\bar{H}_t$，有很多死假设，比如：

• 作弊
• 数据记录错误
• ……

这些死假设满足：$P(H_i|I)>P(H_t|I)$ (这个大于号来源于我们对于超能力的不信任).

那么，这些死假设会像刚刚的 $C$ 硬币一样，后验比直线上升，同时这些死假设的斜率和超能力假设的斜率一样，在实验数量增加时，这些死假设一定会占据主导.

注意

当然你大可以说你对超能力有很深的执念，所以在你看来这个结果应当支持超能力 —— 没有人能反驳你得出的结论.

当然这取决于超能力和作弊的正确率到底是谁更高.

两派的观点在同样的数据下仍然相反. So, what does the data tell？三种观念：

• Let the data speak for themselves. —— R. A. Fisher
• The data cannot speak for themselves; and they never have, in any real problem of inference. —— E. T. Jaynes
• If you torture the data long enough, it will confess to anything. —— Ronald Coase

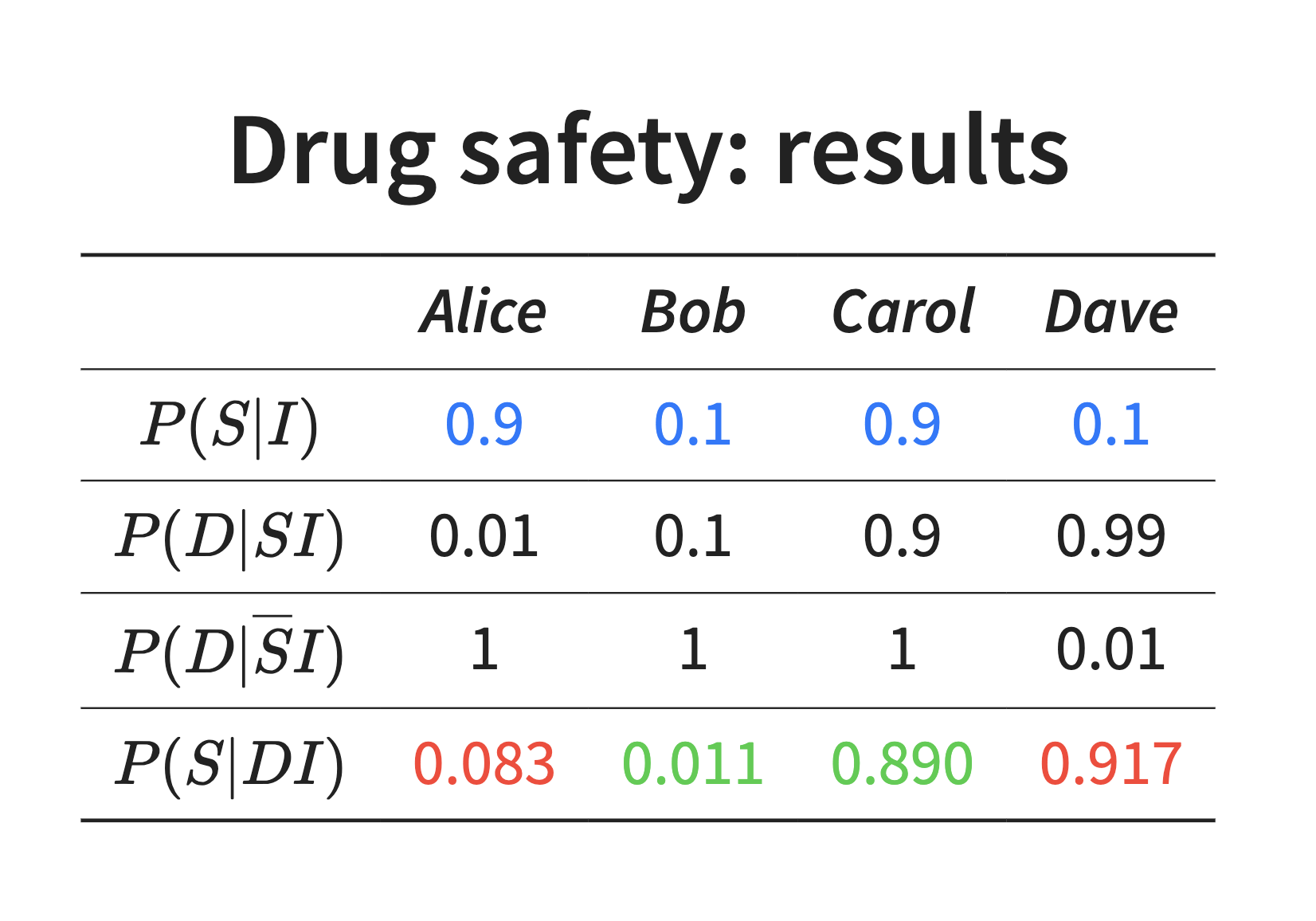
另一个例子是药物不安全的问题

Oscar 公开声明一个普遍使用的药物不安全；

先验：

• Alice 和 Carol 认为药物安全，$P(S|I)=0.9$.
• Bob 和 Dave 认为药物不安全，$P(S|I)=0.1$.

四个人对 Oscar 的观点不同：

• Alice: Oscar is very honest and trustworthy

  $$P(D|SI) = 0.01,\quad P(D|\bar{S}I) = 1$$

• Bob: Oscar is honest, but sometimes makes mistakes

  $$P(D|SI) = 0.1,\quad P(D|\bar{S}I) = 1$$

• Carol: Oscar chases sensational news

  $$P(D|SI) = 0.9,\quad P(D|\bar{S}I) = 1$$

• Dave: Oscar always claims the opposite

  $$P(D|SI) = 0.99,\quad P(D|\bar{S}I) = 0.01$$

四个人

---

算归一化因子：

$$\begin{aligned} P(D|I)&=P(DS|I)+P(D\bar{S}|I)\\\\ &=P(D|SI)P(S|I)+P(D|\bar{S}I)P(\bar{S}|I) \end{aligned}$$

计算得到所有人的观点都会变得更加极端，这正是所谓西方民主的悖论.

天王星的轨道不符合 Newton 定律？

这里还是取决于我们的备选假设是什么.

如果我们觉得广义相对论是对的，那么这个结果就支持广义相对论；如果我们觉得有超自然力量，那么就支持有超自然力量.

现在又发现了海王星，那么这个结论又可以支持「有新的行星存在」.

所以说概率论到这里似乎什么都没有讲：我们从常识得到了概率论，那么我们的结果也就能直接从常识得到，那么概率论并没有意义. 所有的科学发现是因为提出了新的理论，这些理论更加符合我们的世界，这个想法只要有常识就够了.

模型比较

但是真的是这样吗？我们用概率论还能做什么？

我们之前比较的是同一个模型，只有一个参数；但是如果我们比较不同的模型框架呢？

现在，

$$p(\theta|DMI)=\frac{p(D|\theta MI)p(\theta|MI)}{P(D|MI)}$$

证据不再可以被做比的方式消掉，我们必须计算：

$$E(M)=\int p(D|\theta MI)p(\theta|MI)\text{d}\theta$$

那么现在的后验比多了一个新的参数，是证据比：

$$Q_{ij}=\frac{p(M_i|DI)}{p(M_j|DI)}=\frac{E(M_i)p(M_i|I)}{E(M_j)p(M_j|I)}\equiv B_{ij}\frac{p(M_i|I)}{p(M_j|I)}$$

还是用硬币为例，两种模型：

• $M_1$：有一个固定正面概率 $\hat{f}$.
• $M_2$：有一个参数 $f$ 描述正面概率.

用代码模拟，很容易发现，$M_2$ 更加合理.

于是我们说 ($\mathcal{Occam's}\text{ }\mathcal{Razor}$)：更加简单的模型更优秀.

---

为什么会有 Occam's Razor？

回头来看，我们的后验比

$$\frac{E(M_1)P(M_1|I)}{E(M_2)P(M_2|I)}=\frac{E(M_1)}{E(M_2)}$$

因为模型的先验一样，所以后验比取决于证据.

Non sunt multiplication entia sine necessitate. —— John Punch (1639)

更新日志

2025/10/16 14:50

查看所有更新日志

• c2ee2-fix(note): add images于 2025/10/16
• 52926-feat(note): add astro-statistics note于 2025/10/16

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)