外观
Lesson 14 Spatial Statistics
约 2854 字大约 10 分钟
2025-12-18
提示
Quizzes
天文学上有哪些常见的时序数据类型?
周期性;爆发性;啁啾型;随机的信号 (后一时刻信号取决于前一时刻的)
我们在处理时序数据的时候会遇到哪些比较常见的问题?
噪声、采样是不规则的、数据中存在探测极限 / 测量误差...
下面有关 Fourier 分析的表述哪些是对的?
- 将函数分解为三角函数的和
- 短时的信号表达低频信息
- 方便分析周期性数据
- 功率谱展示了每种频率的信号强度
- 如果数据是实数,那么变换也是实数
选 a., c., d..
什么是 convolution theorem?
时域的卷积是频域的乘法,反之亦然.
下面有关离散 Fourier 变换的表述哪些是对的?
用在有限的数据集上
Nyquist 频率是能够探测的最低频率
Nyquist 频率的定义是采样的最高频率
如果在时域采样更密,那么能够减少我们 aliasing 的问题
FFT 是一个有效的获得 DFT 的估算算法
选 a., c..
FFT 是一个严格的算法,不是估算.
下列有关周期图的说法正确的是?
它等价于 Fourier 变换得到的功率谱
周期图可以处理有误差的数据,但是 Fourier 变换实际上并不可以.
周期图上的峰代表了一个很强的频率
选 b..
下列有关时间频率分析的说法正确的是?
- 它们能够展示信号中有哪些频率
- 谱图能够用一个窗口来进行 Fourier 变换
- 小波分析是局域的
- ……
选 a., b., c..
小波功率谱告诉我们什么信息?
在给定时间内,它给出在时间、频率的二维图上的强度.
什么是随机过程?给一个例子.
它在短时间内有小的关联,但是长时间完全是随机的变化. 比如一个恒星的光度变化,短时间来看后一个时刻的光度和前一个时刻相关,但是长时无关联.
相关函数的有关表述:
关联函数是功率谱在时域上的对应
自关联函数是自身和一段时间后的自身的关联
这正是定义
……
选 a., b..
今天我们讲空间统计 (Spatial Statistics) —— 它和时序统计的区别在于,维数和物理含义不同.
字面上讲,空间统计描述的是空间中一个点集的分布.
- Point Catalogs:比如宇宙网络结构
- Non-Euclidean Space:比如在偏振空间的某种分布
- Non-scalar Fields:比如说速度场、电磁场等等
- Gridded Fields:格点上的空间统计
这些内容主要是宇宙学的角度.
Spatial Clustering Description
最 naïve 的想法就是「数数」. 我们数出每个 bins 里面点的个数,这里的参量是数密度 n≡N/V. 平均数密度:
nˉ≡⟨n⟩=V⟨N⟩
定义 overdensity:
δ≡nˉn−nˉ=⟨N⟩N−⟨N⟩
δ 的符号就表达了某处的数量跟平均值相比是多了还是少了.
CiC (Counts in Cells):数格子,方差为
σV2≡Var(δV)=Var(N)/⟨N⟩2
对于一个随机过程,符合 Poisson 分布,其方差等于均值,所以上面的方差是
σV2=⟨N⟩/⟨N⟩2=1/⟨N⟩=1/(nV)
而 in general,
σV2=nV1+V21∫Vdr1∫Vdr2⋅ξ(∣r1−r2∣)
可以看作是格子之间的方差和格子内部的方差,ξ 被称为两点关联函数.
两点关联函数的含义是,任意找两个在 r1 和 r2 的体积元,它们中可能有点、可能没有点,关联函数描述它们俩之间能够形成多少个点对.
ξ>0 表示关联,ξ=0 表示无关联,ξ<0 表示负相关.
自相关函数:
ξ(r)=⟨δ(r)δ(r+Δr)⟩
为什么不同坐标的 nˉ 是不均匀的?因为不同方向的观测条件实际上是不同的,比如银心方向和另一方向的亮度和干扰就完全不一样,构成一种选择效应.
解决方法是,按照我们已经知道的 mask 和误差分布等等,进行随机大量撒点,因为我们的目标是研究真实的分布和一个随机分布的差别. 这里随机撒点的数量应该要大幅多于真实的 data,为了得到更加精确的结果.
有了随机分布的点 + 真实 data 之后,我们要做的事情是数点对的个数:以某个 data 点为中心,某种半径 r→r+dr 画环形区域,得到这个环形区域内有多少个 data 点,这个数是所谓的 data-data pair;同理,可以以某个 random 点为中心,得到 random-random pair;最后还有一个以 data 点为中心、环形区域内两种点的总个数 data-random pair.
这三种 pair 记为 DD、RR、DR. 对它们做权重估计:
DD=ND(ND−1)/2DD,RR=NR(NR−1)/2RR,DR=NDNRDR
有以下几种 estimator:
"Natural" Estimator (Peebles - Hauser):
ξ^PH=RRDD−1
它对于边界非常敏感,但是比较简单.
Landy - Szalay (LS) Estimator:
ξ^LS=RRDD−2DR+RR
能够处理好边缘的效应,是目前最常用的手段.
Hamilton Estimator:
ξ^Ham=(DR)2DD⋅RR−1
下图就是我们宇宙中关联函数的样子:在小尺度和大尺度呈现出两种不同 index 的幂律,中间的尖峰正是 BAO (重子声学振荡).
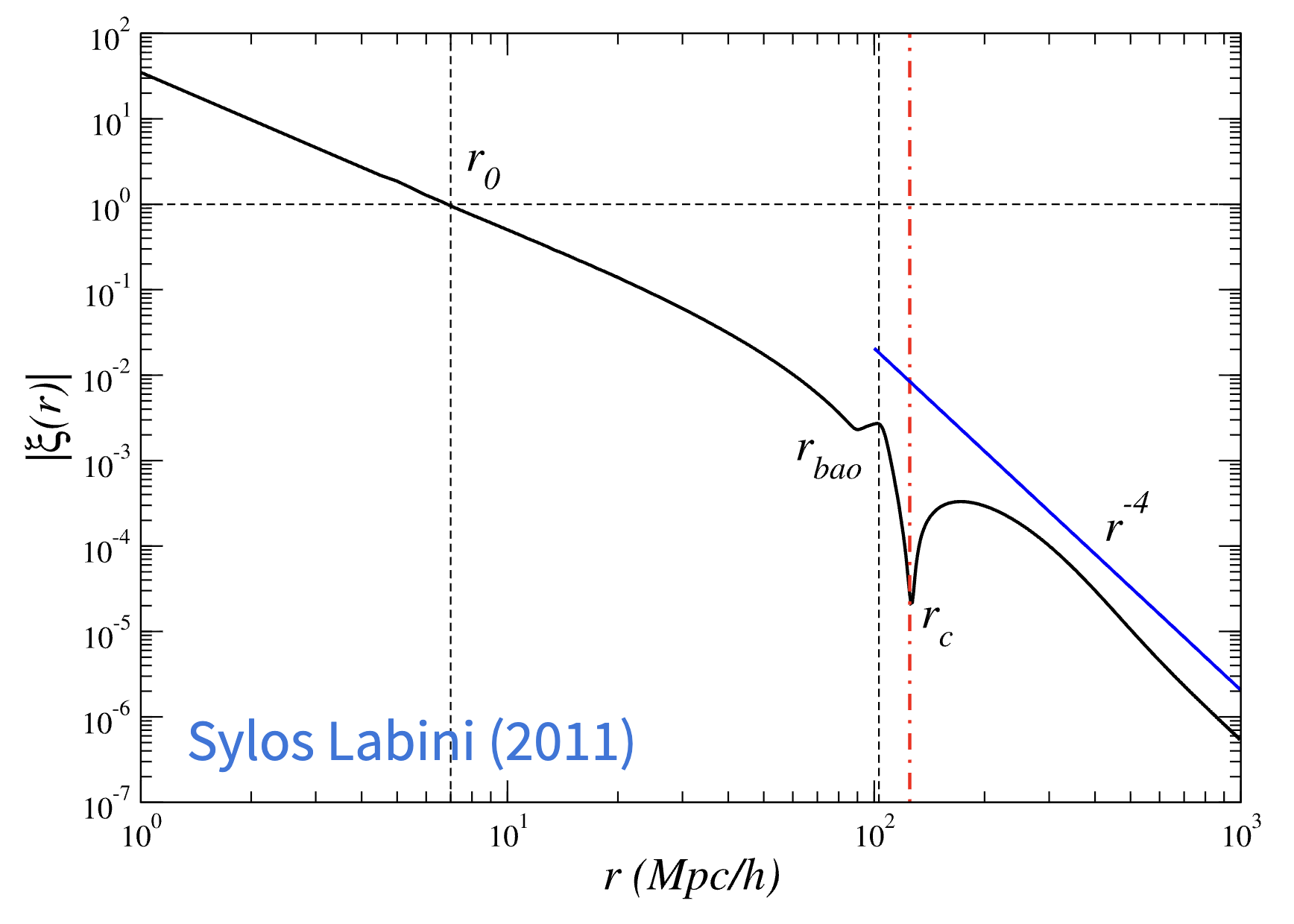
角向的相关函数能够表现各种极矩的性质分布,角向的分布可以用各阶 Legendre 多项式的卷积变换为一维的一条曲线 (数据压缩),不同阶数表达不同极矩,可以在一维曲线上看到二极矩、四极矩等等分布:
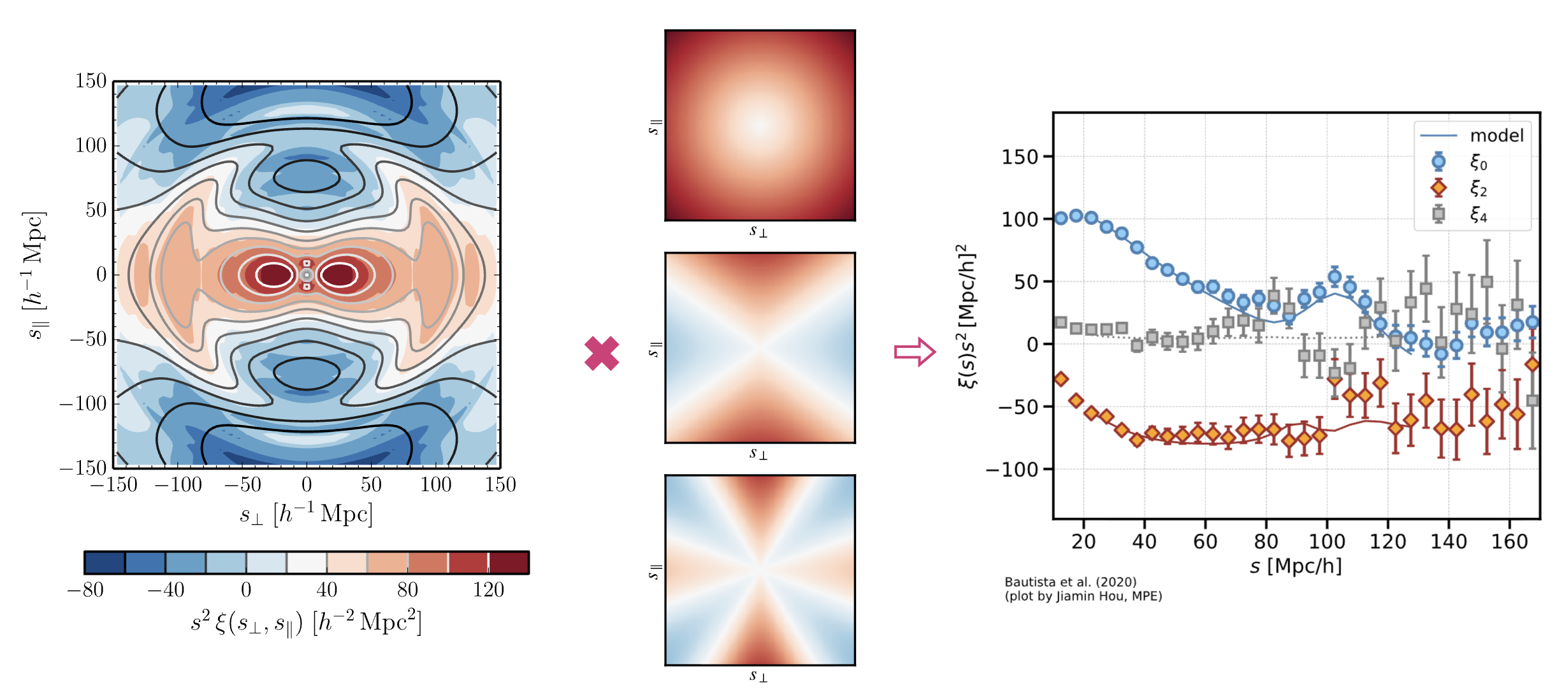
很多关联函数的变种:
- Marked 2PCF (2 particle correlation function):
M(r)=1+ξ(r)1+W(r)
加入权重 W(r) 的关联函数,将权重所包含的物理信息也加入了整体的关联函数中,得到更丰富的信息.
- 星系的速度场关联函数 / 星系的形变关联函数:
前者是矢量场的关联、后者是张量场的关联,这些数据并不是点,但是其关联函数也有非常好的信息. 另外类似的还有 Lyman-α forest 关联等等.
代码工具:
老师自己写的 (全世界数 pair 最快的代码!):
Fast Correlation Function Calculator (FCFC): Zhao et al. (2023)
Clustering Models
下面我们来说我们到底从关联函数的空间统计中得到了什么内涵.
一百年前,人们提出了分层的宇宙结构模型 —— 这个模型到现在仍然不过时,我们确实在宇宙中观察到了超星系团 - 星系团 - 星系 - 卫星星系 - …… 的结构.
- Neyman-Scott processes (1953):
- Galaxy clusters:呈现 Poisson 分布的形式
- Galaxies:在 clusters 中间以 Gaussian 分布.
- 在上述模型基础上,提出了 Halo Model:ξ2halo+ξ1halo.
模拟步骤是,先随机撒 clusters,然后在 clusters 中间随机撒 galaxies. 因为是完全随机撒 clusters,那么 halo 的关联函数 ξ2halo=0. 而 ξ1halo 应该取决于我们在 halo 中怎样分布星系,
ξ1halo(r)∝∫ρ(x)ρ(x+r)d3x
得到的结果应该是:小尺度上关联为幂律 ∝r−1,大尺度上关联为 0.
当然实测的数据和模拟数据不同,实际上 2 halo term 是对暗物质分布的一种「采样」,也就是用星系的分布来表现暗物质的分布. 所以我们在上面模拟的 toy model 中得到的结果部分正确 —— 最大尺度上 2 halo term 为零;但是在中等尺度上 (超过 BAO 之后) 并不是完全正确,这个尺度上还有暗物质的一些有特征的分布.
在早期宇宙中我们可以通过 CMB 的温度分布来找到暗物质分布,这正是我们要在现在找到中等尺度暗物质 2 halo 关联函数的原因.
对于一个 Gaussian 随机场,协方差矩阵在某种程度上就是关联函数:
M=⟨δ(xi)δ(xj)⟩
定义功率谱为关联函数的 Fourier 变换,
P(k)=∫ξ(r)eik⋅rd3r,ξ(r)=∫(2π)3d3kP(k)e−ik⋅r
这样的角度看,协方差矩阵:
Mij^=∫d3x⋅ei(ki−kj)⋅x⋅P(kj)
这是对角化的一个协方差矩阵.
Gaussian Random Fields:给出一个 power law 的功率谱,可以对应地画出相应的随机场,实际上 CMB 非常接近于一个 P(k)∝k−1 的随机场.
代码实现:
def generate_grf(power_spectrum, Lbox=100, Ngrid=128, seed=42):
"""Generate a Gaussian random field given a power spectrum"""
rng = np.random.default_rng(seed)
# Generate the white noise field
noise = rng.normal(size=(Ngrid, Ngrid, Ngrid))
noise_k = np.fft.fftn(noise)
kx = np.fft.fftfreq(Ngrid, d=Lbox/Ngrid) * 2 * np.pi
k = np.sqrt(np.add.outer(np.add.outer(kx**2, kx**2), kx**2))
# Apply power spectrum
Pk = np.zeros_like(k)
mask = k > 0
Pk[mask] = power_spectrum(k[mask])
delta_k = np.sqrt(Pk) * noise_k
# Inverse FFT to get real-space field
delta = np.fft.ifftn(delta_k).real
return delta
grf = generate_grf(lambda k: k**-3) # Example: power-law P(k)如何把离散的分布放到一个比较规矩的格子上?(FFT 要求均匀的采样)
- NGP (Nearest - Grid - Point):分配到最近的格点
- Cloud-in-Cell:按照距离四个近邻格点的距离分配权重,把一个格点分成四份到四个最近格点上.
分配完之后,我们可以做 FFT 得到功率谱 P(k). 下面是结果:
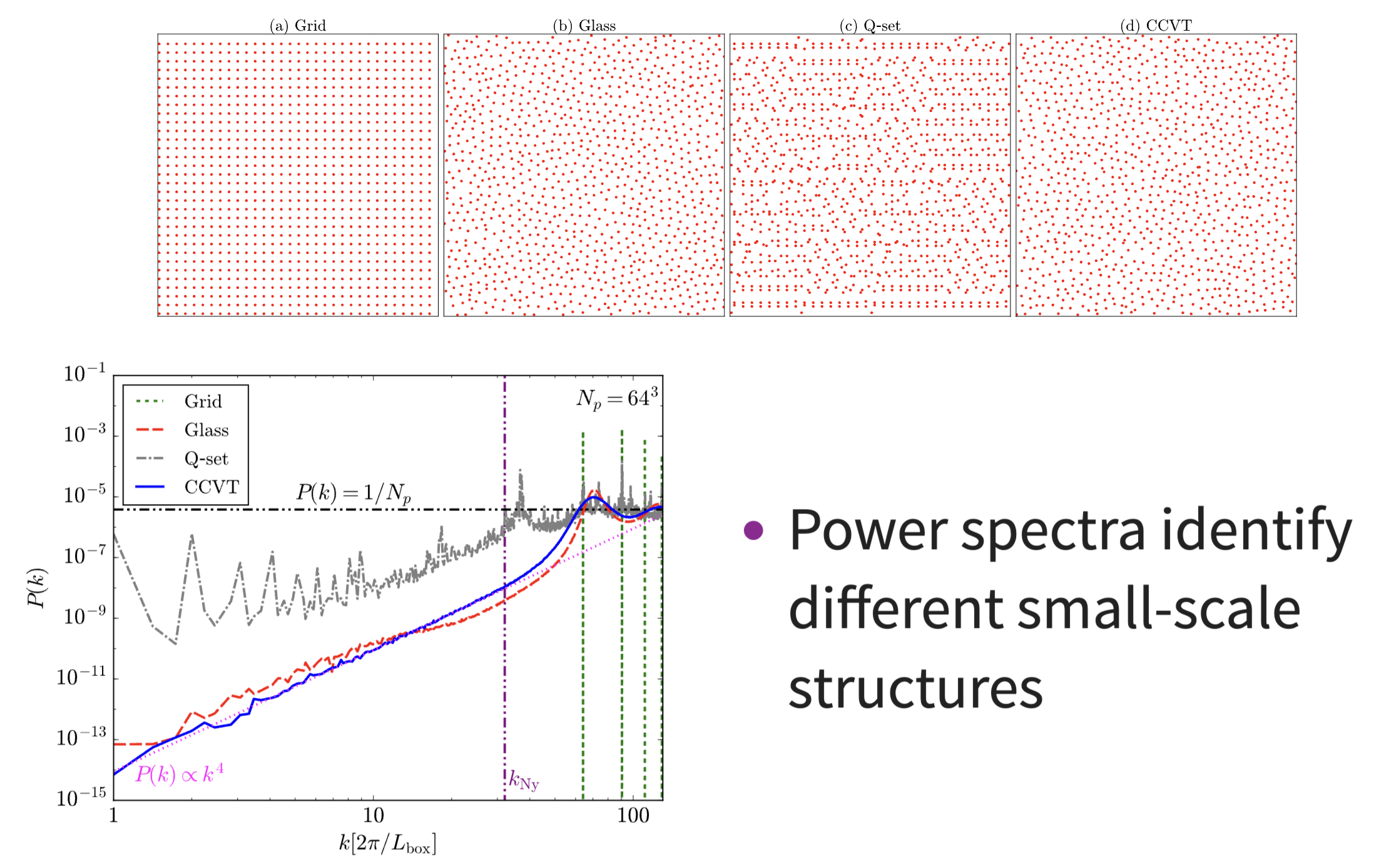
下面是宇宙学上实际的功率谱 (非常漂亮的两段幂律):
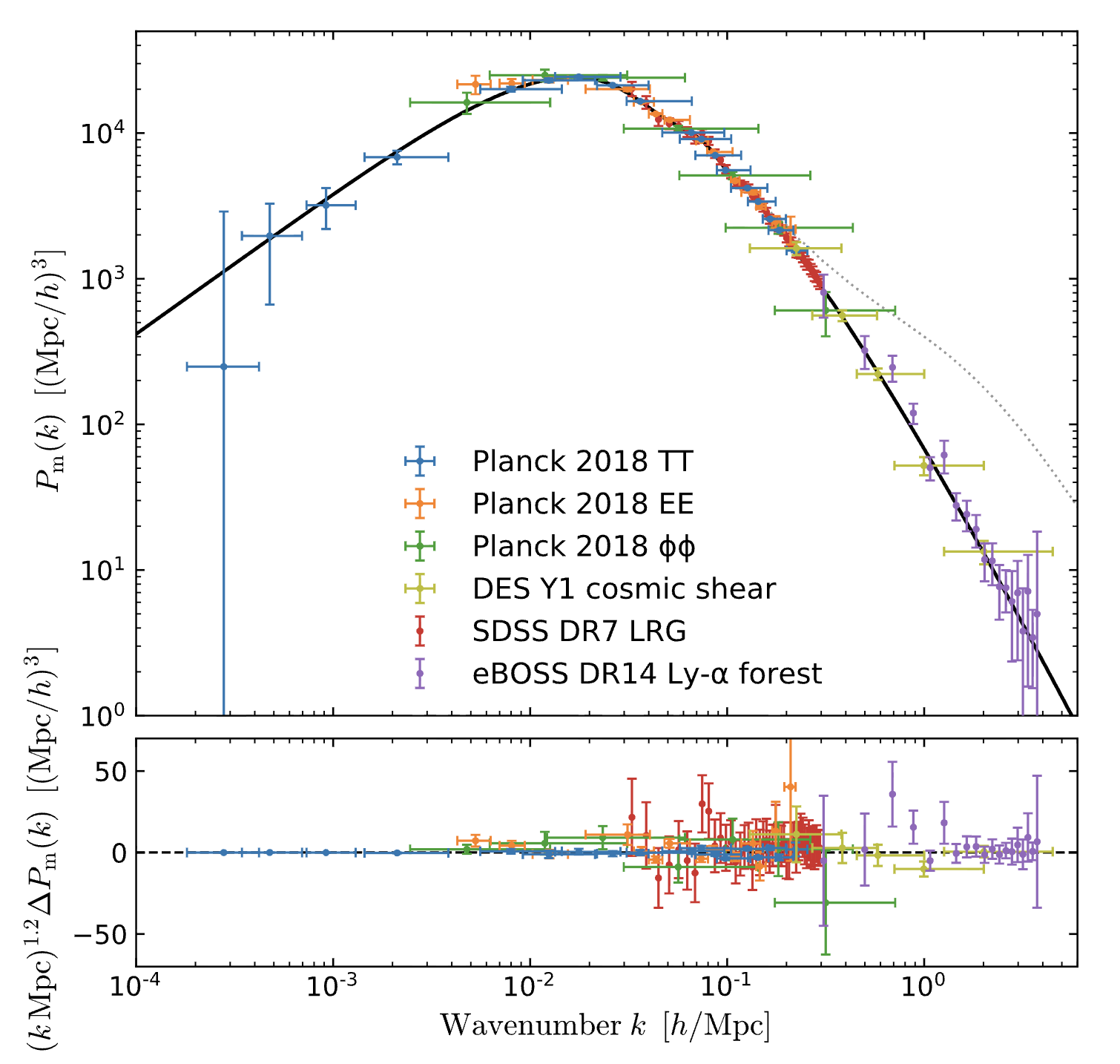
Beyond 2 Point Statistics
三点相关:把离散的点三角化,使得整体看起来是连续的分布 —— 这在地理测绘上和计算机图形学都比较有效,并且可以简单地扩展到更高维度.
在宇宙学上,我们在模拟的星系分布之上想要展示出背后的暗物质分布,实际上就是在这些星系点之间做三角化插值,然后获得一个更加连续的「暗物质分布」.
机器学习兴起之后,有时候可以抛弃传统的点估计方法,而是对整个场进行拟合.
Video: Mapping the Universe
看视频 ing.
在 THU,我们正在做更有野心的事情 —— MUST.
更新日志
2025/12/18 16:20
查看所有更新日志
2d661-feat(note): add note于
