提示

Quizzes

1. 选出可以被定性为 density estimation 的问题：

   1. 为 Hubble 常数拟合一个直线

   2. 估计 gamma 射线暴的持续时间分布

   3. 在巡天数据中估计变星的比例

      这实际上是一个「参数估计」.

   4. 确定观测到的星系在体积中的计数是更加符合 Poisson 分布还是负二项分布

      这实际上是一个「模型选择」.

   5. 估计巡天数据中的星系颜色分布

   6. 估计一串模拟数据中粒子的密度分布

   选择 b., e., f..

2. 关于直方图的说法正确的是？

   1. 改变直方图第一个 bin 的起点，直方图的形状会变

   2. 用更多的 bin 总是能够获得更好的估计

      bin 更多，对噪声更加敏感，不利于提取有效信息.

   3. 用等宽的直方图，可能会错过一些 feature，也可能会在数据少的地方浪费 bin.

   4. Bayesian Blocks 是一个自适应取 bin 宽度的方法.

   选择 a., c., d..

3. 简单描述一下什么是 KDE (Kernel Density Estimation)，并简述其工作原理.

   就是在每个数据点上面放一个 kernel 函数，整体加起来形成一个连续的分布.

   注意

   每个 kernel 的宽度称为「带宽」，这是一个关键的量.

4. 关于 KDE 的说法正确的是？

   1. Kernel 的形状比带宽更加关键 (对于结果的影响更大)

   2. 带宽控制密度估计的平滑程度

      简单地用极限思想来思考，如果带宽无限，最后会变成一个 uniform；反之，如果是一个 $\delta$ 函数形状的 kernel，最后会极为不连续.

   3. Cross-validation 能够用来选择一个合适的带宽

      我们只要知道有这个方法就行了……这门课的后半主要是讲概念，大家了解一个「搜索用的关键词」就算是有收获.

   4. 数据有噪声时，KDE 不能工作

      噪声污染数据的过程和 KDE 处理数据的过程，都是一个卷积，因此如果我们知道了噪声的生成方式，可以把这样的分布并入到 kernel 里面，最后能够得到极为真实的数据，反而在有噪声的情况下 KDE 工作得很好.

   选择 b., c..

5. 关于 $k$ - NN 的说法正确的是？

   1. $k$ - NN 估计的是每个点处 $k$ 个邻居的密度
   2. $k$ 的作用类似 KDE 中的带宽
   3. 可以用 cross - validation 确定一个合适的 $k$
   4. 相较于 KDE，好处在于 $k$ - NN 的「带宽」取决于当地的邻居分布，是自适应的，而不是固定的带宽

   选择 a., b., c., d..

6. 关于神经网络的说法正确的是？

   1. 是用神经网络学习复杂的概率分布函数
   2. 这个方法在高维下优于 KDE
   3. 可以处理任意维度
   4. ……

   选择 a., b..

• Clustering (聚类)：将相近的数据分组，使得组内数据接近，组间数据相差较远.

  这是一种 unsupervised learning，我们暂时还什么都不知道.

• Classification (分类)：我们已经有了 clusters，获得新的数据之后要把它们归类到某一类中去.

  和上面相比，这是 supervised learning，我们已经预先有了对 clusters 有哪些的知识，进行下一步的工作.

这两个概念看起来非常简单，但是是科学研究的基本方法；而且因为天文观测数据相对来说非常少，所以显得尤为重要.

一个例子是恒星分类，最早的天文学家们用英文字母来分类不同光谱类型的恒星，但是后来发现光谱表征了恒星的温度，按照温度排序由高到低是 Q, B, A, F, G, K, M... 但是这个序列和原来的顺序完全不一样了，很多历史的因素导致我们难以记住这些分类规则.

提示

实际上还是有个规则的：Oh Be A Fine Girl Kiss Me (这是一个顺口溜)

另一个例子是按照形态分类不同星系，有所谓的 Hubble's Galaxy Classification Scheme，它们实际上和星系的演化过程有关系.

分类的好处是，我们可以只具体研究一类，同时可以认为相似的类之间具有相近的起源或者演化过程、或者找到类之间的演化过程；另外，我们可以容易地发现异常的个体，或者预测新发现的个体应该具有何种和之前一样的共性，指导未来的观测.

Clustering

K - means

最简单的方法叫做 $K$ - means 方法：

把数据分成 $K$ 个类，类的均值序列为 $\{\mu_k\}_{k=1}^K$，要求列内部的方差尽可能小：

$$\min_{\{C_k\}}\sum_{k=1}^K\sum_{x\in C_k}\|x-\mu_k\|^2$$

具体过程是，先确定 $K$，然后扔 $K$ 个重心在图上，把每一个点归类到离它最近的那个重心的类别去. 归类一次之后，把两类的重心算出来，然后用两个新的重心再进行一次演化，之后不断迭代，等重心位置都不再变化，就能确定最后的分类.

最后的结果有一个专有的名字 —— Voronoi Diagram，它是一种划分全空间的方法，能够保证全空间的每一个区域的任何一个点都距离该区域的重心最近，而不可能离其他区域的重心更近.

这种方法的缺点：

• 对重心初值敏感.

• 对 outlier 敏感.

• 对于坐标的 scale 敏感.

  举个例子，如果 $y$ 坐标的标度很大，那么 $\sum\|x-\mu_k\|^2$ 里面就全是这个坐标轴的数据.

Hierarchical Clustering

更好的方法是 Hierarchical Clustering.

最开始我们认为每一个数据都是一个类，然后 merge 最相近的两个点，是否 merge 的判据有很多种，比如：

• Single linkage: $d_{\min}(C_k,C_{k'}) = \underset{x\in C_k,x\in C_{k'}}\min\|x-x'\|$.
• Complete linkage: $d_{\max}(C_k,C_{k'}) = \underset{x\in C_k,x\in C_{k'}}\max\|x-x'\|$.
• ……

一个一个生长上去，clusters 会变得越来越少，把每一次的高度画在这样的图中：

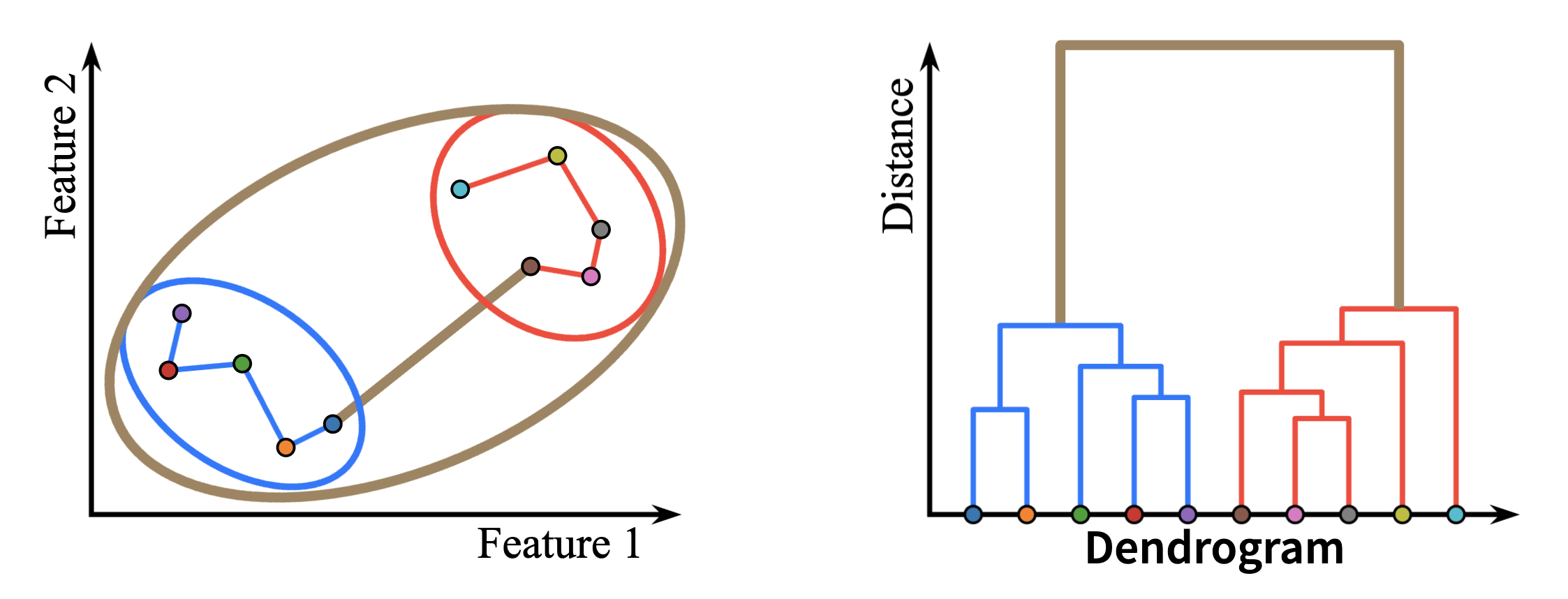
那么只要找到落差最大的两次生长，把这个「树」切断，就得到了最佳的分类.

如果是 single linkage，那么我们叫它「朋友的朋友」算法；同时我们在图中会连接所有的点，这种图在计算几何中被称为最小生成树，它是连接各点的最短路径.

如果用 complete linkage，那么会得到非常 compact clusters.

/Example/

这个方法可以在 SDSS 巡天数据中找到星系团；另外，在 1998 年的一篇文章中，人们分析 $\gamma$ 射线暴，找到了除了短暴和长暴之外的另外两种射线暴.

DBSCAN

第三种方法：DBSCAN (Density - Based Spatial Clustering of Applications with Noise).

两个参数：

• $\varepsilon$：两个点成为邻居的最大距离
• $m$：成为一个 core 的最小点数 (包含自身)

对于一个点，先找到其所有邻居，如果少于 $m$ 那么标记为噪声；反之定义一个 cluster，将这个点作为一个 core. 然后检查邻居，找到「朋友的朋友」. 如果是在 core 的邻域内的噪声，被标记为 border (边缘点).

这个方法的灵活度更大，取决于局域的密度，自适应地划分 clusters.

/Example/

一个例子是 Gaia 卫星的银河系观测数据，找到星团.

因为星团可能被潮汐力撕碎，相距很远的星体可能属于同一个星团，所以要引入光谱等额外参数，而且还无法在一开始确定有几个 clusters. 这时候非常适合用 DBSCAN.

所有上面讲到的方法都可以用简短的代码来实现：

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN
# Create test data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(300, centers=centers, cluster_std=0.4)

# K-Means clustering
kmeans = KMeans(n_clusters=3)
label_kmeans = kmeans.fit_predict(X)

# Hierarchical clustering
hie_model = AgglomerativeClustering(linkage='single')
hie_model.fit(X)
label_hie = hie_model.labels_

# DBSCAN clustering
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
label_db = db.labels_

Classification

已经分好 clusters，现在我们要把新的数据归类了. 考虑 $\{x\}$ 中有 $n$ 个点，每个有 $m$ 个 feature，第 $i$ 个点的第 $j$ 个 feature 表达为 $x^j_i$.

标签序列为 $\{y_i\}$，Bayes Theorem：

$$p(y_k|\vec{x}_i)=\frac{p(\vec{x}_i|y_k)p(y_k)}{\displaystyle{\sum_{j=1}^lp(\vec{x}_i|y_j)p(y_j)}}$$

用下面两个量来考察我们的分类是否好：

• Completeness：

  $$\text{completeness} = \frac{\text{true positives}}{\text{true positives} + \text{false negatives}}$$

• Contamination (被噪声的污染程度)：

  $$\text{Contamination} = \frac{\text{false positives}}{\text{true positives} + \text{false positives}}$$

Naïve Bayes

$$p(x^1,x^2,\cdots,x^m|y_k)=\prod_{j=1}^m p(x^j|y_k)$$

于是，

$$p(y_k|x^1,x^2,\cdots,x^m) \propto p(y_k)\prod_{j=1}^mp(x^j|y_k)$$

这个方法是最小化下面的量：

$$\hat{y}=\arg\max_{y_k}p(y_k)\prod_{j=1}^mp(x^j|y_k)$$

/Example/

天鹅座 RR 变星：光变曲线的周期和绝对亮度有关系，所以观测到周期就能确定其绝对亮度，再和相对亮度对比就可以测距. 我们要找出哪些是这样的变星.

但是结果的范围并不是很好.

一个更优化的思路是引入联合 Gauss 分布. 但是问题在于，这里的自由参数太多了，整个协方差矩阵都是自由的.

k - NN Classifier

通过「邻居投票」的方式来归类，同时按照邻居的距离来算投票的权重.

特征是：没有训练集、对 outliers 和不同 feature 的 scale 敏感...

SVM

画一条直线边界，让两个 clusters 距离这歌边界尽可能远 (所谓「最大二乘法」)

扩展是多核 SVM (KSVM, Kernel SVM)，把数据点升维，边界变为高维平面，投影回来就不再是直线，而是一个复杂的曲线边界.

这种方法的 completeness 极高，但是引入了很多噪声污染.

Decision Tree

决策树，用熵来算应该如何「切割」数据，计算切割之后的 information gain：

$$\text{IG}(x,y)=H(x)-\sum\frac{|x_v|}{|x|}H(x_v)$$

这种方式的参数实际上只有「切几刀」.

Dimension Reduction

有时候我们不希望有很多维度，因为维度之间可能存在相关性，没必要引入太多维度；同时会增大计算难度. 我们希望在不破坏重要结构的情况下降低数据集的维度.

PCA

Principle Component Analysis. 找到各个维度之间的重要性排序，去寻找一个平面平行于「最重要的方向」，把所有数据投影到这个平面上面.

SOM

Self - Organizing Map (自组织映射)：比上面那个方法更加现代，利用神经网络，把任意维度降低到二维.

这其中的映射非常复杂 (毕竟基于神经网络).

Exercise: Iris Classification

做鸢尾花的分类，这是一个经典的验证分类方法好坏的数据集.

有三种鸢尾花，四个 feature：萼片长度、萼片宽度、花瓣长度、花瓣宽度. 这个数据集是在 python 库里面自带的 (因为太经典了).

选择自己喜欢的分类方式来做分类.

利用 nearest neighbour 的例子：

from sklearn import datasets
import matplotlib.pyplot as plt

iris = datasets.load_iris()

# Take the first two features (sepal length and width)
X = iris.data[:, :2]
y = iris.target

plt.scatter(X[:, 0], X[:, 1], c=y, cmap='jet', s=20);

from sklearn.neighbors import NearestCentroid
import numpy as np

clf = NearestCentroid()
clf.fit(X, y)
y_pred = clf.predict(X)

plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='jet', s=20);

更新日志

2025/11/20 15:18

查看所有更新日志

• bd7b8-feat(note): add as note于 2025/11/20

版权所有

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)