菲兹克斯喵

外观

请我喝杯奶茶→

Lesson 1 Introduction

复制页面

约 3409 字大约 11 分钟

2025-09-18

Introduction

有必要分享一下开这门课的目的：统计课应该是每一位成熟的大学生学习的，因为教的是「逻辑」. 当然统计系也会开统计课，不同领域都会用到统计相关的方法，毕竟是一种基础的工具. 在学习统计时，要把它和它的应用结合在一起，才会不至于太枯燥.

统计从诞生之初就和天文相关，到目前为止还有很强的交叉性.

这门课程的目的：

  • 了解「数据」(或者说经验) 如何转变为「知识」.

    比如北京每年都下雨，那么明年大概率也会下雨.

  • 作假设和决策：忠实地知道自己知道什么、不知道什么，量化这样的判断.

  • 天文相关的数据处理：通常，这是不完备的 (一个天体很暗，看不到) 并且有噪声的.

    对比自己的生活，也是「不完备的」，很多时候我们并不了解真正的科研或者生活中发生的一些事情，观察是很有限的，要在这样的情况下做出合理的决策.

  • 解决科研和生活中的问题，学会分析问题解决问题的方法.

  • 一些批判性思维与技能：作出可读的图、清晰的解释、合理的总结.

希望大家能够学会：

  • 把一个具体的问题变成一个统计的问题；

  • 评估和理解所谓的「不确定性」，不管是生活中的还是研究中的；

  • 面对不同的问题，能够选择合适的不同方法；

    如果大家上过统计相关的课程，可能会发现不同的人对不同的问题会给出很多花样繁多的方法，方法一多就不知道该用什么. 我们需要了解方法的选择.

  • 一些简单的代码能力；

  • 学到的知识指导生活和工作.

后面的每一节课都会有具体的问题，这是一个问题驱动的课堂；另外，我们会尽量少地使用数学，而是使用生活常识来试图解决问题；在课堂上利用的方法，都会是实际科研中能够应用得上的方法，并讨论为什么使用这样的方法，加深对这些东西的印象. 最后在课堂上希望大家能够做出能够跑起来的代码.

LectureDateTopic
012025.09.18Introduction
022025.09.25Probability Theory
032025.09.28Probability Distribution Functions
042025.10.09Parameter Estimation
052025.10.16Model Selection
062025.10.23Multivariate Analysis
072025.10.30Regression
082025.11.06Nonparametric Statistics
092025.11.13Density Estimation
102025.11.20Clustering & Classification
112025.11.27Censored & Truncated Data
122025.12.04Time Series Analysis
132025.12.11Guest Lecture: Al for astronomy
142025.12.18Spatial Statistics
152025.12.25Project Report

(前面几节课可能有数学，后面基本是将问题转化为代码的能力)

成绩评定：

  • 10%10\% 是课堂参与；

  • 40%40\% 是作业，每次作业有三个题，第一个是上课解决的，第二个是难度相当的，第三个是更加困难一点的问题；迟交扣分，deadline 是 2 周；

    希望大家把设备带到课堂上.

  • 50%50\% 是大作业，给大家 4∼54\sim5 个小课题，数据来源都是真实的前沿数据，当然会设定边界使得这个问题可做. 另外小组成员看到的问题方面是不同的，所以每个人的报告都会有差异；

  • 5%5\% 的加分来自于用英文写报告.

上学期经验来讲，会用 AI 的话一般两小时能够完成作业.

参考书：

  • Statistics, Data Mining, and Machine Learning in Astronomy (A Practical Python Guide for the Analysis of Survey Data), Ivezić, et al. 这本书甚至单独写了一个 py 库；

    这本书建议有志于研究天文的学生读.

  • Data Analysis (A Bayesian Tutorial), Sivia & Skilling

    这是一本比较数学的书，可以当作一种「字典」.

  • Practical Statistics for Astronomers, Wall & Jenkins

  • Modern Statistical Methods for Astronomy With R Applications, Feigelson & Babu

  • Probability Theory (The Logic of Science), Jaynes

  • Numerical Recipes (The Art of Scientific Computing), Press, et al.

FAQs：

  • "No astro background?"

    没有必要，当然最后几节课可能稍微有一点联系.

  • "Prior knowledge?"

    微积分和线性代数，剩下的只有一个有逻辑思维的大脑.

  • "Math?"

    主要是逻辑推理.

  • "Coding skill?"

    没有代码能力的要求.

  • "AI?"

    要理解 AI 说了什么.

Lead - In

The true logic of this world is the calculus of probalility.

—— Maxwell

为什么要在天文中用统计？

在所有领域都有统计，不只是天文.

Deductive logic (演绎逻辑) v.s. Pausible reasoning (合情推理)

↑\uparrow 这是我们对这个世界的认识模式.

演绎逻辑：

A⇒BA\Rightarrow B (已知 AA 为真，BB 为真)

All men are mortal. & Socrates is a man.

⇒\Rightarrow Socrates is mortal.

这时，同一个 cause 可以推出很多不同的 outcome.

合情推理：

A⇒BA\Rightarrow B，现在我知道 BB 真，那么 AA 真的可能性变大；如果知道 AA 假，那么 BB 假的可能性变大.

下雨地面会湿. & 地面是湿的.

⇒\Rightarrow 刚刚应该下了雨.

这样的推理方式适用于一些 causes 很多、outcomes 也很多的情况；它的三段论更加弱.

一副图片：一个写着吕洞宾的月饼被咬了一口. 看到这样的图片，你的推理能被怎样描述为三段论？

作一个非常强的前提：狗和吕洞宾在一起，吕洞宾会被咬. 现在我已知月饼 (吕洞宾) 被咬了. 那么弱三段论的结果应该得到：拿着这个月饼的人是狗.

这个例子是明显的合情推理，但是我们在日常可能会遇到不少判断不清是何种推理的情况，需要做出清晰的认识.

提示

/Group discussion/ most fundamental difference between deductive & plausible reasoning

  1. Direction of reasoning
  2. Amount of prior knowledge
  3. Completeness of information
  4. Ability to make predictions
  5. Certainty of conclusions

其实最本质的区别在于，是从果到因推理还是从因到果推理，也就是我们知晓的信息是否完备，这就是我们需要在天文中做统计的原因.

在演绎推理的过程中，我们只是在合理往后推断；但是合情推理中，我们需要关心证据的强度. 这对应两种问题，前者是利用一个被认为是正确的理论来导出合理的结果；后者则是用不完备的信息来反推可能成立的理论.

将上面的合情推理定量化的方式，就是统计.

典型的天文数据：被引力透镜扭曲、遥远的位置产生光削弱、不同天体带来的噪声、…… 为了能够看到尽可能多的东西，我们一般会将仪器使用到极限，这时接收到的光子数已经非常少，噪声极大；同时我们没办法做「重复实验」，不能让宇宙重新演化一遍，超新星爆发了就已经爆发了，宇宙当前的演化是这样，早期的量子涨落也没办法重来；同时暗的源永远比亮的源多，做观测时突然有一个星链的卫星飞过，数据就不完备了；前景的污染强烈，人造灯光和大气层等等造成了很多杂音.

⟹\Longrightarrow 天文的数据是极度不完备的！

所以我们在天文中必须学会统计和建模，判断哪些理论是对的、下一步该进行什么样的观测.

"Science, and in particular Modern Astronomy and Astrophysics, is impossible without knowledge of probability and statistics."

—— John Peacock

什么是概率？

从历史的角度，来看看不同的人对概率有什么样的看法；概率的不同概念...

1713 年，Jakob Bernoulli 逐步开始建立起统计学，提出了「Principle of Insufficient Reason」，也就是当你无法区分 NN 个事件中哪个更有可能，则它们的概率相等，都是 1/N1/N.

1763 年，Thomas Bayes 想到，通过我们现有的知识可以更新我们对概率的认识，比如如果我们在上面 Bernoulli 的情况中多了解了一些证据支持某一个事件，则这个事件的概率变高.

1795 年，Gauss 建立了 Gauss 分布和最小二乘法. 这些方法就是用来处理天文数据的.

1820 年，Laplace 自己重新发现了 Bayes 原理，并将功劳归功于之前的 Bayes. 和 Gauss 一样，他开始用这些原理统计天文数据.

1850's，上面的理论在很长时间内被忽视了，取而代之的是 frequentists (频率学家们). 这是因为之前我们的「均等概率假说」这样的概念听起来有很大的主观性，难道我们了解的知识会影响事件发生的概率吗？同时，Bayes 原理对计算的要求天然就很高，一个简单的问题可能就会让计算机算不少时间，何况那时没有计算机.

1920's，电子计算机出现、数据量大量增加后，Bayes 原理重新开始发挥它的作用.

Frequentists v.s. Bayesian：Laplace 利用当时的轨道数据来推算土星的质量可能值，得到了一个质量 - 概率图. 但是这个概率意味着什么？土星的质量会变吗？

变化的并不是土星的质量本身，而是我们对这个质量值的信任程度.

但是频率学家认为，土星的质量是一个常数，你的信念和我的信念不一样，那该用什么样的概率呢？他们认为 Bayes 学派的概率并不客观，真正客观的是长期的实验得到的大量数据中出现的频率.

但是土星质量用频率学家的观点似乎没办法解决. 他们想到的方法是，认为观测数据有随机的噪声，测量的是噪声的概率. 但是这样就会导致不同的问题需要不同的噪声分析，频率学家的工具箱变得极为复杂，对白噪声、红噪声等等要分开分析.

这时候不得不问：在没办法重复实验时，怎么预测？如果只有随机变量才有概率，那么什么是「随机变量」？如果测量误差有概率，那么测量误差真的是「随机变量」吗？

提示

/Group discussion/ What are real randoms?

  1. Flipping a fair coin
  2. Numerical random number generator
  3. Dynamics of chaotic systems (e.g., three-body problem)
  4. State of elementary particles

大家没有共识，意味着大家对「随机」的认识并不一样.

大家都觉得 B 不对，但是假设我要用 Ment-Carlo 来计算 π\pi，如果数据不随机，我就算不对 π\pi；但是在电脑里生成伪随机数来算，可以得到对的结果.

对于 D，电脑里那么多量子效应，但是我们会选择相信电脑给出的结果，这是随机吗？

是否随机，取决于我们对这个事件了解的多少，以及和我们正在做的这个问题的联系. 比如让小朋友做算数，得到的结果就像一个随机分布，这就是因为掌握的信息不够. 因此，按照 Bayes 的观念，一个事情只要对我们研究的问题没有影响，就能认为这是随机的.

也就是说，虽然 Bayes 原理有主观性，但是我们承认主观性，对我们来说概率还是基于手头的知识和数据. 在这个程度上，我们永远无法证明一个理论是正确的，因为信息永远不完备，不管是力学混沌系统还是抛硬币，我们只要对数据知道得任意精确、有足够强的算力，就能计算出结果.

统计和天文的关系

这两者很多时候是共同发展的，不管是早期、还是最近三十年以来. 老师个人认为，所有的天文都是在玩统计.

  • Laplace & Gauss 的时代 大家用 Bayes 观点处理谷神星、土星等等天文问题

  • frequentists 的时代

    因为 Bayes 算法很难计算，两者逐渐脱节

  • 20 世纪初

    二者又开始结合

  • 早期的人工智能 (和大语言模型不一样)

现在面临的问题是数据量越来越大 (PB/week\text{PB/week} 量级)、模型越来越精细，和计算的结合也更加紧密，所以需求更好的统计方法和算法.

这节课最终的目的：就是理解这样的图片 ↓\downarrow

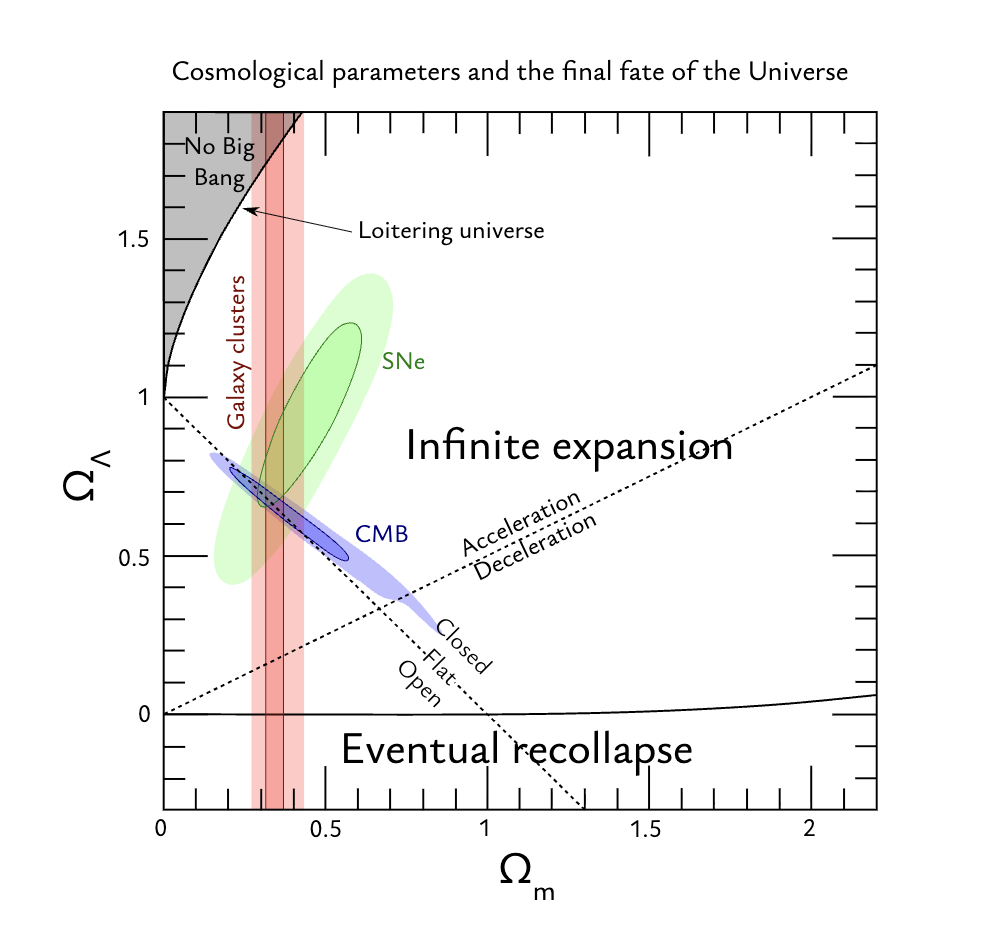
后面我们会讲简单的统计，后半学期我们将了解很多更加细节的方法，也会见到出现在公开文章中的错误例子 (混用弱三段论和强三段论).

Python Tutorial

现在开始教大家简单的 python 脚本，课程最后的作业也会上交一个 Jupyter Notebook.

# 导入需要的包
import numpy as np
import matplotlib.pyplot as plt

# 在 Jupyter Notebook 中更方便地画图
%matplotlib inline

# 固定种子和生成随机数
N = 10000
seed = 12
rng = np.random.default_rng(seed)
data = rng.random(N)

# 画直方图
plt.hist(data, bins=20, range=(0, 1));

作业会在 Jupyter 服务器上布置.

更新日志

2026/9/9 05:47
查看所有更新日志
  • d6df0-build(theme): theme update于
  • c3099-build(theme): update theme于
  • f85b5-build(theme): update theme to rc-168于
  • 00730-feat(note): add astro-statistic于

版权归属：physnya

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)