Feynman 物理学讲义 - Vol.III 札记 17

2024-12-25

这节课有巧克力吃(╹ڡ╹ ).

---

两个铁球为什么同时落地？（等效原理）

历史上，Feynman 在当年上课时，同时也在做量子引力的工作，他希望舍弃所有 Einstein 所做过的假设，没有几何、没有广义协变性，从引力子是一个 spin - 2 的无质量粒子出发来找到全部的理论.

他没有完全成功，但是同时代的 Weinberg 对“两个铁球为什么同时落地？”这一问题做出了更好的解释.

我们第一次知道这个问题实际上是在语文书里，但是问物理研究工作者，不一定所有人都能很好的解释这个现象 —— 实际上，Einstein 的理论中，等效原理完全是一条假设.

现在我们拥有的事实是：

1. 引力子 massless，spin - 2
2. Lorentz 不变性.

这节课我们将从这个问题入手，复习我们在这门课中学到的常识：

1. 经典物理中的 Green 函数（这其实是 Feynman 物理学讲义 Vol.II 的内容）
2. 双缝干涉 $\Longrightarrow$ Feynman 图
3. 能动量守恒，质壳条件（狭义相对论）
4. 无质量粒子的极化
5. Weinberg's soft theorem（1964）

---

Green 函数

d’Alembert 算子，定义为

$$\Box A_\mu=(-\frac{\partial^2}{\partial t^2}+\nabla^2)A_\mu$$

通常的 d’Alembert 方程是$\Box\phi=0$. 问：由任意的源$J(x)$产生的$\phi(x)=$？这时候的方程是$\Box\phi(x)=J(x)$，引入 Green 函数：

$$\Box_xG(x,y)=\delta(x-y)$$

则

$$\phi(x)=\int\text{d}y\cdot G(x,y)J(y)$$

是线性叠加. 为了解出$G(x,y)$，我们考虑作用一个 d’Alembert 算子的“逆”，得到

$$G(x,y)=\Box_x^{-1}\delta(x-y)$$

做四维的 Fourier 变换，$\int\text{d}^4x e^{-\text{i}k\cdot x}f(x,y)$，其中的$k\cdot x$是四维协变的量，$=-k^0x^0+\vec{k}\cdot\vec{x}$.

变换之后应该得到$G(x,y)\to G(k^\mu)$，$\delta(x-y)\to1$，$\Box_x\to-k^\mu k_\mu=E^2-\vec{k}^2$.

于是，Green 函数实际上是质壳条件的倒数，也就是

$$G(k^\mu)\sim\frac{1}{E^2-\vec{k}^2}$$

物理意义是，$G\sim1/r$，当质量不为零时，得到一个 Yukawa 势，动量空间中对应一个

$$G=\frac{1}{E^2-\vec{k}^2-m^2}$$

双缝干涉

实际上这就是 Feynman 图，用量子力学的基本原理来解释粒子的散射. 每画一个 Feynman 图，就是在计算这个图对应过程的概率幅.

在做 Feynman 图时，应用狭义相对论的基本原理，我们会发现一些有意思的事情.

/Example/

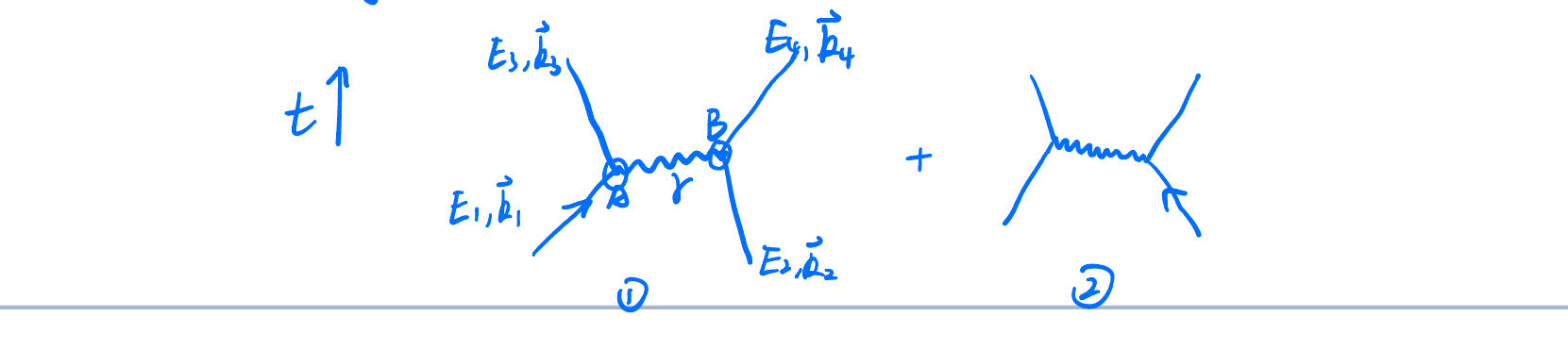
两带电粒子交换光子：

如果要求每个顶点处能量和动量守恒，会遇到“能动量守恒”和“质壳条件”不相容的疑难. 因为确定了两个粒子的初末态能动量，中间的光子就能完全被确定. 这些方程联立起来肯定无解.

所以现在有两个选择：

1. 光子传播时间短，所以在不确定原理范围内，我们允许能动量守恒的微小破坏. 这也是含时微扰论的主要内容.
2. 放弃质壳条件，也就是不认为这个光子实际上存在，它是虚光子. Feynman 选择了这一种方法.
3. 其实还有第三种，就是两个条件都不放弃，解出复数解，这是目前量子场论研究的前沿.

接着第 2 中路线走下去，那么上面的图中光子横着飞行是允许的，同时不区分是由谁发出光子，因为它并不实际存在. 现在一幅图的概率幅正比于光子的质壳条件分之一，因为质壳条件已经被破坏，所以分母不是零：

$$\frac{1}{E^2-\vec{k}^2}$$

Feynman 发现，将上面两个图加起来得到一个 Lorentz 不变的散射幅. 同时再乘上发射光子和吸收光子的概率幅，得到上面一幅图的总概率幅，是$\frac{Q_1Q_2}{E^2-\vec{k}^2}$.

至此光子的传递可以用 Green 函数得到类似于 Coulomb 势的形式：

$$\frac{Q_1Q_2}{r}$$

但是到这一步还是不能说明引力过程中任何粒子的引力荷相同. 在引力子的传递中，发射、吸收概率幅为$\kappa_1$、$\kappa_2$，同时因为自旋 2 的 Green 函数具有某些张量结构导致惯性质量的出现，最后得到的结果应该是

$$\frac{\kappa_1\kappa_2m_1m_2}{r}$$

但是 Feynman 无法给出$\kappa_1=\kappa_2$的解释（所有粒子以同样的强度参与引力作用）.

无质量粒子的极化

为了解释上面讲到的问题，我们考虑无质量粒子的极化 —— 因为上面的问题肯定和引力子的性质有关.

对于有质量的自旋 -1 粒子，在静止系中，$p^\mu=(m,0,0,0)$，三种不同的极化分别是：

$$\epsilon_x^\mu=(0,1,0,0)\,,\epsilon_y^\mu=(0,0,1,0)\,,\epsilon_z^\mu=(0,0,0,1)$$

推广到无质量粒子，两个不同点是：

1. 无质量粒子没有静止系，它们只能以光速飞行. $p^\mu=(p,0,0,p)$.
2. 只有两个独立的极化状态.

第 2 点来源：保持$p^\mu=(p,0,0,p)$不变的 Lorentz 变换构成一个所谓的 ISO(2,1) 群，这个群是二维的旋转变换加上两个平移变换. 这导致光子只有两种极化，光的极化矢量不是 Lorentz 矢量，因此有规范对称$\epsilon_\mu^{(1)}-\epsilon_\mu^{(2)}\propto p^\mu$，视为等同.

推广到 spin - 2 的无质量粒子，则它的自旋张量不是真正的张量，在 Lorentz 变换下会产生一个剩余的张量.

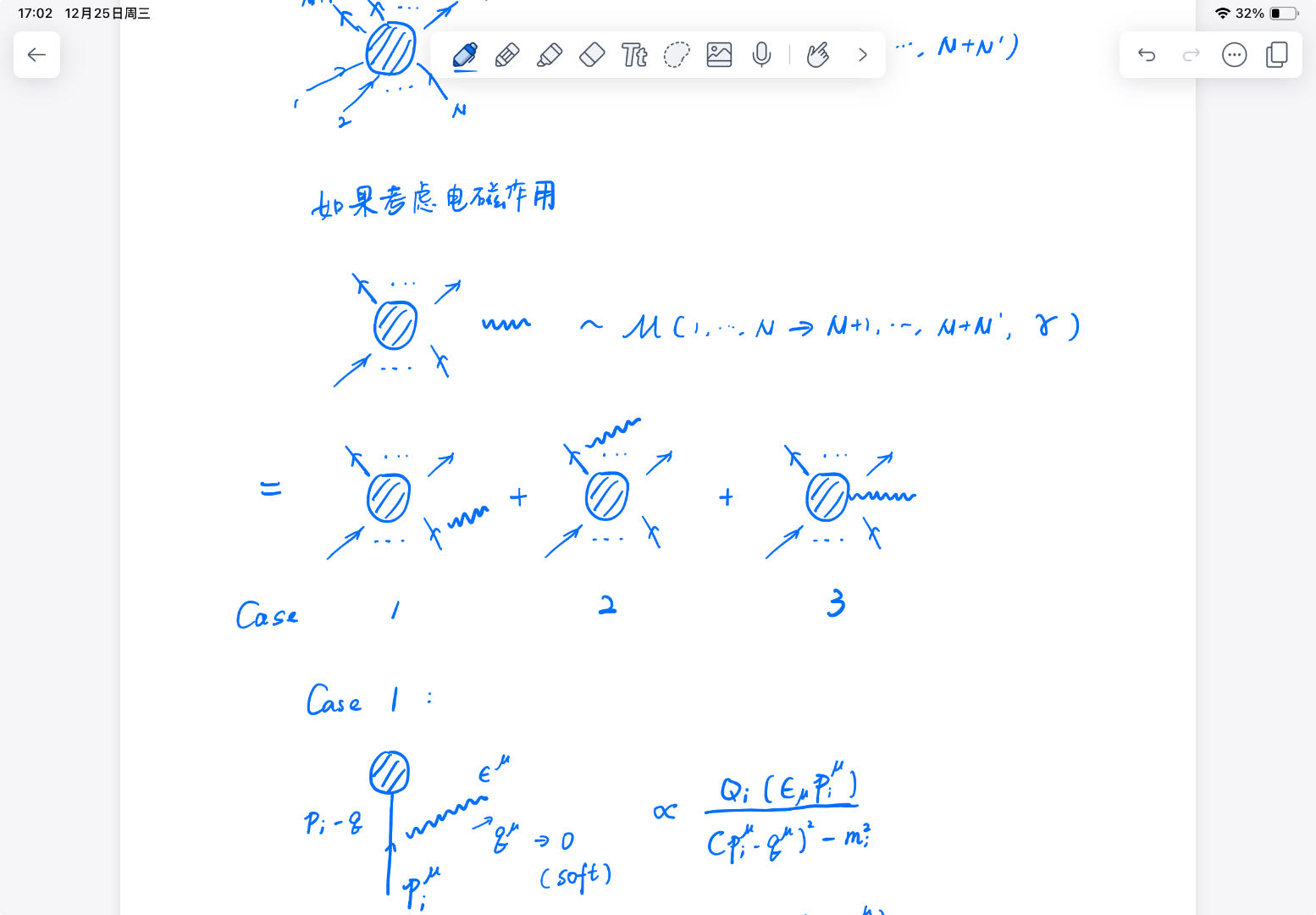
Weinberg 定理

三种情况分别是某过程之前发射光子、某过程之后发射光子和过程中间发射光子，总体合成为某个过程产生一个光子的概率幅.

对于 Case 1：分母是 Green 函数，概率幅正比于

$$\frac{Q_i(\epsilon_\mu p_i^\mu)}{(p_i-q)^2-m^2_i}$$

取$q\to0$的极限，粒子趋于在壳，$p_i\sim m_i$，这个过程的概率幅线性发散，入射概率幅是

$$\frac{Q_i(\epsilon\cdot p_i)}{2(p_i\cdot q)}$$

对于 Case 2：出射粒子动量$p_j$，出射光子动量$q$，对应的散射幅在$q\to0$极限下，散射幅正比于

$$\frac{Q_j(\epsilon\cdot p_j)}{2(p_j\cdot q)}$$

对于 Case 3：发射一个光子动量为$q$，在动量$q\to0$时，整个过程几乎不发生，它是$O(q)$阶的，所以甚至可以忽略这个过程.

我们只要考察正比于$1/q$的发散概率幅，同时将上面三种情况的概率幅叠加，得到：

$$\mathscr{M}=M_0\times\{\sum_{i\in\text{input}}\frac{-Q_i(\epsilon\cdot p_i)}{2p_i\cdot q}+\sum_{j\in\text{output}}\frac{Q_j(\epsilon\cdot p_j)}{2p_j\cdot q}\}$$

因为 Lorentz 变换下，$\epsilon$会多出一个部分（它不是真正的张量），所以上式要保持 Lorentz 协变就必须要求等于零.

所以

$$\sum_{i\in\text{in}}Q_i=\sum_{j\in\text{out}}Q_j$$

这就是电荷守恒.

简单地推广到 spin - 2 的情形，散射幅应该正比于：

$$M_0\times\{-\sum_{i\in\text{in}}\frac{\kappa_i\epsilon_{\mu\nu}p_i^\mu p_j^\nu}{2(p_i\cdot q)}+\sum_{j\in\text{out}}\frac{\kappa_j\epsilon_{\mu\nu}p_j^\mu p_i^\nu}{2(p_j\cdot q)} \}=0$$

所以要求：

$$\sum_{i\in\text{in}}\kappa_ip_i^\mu=\sum_{j\in\text{out}}\kappa_jp_j^\mu\,,\quad\sum_{i\in\text{in}}p_j^\mu=\sum_{j\in\text{out}}p_j^\mu$$

这里有解必须要求$\kappa_i=\kappa_j$，所以只有一种用自旋 - 2 的无质量粒子传递的相互作用，所有粒子以相同的强度参与这种作用. 同时，不存在以自旋$>2$的无质量粒子传递的相互作用，因为方程会无解，这些相互作用不自洽.